基于Markov过程的贮备系统可靠性分析

李浪涛，林凤田，凌 玮

(92351部队，海南三亚 572016)

基于Markov过程的贮备系统可靠性分析

李浪涛，林凤田，凌 玮

(92351部队，海南三亚 572016)

基于Markov过程研究了贮备系统的可靠性，通过建立适用的模型，计算呈现多种状态贮备系统的可靠性参数，得出的结论对维修工程具有一定的技术参考价值。

Markov过程;贮备系统;可靠性

随着现代质量观念的转变，系统的设计和使用更加注重其专门特性［1］，一些连续运行较长时间或者较为重要的设备一般设计采用贮备系统，以提高运行的可靠性。对贮备系统的可靠性分析是判断系统能否达到可靠性指标的依据。本文假设贮备系统各个状态之间的转移服从Markov随机过程，通过建立矩阵方程，运用MATLAB软件进行计算，得出较为精确的工程计算结果。

1 基于Markov过程的贮备系统可靠性分析模型

假设互为备用的2台设备A和B，其组成的贮备系统的工作状态有5种:状态0，1，2，3，4。状态0－A工作，B备用;状态1－A备用，B工作;状态2－A工作，B故障;状态3－A故障，B工作;状态4－A和B都故障。系统在t时刻处于状态0，1，2，3，4的概率分别为:P0(t)，P1(t)，P2(t)，P3(t)，P4(t)。假设设备A和B工作时的故障率为λ0，备用时的故障率为λ1，维修率为μ，系统状态转移如图1所示。

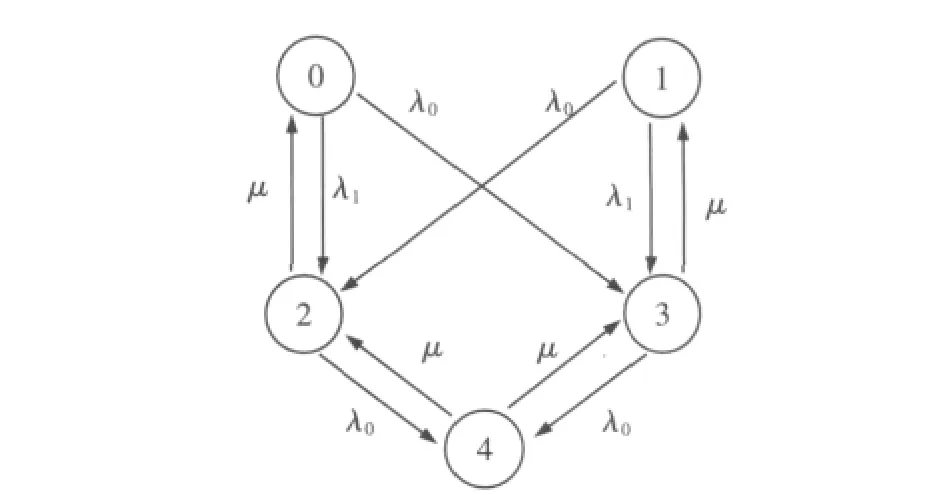
图1 贮备系统的状态转移图

假设各状态之间的转移服从Markov过程，由Markov过程的定义［2］，其最大的特点是无后效性，则状态转移方程为:

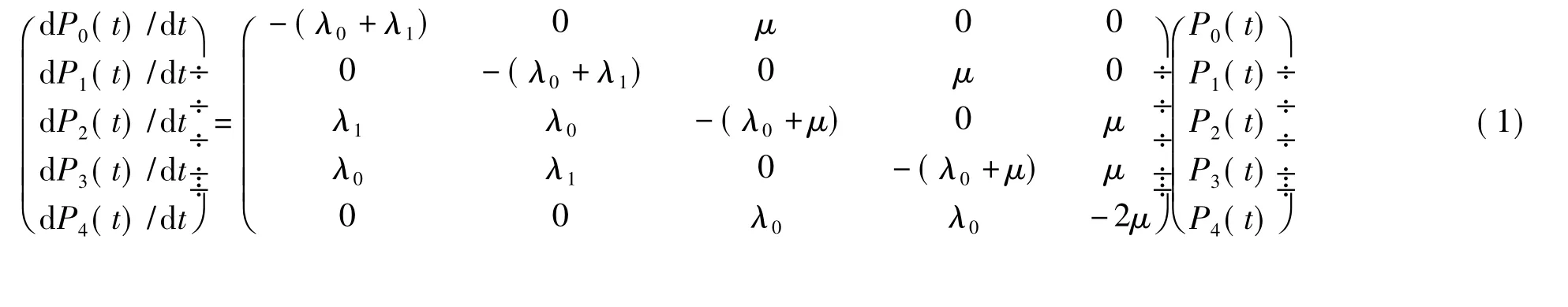
定义:

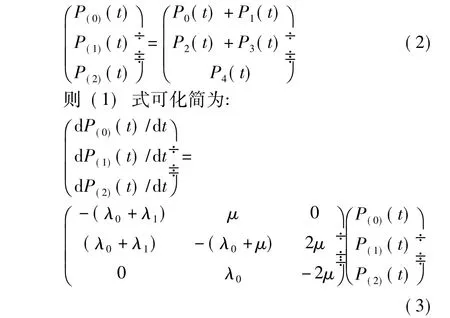
设初始条件为:

由系统状态的归一性知:

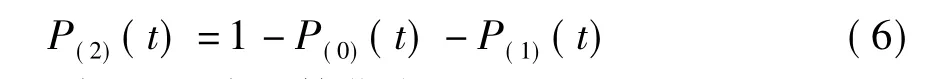
则 (3)式可简化为:

由Laplace变换可得:

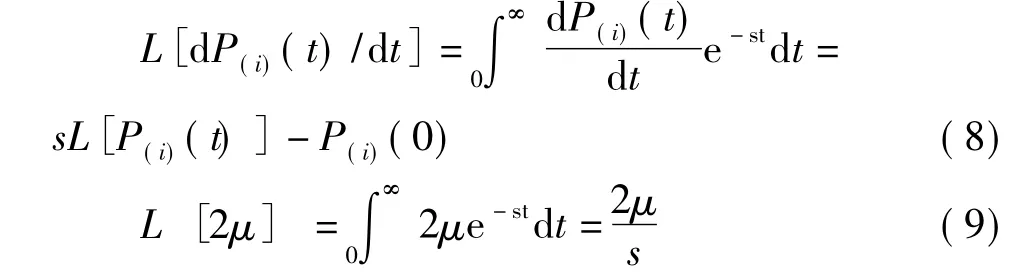
对 (7)式Laplace变换并化简，得:

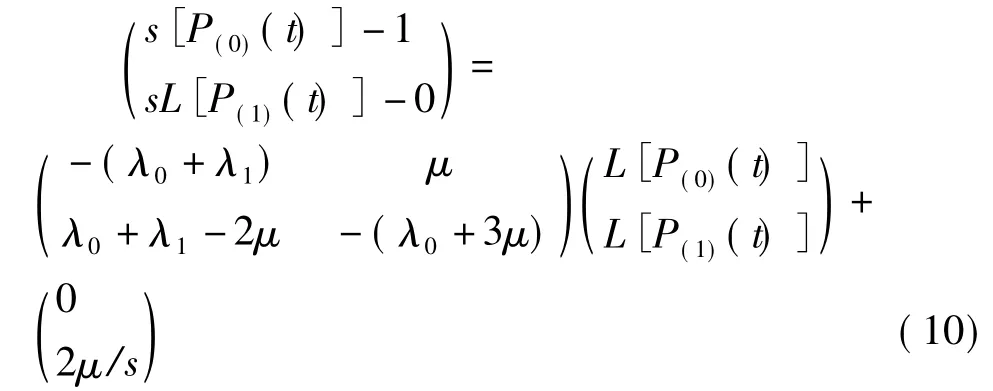
进一步化简 (10)式，得:

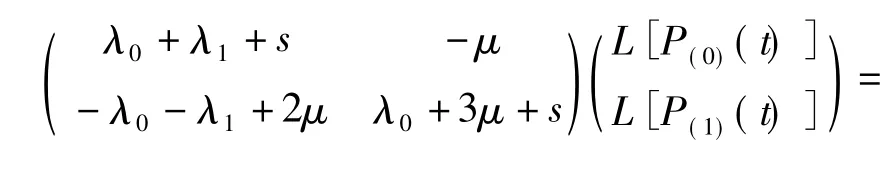
根据式 (11)，计算出 L［P(0)(t)］、L［P(1)(t)］，分别对其 Laplace逆变换，求出 P(0)(t)、P(1)(t)，计算过程可由MATLAB软件完成。根据5种状态的划分及P(0)(t)、P(1)(t)、P(2)(t)的定义知，P(2)(t)表征此贮备系统的故障率，P(0)(t)+P(1)(t)表征贮备系统的可靠度。

2 典型算例

设某重要水源供应系统由2台互为备用的水泵A、B组成，A和B工作时的故障率λ0=2×10－4h－1，备用时的故障率 λ1=10－4h－1，当设备维修率分别为 μ1=10－3h－1、μ2=2 ×10－3h－1、μ3=3×10－3h－1时，计算此系统运行 100 h，500 h，1 000 h，∞ (无穷大) 的可靠度R1、R2、R3。

将 λ0、 λ1、μ ( 指 μ1、 μ2、 μ3) 代 入 式(11)，经计算可得 P(0)(t)、P(1)(t)，根据 R=P(0)(t)+P(1)(t)计算，结果如表1。

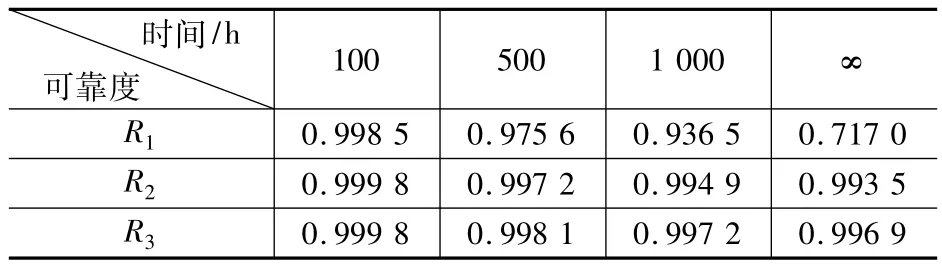
表1 贮备系统运行的可靠度

3 结束语

由上述计算结果可知，当时间趋于无穷大时，设备的故障率总是趋于一个稳定的概率，随着维修率的提高，设备的故障率有明显的降低。因此提高维修人员的素质和维修质量对于提高设备可靠性，延长系统稳定运行时间十分重要。

本文的计算主要针对二元件组成的系统，该模型也可运用于多元件组成的系统［3］。本文将贮备系统的状态划分为5种，因此建立的模型可用于多状态可靠性分析。

［1］曾声奎，赵廷弟，张建国，等.系统可靠性设计分析教程［M］.北京:北京航空航天大学出版社，2001.

［2］汪荣鑫.随机过程 ［M］.2版.西安:西安交通大学出版社，2006.

［3］陆志峰，周家启，阳少华，等.多元件备用系统可靠性计算研究 ［J］.中国电机工程学报，2002，22(6):52－55.

Based on Markov procession，the reliability of standby system is studied.By constructing the applicable mode，the reliability parameters of the standby system that takes on multi-state are calculated.The conclusion has been the technical reference value for the maintenance project.

Markov procession;standby system;reliability

TB114.3

A

1001－8328(2012)06－0045－02

李浪涛 (1979-)，男，陕西蓝田人，工程师，硕士，现从事维修技术管理工作。

2012－05－09