基于类别多核局部判别嵌入的人脸识别
王永茂,徐正光,吴金霞
(1.北京科技大学自动化学院,北京100083;2.河南理工大学 计算机科学与技术学院,河南焦作454003)
0 引言
为了缓解人脸识别中存在的维数灾难问题,需要进行有效的降维.主元成分分析(PCA,Principle Component Analysis)[1]是最流行的降维方法之一,但其本质是线性的,不能很好地描述人脸图像中诸如光照、表情和姿态等复杂的非线性变化.基于流形的降维方法是近年来兴起的一类降维方法,其中代表性的算法有等距映射(ISOMAP)[2]、局部线性嵌入(LLE,Locally Linear Embedding)[3]和拉普拉斯映射(LE,Laplacian Eigenmap)[4],它们能够很好学习到非线性流形结构,但是基于流形的降维方法的一大缺陷是不能直接映射新的测试点,为了解决这一问题,许多学者先后提出局部保形投影(LPP,Locality Preserving Projection)[5]、近邻保形嵌入(NPE,Neighborhood Preserving Embedding)[6]等线性降维算法,它们分别为LE算法与LLE算法的线性逼近.
上述提到的线性或非线性降维方法的设计初衷并不是应用于分类,而Fisher判别分析(FDA,Fisher Discriminant Anaysis)[7]得到的最佳映射子空间具有较好的鉴别能力,因此对于分类任务能够起到较好的效果.为了保持数据的流形结构,研究者提出了一类既考虑类别信息又考虑邻域结构信息的降维方法[8-13],这些降维方法既具有较好的鉴别能力又能很好保持数据的近邻特性.局部判别分析(LDE,Local Discrimiant Embedding)[8]是其典型代表.然而,LDE本质上仍然是线性方法,不能够很好揭示数据复杂的非线性结构,许多学者提出利用非线性核技巧在维数很高的空间内求解子空间的核局部判别嵌入(KLDE,Kernel Local Discriminant Embedding)降维方法[8,14].该方法将输入的数据空间转换到一个高维空间,其映射关系在全局范围内定义,在映射的过程中改变了数据分布,不能够很好保持数据的几何结构.为解决这一问题,笔者提出一种基于类别多核局部判别嵌入算法(LMKLDE,Label Mulitple Kernel Local Discrimiant Embedding),首先针对给定样本数据的类别信息,定义类别局部核函数,形成多核,接着将不同的局部核函数进行线性组合,作为最终的核函数引入到LDE算法中,得到了LMKLDE算法.
1 LDE
假设有一数据集 X={(x1,l1),(x2,l2),…,(xN,lN)},xi是一个D维向量,N为样本的个数,li∈ L={1,2,…,m} 为xi的类别标签,L是类别标签集,m为类别总数.LDE算法的目的就是寻找一投影矩阵V,得到X的低维嵌入Y={y1,y2,…,yN},使得Y=VTX,yi是一个d维向量,且d<D.
根据图框架理论[9],LDE算法构造两个近邻图:(1)描述类内紧密性的近邻图Gw(固有图),图中每个样本只与同类别的k1个近邻点相连,Nw(xi)表示样本xi同类别的k1个近邻点;2)描述类间分离性的近邻图Gp(惩罚图):图中每个样本只与不同类别的k2个近邻相连,Np(xi)表示样本xi不同类别的k2个近邻点.
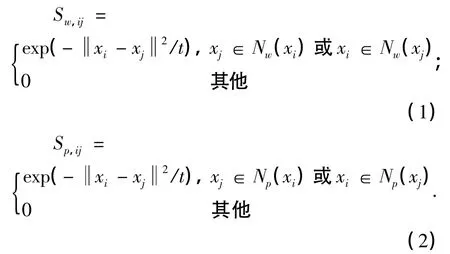
计算近邻图Gw和Gp的权值矩阵Sw和Sp,其值为
为了保证xi和xj在相距很近且具有相同类别标记时,其低维嵌入yi和yj相距也很近;xi和xj在相距很近但具有不同类别标记时,yi和yj相距很远.LDE算法的目标函数定义为
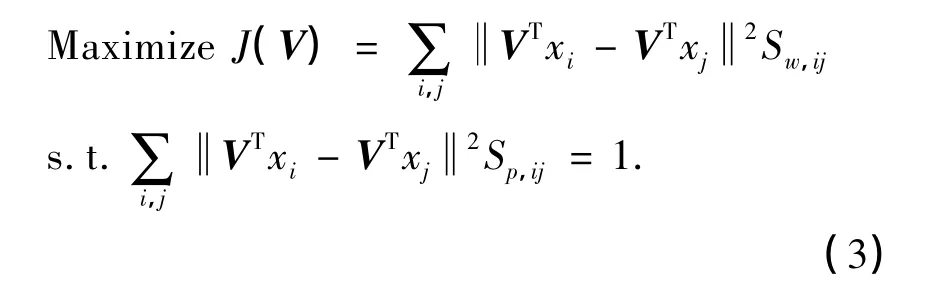
经过推导,LDE目标函数变为

其中Lw=Dw-Sw和Lp=Dp-Sp为拉普拉斯矩阵,Dw和Dp为对角矩阵,其值为权值矩阵Sw和Sp每一列(或行)数据之和,即
式(5)进行广义特征分解的前d个最大特征值对应的特征向量组成了LDE的基向量V=[v1,v2,…,vd].
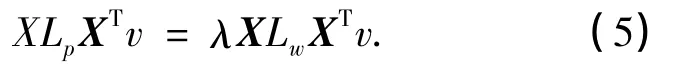
2 类别多核函数
核函数提供了一种数据相似度度量方法,对于两个样本x和z,Φ(x)和Φ(z)是样本x和z的高维非线性映射,则Φ(x)和Φ(z)的点积可用x和z的核函数表示,即
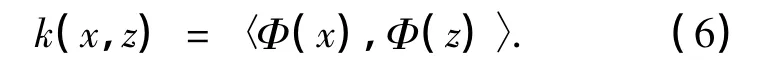
下面给出类别多核函数的构造.
对于样本x,求其到类别c中心的矢量xc,其值为
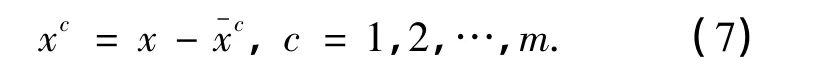
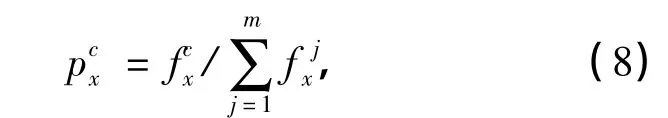
定义基于每一个类别的局部核,即

将不同的局部核函数进行线性组合,得到最终的核函数,即

3 LMKLDE
将类别多核函数应用到LDE算法,以处理非线性结构数据,得到LMKLDE算法.
3.1 LMKLDE的求解过程
假设Φ为一非线性映射函数,将样本X映射到希尔伯特空间内[15],得到 Φ(X)= [Φ(x1),Φ(x2),…,Φ(xN)].于是,希尔伯特空间中的广义特征问题表示如下:
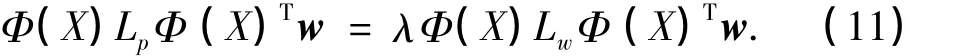
由于上式的特征向量 w为 Φ(x1),Φ(x2),…,Φ(xN)的线性组合,故w可表示如下:
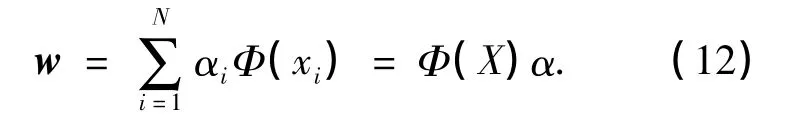
经过简单的变换,式(11)变为
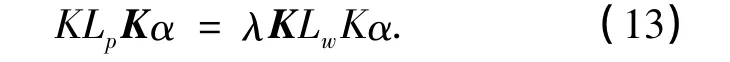
其中:K为核矩阵,其值由式(10)定义的类别多核函数决定.求解式(13)对应的广义特征向量,得到d个特征向量 α1,α2,…,αd,分别对应于d 个最大的特征值.那么对于一个测试样本x,它在特征向量wk上的投影为
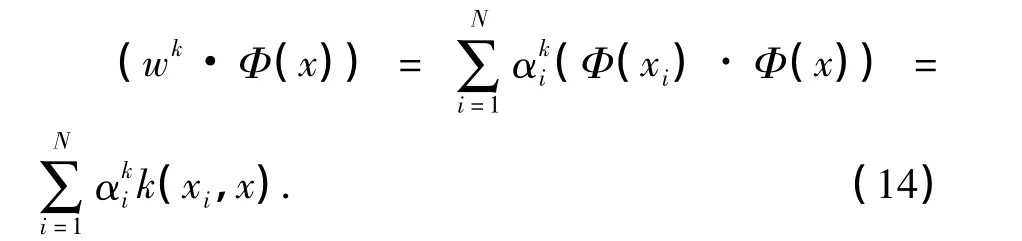
3.2 LMKLDE的时间复杂度分析
KLDE算法的时间复杂度主要有以下3个方面决定:(1)近邻点的搜索;(2)核函数的构造;(3)广义特征向量问题的求解.
近邻点的搜索的时间复杂度为O((D+k1+k2)N2),DN2代表计算任意两个样本距离的时间复杂度,k1N2代表寻找同类别的k1个近邻点的时间复杂度,k2N2代表寻找不同类别的k2个近邻点的时间复杂度.核函数的构造的时间复杂度为O(DN2).求解广义特征向量的时间复杂度为O(N3).
LMKLDE与KLDE区别仅在于核函数的构造,核函数构造的时间复杂度为O(mDn2),大于KLDE的核函数构造的时间复杂度O(Dn2),因此,LMKLDE的执行时间要比KLDE长,当m≪D时,其执行时间差别不大.
4 实验设计和结果
为了验证算法的有效性,分别在ORL和Yale人脸库上进行实验对比.实验中比较了LMKLDE与 PCA,FDA,LDE以及 KLDE的识别率,在KLDE,LMKLDE方法中,核函数采用线性核函数,k(x,z)=(1+xTz)d,d=1; 以及高斯核函数,k(x,z)=exp(- x - z2/2σ2),σ =1,对于所有方法,均采用欧式距离度量下的最近邻分类器完成最终分类.
ORL人脸库是由英国剑桥大学建立,共有40个人,每人10张图像,共有400张人脸图像,图像的面部表情和面部细节有着不同程度的变化,人脸姿势也有相当的程度变化,比较充分地反映了同一人不同人脸图像的变化和差异.图1是ORL人脸库的部分样本.Yale人脸库由美国耶鲁大学建立,包含15个人,每人11张图像,共有165张人脸图像,主要包括光照条件的变化、表情的变化及有无眼睛修饰等.图2是Yale人脸库的部分样本.实验使用的人脸图像经剪切后大小均为32×32,然后将两个人脸库中的每个图像进行标准化.
在对ORL和Yale人脸库进行实验时,从每类人脸图像中随机选取i(i=2,3,4)张图像作为训练集,剩余的图像作为测试集,重复进行10次,共获得10对不同的训练集和测试集,分别以2Train,3Train和4Train表示,最后取平均值作为识别结果.表1和表2给出了ORL和Yale人脸库的平均最高识别率及其对应的子空间的维数,其中(L)为采用线性核函数的识别结果,(G)为采用高斯核函数的识别结果.
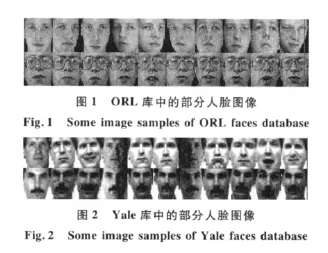

表1 ORL人脸数据库上的实验结果比较Tab.1 The experiment result on ORL database

表2 Yale人脸数据库上的实验结果比较Tab.2 The experiment result on Yale database
从上面的实验可以看出:
(1)FDA考虑样本的类别信息,识别率高于PCA方法;
(2)LDE既考虑样本的类别信息又考虑样本之间的近邻关系,对于非线性流形结构有一定的保持作用,其识别率要高于FDA;
(3)KLDE以及LMKLDE在核空间提取图像的高阶非线性信息,其识别率高于其他方法,但KLDE方法的核函数在全局范围内定义,而LMKLDE方法的核函数是类别局部核函数的线性组合,考虑了样本的几何分布,因此LMKLDE的识别率高于KLDE.
5 结论
笔者在LDE算法的基础上提出了一种基于类别多核局部判别嵌入的人脸识别算法.算法通过将不同类别的局部核函数进行线性组合所得到最终的核函数引入到LDE算法中,得到LMKLDE算法,能够较好的保持数据的几何结构.在ORL和Yale人脸库上的实验结果表明,在姿态、光照和表情等变化的情况下,该算法都具有良好的性能.
[1]TURK M,PENTLAND A.Eigenfaces for recognition[J].Journal of Cognitive Neuroscience,1991,3(1):72-86.
[2]TENENBAUM J B,SILVA V,LANGFORD J C.A global geometric framework for nonlinear dimensionality reduction[J].Science,2000,290(12):2319 -2323.
[3]ROWEIS S T,SAUL L K.Nonlinear dimensionality reduction by locally linear embedding [J].Science,2000,290(12):2323 -2326.
[4]BELKIN M,NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation [J].Neural Computation,2003,15(6):1373 -1396.
[5]HE Xiao-fei,YAN Shui-cheng.Face recognition using laplacianfaces[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2005,27(3):328 -340.
[6]HE Xiao-fei,CAI Deng,YAN Shui-cheng,et al.Neighborhood preserving embedding[C]//Tenth IEEE International Conference on Computer Vision.Piscataway:Institute of Electrical and Electronics Engineers Inc.,2005:1208 -1213.
[7]BELHUMEUR P N,HESPANHA J P,KRIEGMAN D J.Eigenfaces vs.fisherfaces:Recognition using class specific linear projection[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1997,19(7):711 -720.
[8]CHEN HW,CHANG HW,LIU TL.Local Discriminant Embedding and Its Variants[C]//2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Pis cataway:Institute of Electrical and Electronics Engineers computer Society,2005:816-853.
[9]YAN Shui-cheng,XU Dang,ZHANG Ben-yu,et al.Graph Embedding and Extensions:A general framework for dimensionality reduction[J].IEEE transaction on Pattern Analysis and Machine Intelligence,2007,29(1):40 -51.
[10]王超,王士同.最大间距准则与局部保持结合的特征提取方法[J].计算机工程,2009,35(14):209-211.
[11]张召,业宁,业巧林.局部保持多投影向量Fisher判别分析算法[J].计算机学报,2010,33(5):385-396.
[12]魏莱,王守觉,徐菲菲,等.近邻边界Fisher判别分析[J].电子与信息学报,2009,31(3):509 -513.
[13]CAI Hong-ping,KRYSTIAN M,JIRI M.Learning linear discrimiant projection for dimensionality reduction of image descriptors[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,2011,33(2):338 -351.
[14]王庆军,张汝波,潘海为.基于核正交局部判别嵌入的人脸识别[J].光电子激光,2010,21(9):1386-1389.
[15]申中华,潘永惠,王士同.有监督的局部保留投影降维算法[J].模式识别与人工智能,2008,21(2):233 -239.

