二维大地电磁正演中无网格算法研究
苏 洲,胡文宝,朱 毅 (油气资源与勘探技术教育部重点实验室(长江大学),湖北荆州434023)
二维大地电磁正演中无网格算法研究
苏 洲,胡文宝,朱 毅 (油气资源与勘探技术教育部重点实验室(长江大学),湖北荆州434023)
无网格法是近几年来发展的一种新的基于变分原理的数值计算方法,由于在计算形函数中不需要划分网格,在力学、电磁学等领域得到了广泛的研究。基于无网格法在大地电磁勘探正演中的应用进行了研究,首先对无网格法的基本原理进行了阐述,并利用广义变分原理推导出了相应的离散方程,编制了相应的程序。最后通过理论模型的计算结果检验了该算法的正确性。
无网格法;大地电磁法;移动最小二乘拟合(MLS);有限元法
大地电磁测深法(MT)是一种以岩石的电性差异为基础和前提,利用天然交变电磁场研究地球电性结构的勘探方法[1~3]。在解决MT正演问题时,有限差分法[4]和有限元法[5,6]是主要的数值计算方法;尽管这些方法取得了巨大成功,但是这些方法都是基于网格的数值计算方法,也有其自身的局限性[7],如网格部分计算成本高、计算精度依赖于单元剖分的形状和大小等。产生上述问题的一个主要原因是这些方法都是基于网格剖分来建立离散系统方程的,为克服这些困难,无网格方法(Meshless)作为有限元法(FEM)的一种重要补充具有重要的研究意义。
无网格法(Meshless)是近10年来兴起的一种数值计算方法[7],它是在有限元法的基础上发展起来的,但是不同于有限元;无网格法的近似函数是建立在一系列离散节点上的,然后在这些节点上利用形函数求出其近似值,代入相应的变分问题得到系统方程。
无网格法已在力学[8]、油藏渗流问题[9]、电磁学[10]等领域得到了广泛的研究,然而在求解地球物理正演问题中的理论和应用研究鲜少出现。为此,笔者利用无网格法对二维MT正演做了相关研究。首先从麦克斯韦方程组出发,推导出二维介质中边值所对应的广义变分问题;然后用节点离散求解区域,得到建立在离散节点上的无网格形函数,求解变分问题得到边值问题对应的离散方程,解方程后代入视电阻率计算公式计算地面上待求点的视电阻率。

图1 理论模型
1 边值问题及其变分问题
大地电磁场可以看作是从高空垂直入射到地面的平面电磁波[1],基于这种假设可以推导二维情况下大地电磁测深法所对应的边值问题[2],如图1所示:

式(1)所对应的变分问题为求如下泛函I(u)的极值:

2 二维大地电磁正演中无网格算法研究
微分方程及其边界条件与变分问题是等价的,因而求解微分方程可以等价为求解变分问题[11]。其基本思想为:求解变分问题的最终目的是得到在求解区域中N个离散节点的值,假设待求函数在N个节点有准确值,任意点的函数值可以通过形函数来表示,将其代入变分问题中,求泛函极小即可得到关于N个节点值的方程。因而在求解变分问题时,首先要构造形函数。
不同的方法构造的形函数不同[12]:有限元法中,其形函数是通过单元的一组固定节点利用插值技术构造的;而在无网格法中,任意点的场变量是由该点局部支持域中的一组场节点近似表示的。该次研究采用移动最小二乘近似法来构造无网格形函数。设求解域Ω内,待求场函数u在N个节点处的场值ui=u(xi)(i=1,2,…,N)是已知的,基于这些已知节点构造待求函数u在求解域Ω上的近似uh(x),设表达式为:

式中,x为计算点为x的邻域中的结点;a(x)为待求系数为基函数;I表示基函数的个数。在求解域Ω内,N个节点处定义权函数。笔者分别对三次和四次样条权函数进行研究。
设计算点x的定义域Ωx包括N个节点,近似函数在节点=xi处的加权离散平方和为:J=
本质边界条件在式(2)中并未得到满足,因而采用广义变分原理[12]将场函数满足的本质边界条件引入泛函,使有约束条件的变分问题变成无约束条件的变分问题。构造修正泛函常用的方法有拉格朗日乘子法和罚函数法[12]。该次研究采用拉格朗日乘子法得到修正泛函I*(u,珔λ):

在有限元中,求解域Ω被离散成一系列单元,积分问题可以转化为对各单元积分的和。在无网格法中,求解域Ω是用节点离散表示的,不存在网格。因此在无网格法中需要特殊的积分方案。用规则网格覆盖求解域Ω,将对求解域Ω的积分转化为对各规则单元的积分之和,在每个格子中使用高斯积分[12],如图2所示。通过上述方法得到式(6),求解得各节点处的值,其值为各节点的HY,EY值,代入视电阻率计算公式[2]即可。
3 数值模拟计算
对于上述求解过程,利用Matlab编写了二维MT正演的无网格算法程序,并与有限元方法做了对比研究,根据图3所示模型进行了计算。结果见图4~7。

图2 无网格法中背景网格单元积分点及其节点圆形影响域

图3 理论模型

图4 TE、TM极化模式下0点电阻率对比图
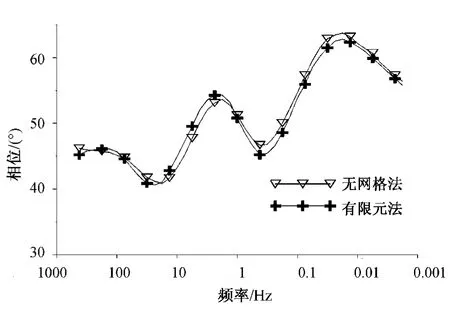
图5 TE极化极化模式下0点相位对比图
由图4、5可见,无网格法和有限元法有相似的计算结果,证明了二维情况下算法的正确性;由图6、7可见,二维等值线可以很好地反映异常体特征。此外,由于无网格法形函数构造不需要网格信息,因而对于求解区域节点的设置没有限制,相对于有限元法和有限差分法简单了许多;在计算过程中发现权函数和节点影响域对计算精度有着直接的影响;在计算效率方面,由于无网格法需要在每个积分点重新计算其邻域中所包含的节点数,需要更多的节点信息,因而需要更长的计算时间。现有的资料中已经出现过无网格并行算法[13],为了将无网格法用于实际,研究地球物理无网格算法的并行计算将是今后研究的方向之一。

图6 TM极化模式下视电阻率和相位等值线图
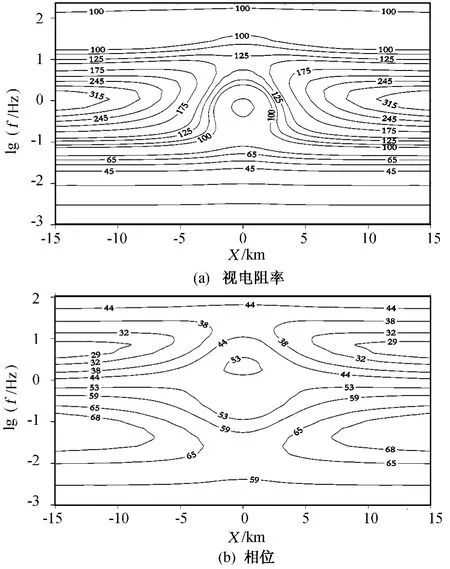
图7 TE极化模式下视电阻率和相位等值线图
4 结 论
1)无网格数据结构简单,只需要节点信息,脱离了网格的限制,计算结果具有高阶连续性。
2)在构造无网格形函数时,权函数的选择和节点影响域对计算结果有着较大的影响,对于具体模型计算前,要根据数值试验确定上述参数,笔者采用4次样条权函数,影响域权重取2.3。
3)由于无网格法在每个计算点处要重新计算相应的形函数值,因而其计算复杂度较高。
[1]朴化荣.电磁测深法原理[M].北京:地质出版社,1990.1~50.
[2]徐世浙.地球物理中的有限单元法[M].北京:科学出版社,1994.50~164.
[3]胡建德.电法勘探中的数学模型[J].数学的实践与认识,2004,34(2):26~30.
[4]谭捍东,余钦范,John Booker,等.大地电磁法三维交错采样有限差分数值模拟[J].地球物理学报,2003,46(5):705~710.
[5]陈乐寿.有限元法在大地电磁测深正演计算中的应用与改进[J].石油物探,1981,20(3):84~103.
[6]陈小斌,张翔,胡文宝.有限元直接迭代算法在MT二维正演计算中的应用[J].石油地球物理勘探,2000,35(4):487~496.
[7]陶文铨,吴学红,戴艳俊.无网格数值求解方法[J].中国机电工程学报,2010,30(5):1~10.
[8]张雄,刘岩.无网格法[M].北京:清华大学出版社,2004.14~103.
[9]李玉坤,姚军,黄朝琴,等.油藏渗流问题的无网格法分析[J].中国石油大学学报(自然科学版),2003,31(2):95~104.
[10]茅昕光,林鹤云.电磁场数值分析的无单元Galerkin方法[J].东南大学学报,2003,33(1):31~35.
[11]老大中.变分法基础[M].北京:国防工业出版社,2007.11~104.
[12]Liu G R,Gu Y T.An introduction to meshfree methods and their programming[M].Berlin:Springer,2005.54~114.
[13]曾清红.无网格数值模拟的并行算法及并行实现研究[D].合肥:中国科学技术大学,2006.
[编辑] 龙 舟
87 Meshfree Method Used in Two-dimensional Magnetotelluric Forwarding
SU Zhou,HU Wen-bao,ZHU Yi
(AuthorsAddress:Key Laboratory of Exploration Technologies for Oil and Gas Resources(Yangtze University),Ministry of Education,Jingzhou434023,Hubei,China)
As a new numerical computational method based on the principle of variation,meshfree methods has maintained a rapid development in recently years.It has widely applied in studying the problem of the mechanics and electromagnetics because of avoiding the onerous mesh generation.The application of meshfree method in magnetotelluric forwarding was studied.First,the fundamental principle of meshfree method was described and the particular meshless calculating formulas were deduced through the generalized variation principle.The program is verified by comparison with the analytic response of a symmetrical ladders model and with finite difference results of laterally inhomogeneous model.
meshfree method;magnetotelluric;moving least-square method;FEM
book=112,ebook=112
P631.325
A
1000-9752(2012)05-0087-04
2012-02-10
国家“973”规划项目(2007CB209607);国家自然科学基金项目(40727001)。
苏洲(1986-),男,2009年大学毕业,硕士生,现主要从事电磁测深正演方法的研究工作。

