Contourlet变换在图像降噪中的应用*

蔡文涛

（中北大学仪器科学与动态测试教育部重点实验室，山西太原 030051）

在过去的十年中，小波已经被广泛地用于各个领域中。在图像处理领域，小波变换被广泛用于图像压缩，图像降噪，特征提取和水印领域等等［1］。因为传统的小波有着一些缺点，所以我们提出了Contourlet变换。

本论文将BayesShrink阈值和WindowShrink阈值融于Contourlet变换当中，这个新的图像降噪方法实现了可以更好地逼近非线性高维函数的多尺度几何变换方法，这样也可以更加方便的在计算机上模拟。从仿真结果来看，这个方法比小波变换和曲波变换在一些方面更有优势。

1 Contourlet变换的离散实现

Contourlet变换的基本思想是首先用多尺度分解捕捉到奇异点边缘，然后，保证奇异点的位置和信息量的位置接近。1983年，Contourlet变换已被伯尔和阿德尔森用于拉普拉斯金字塔的图像多分辨率。

1.1 金字塔滤波器

电源模块用LM1117 3.3 V芯片提供输出电压为4.5 V～10 V来保证最大输出电流800 mA。

拉普拉斯金字塔分解是一种有效的方式，可以来实现图像的多分辨率分析，每个级别的金字塔滤波器分解会产生下一个低通采样的图像和预测图像之间的差分图像，从而逐步滤波得到多分辨率分解的图，正如在图1中示出。

图1 拉普拉斯金字塔的分解与重构

1.2 方向滤波器

班贝格和史密斯于1992年构建了一个二维方向滤波器组，它通过对二进制树频域的分解，产生一系列的子带，而且它可以被使用相同数量的信道结构来代替。

关于分解方法现在有了一种新的方法，这个简单的DFB包括两个模块:第一个是梅花滤波器组的两个通道，它分离成垂直和水平方向的频域;另一个是并行操作，它的功能是重新排列图像样本。为了让金字塔的过滤器和方向过滤器一起实现contourlet变换，金字塔分解没有方向，方向滤波器无法实现多尺度分解，把它们放在一起就可以很好地描述图像特征。

1.3 Contourlet变换的理论依据

Contourlet变换和小波变换是不同的，它不再按照“XX”，“XY”和“YY”方向分解，寿命长，但要控制角度，根据角度分解，n表示一系列的分解值。这个分解的优点是:分解并不仅仅局限于三个方向，而是更多，该系列的分解是越高，将会包含图像更多的图像细节。此外，Contourlet变换后，还将获得一系列的Contourlet变换系数，提供有用的信息相结合的图像系数是非常大的，而结合噪声的图像的系数是非常小的，Contourlet变换滤波器组合图如图2所示:

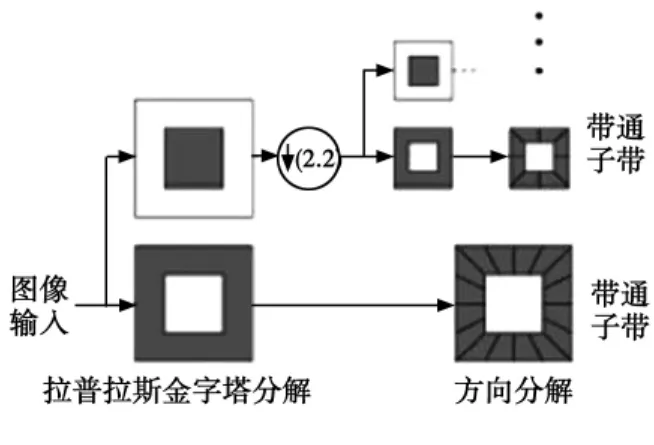
图2 controulet变换滤波器组结构

2 BayesShrink阈值和WindowShrink阈值结合

阈值降噪是图像去噪最常用的方法，其基本思想是将原始图像作出相应的转变，通过一个合适的阈值，使噪声点和信号点的变换系数区分，然后通过逆变换重建图像，从而实现去除原始图像的噪声的目的。

2.1 WindowShrink 阈值去噪［2］

WindowShrink图像去噪的方法是非常重要的在小波理论。通过小波参数的自适应处理，它可以实现去除噪声的目标，本文把这理论应用于Contourlet系数进行移除噪声，具体如下:

设di，j是 Contourlet变换降噪的系数，每个di，j经过以下变换:

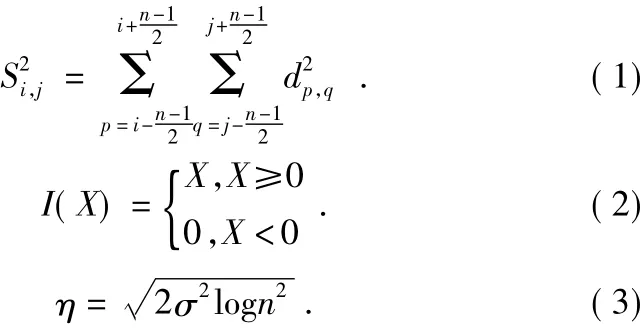
降噪之后的Contourlet系数是:

2.2 BayesShrink阈值去噪

基于贝叶斯的估计可以得到小波阈值函数的去噪方法［3］，下面的方法是 BayesShrink阈值的计算方法，Bayes-Shrink方法得到贝叶斯准则下，贝叶斯最理想的条件下获得的阈值设置为:

在他们之间，rBayes是贝叶斯冒险函数，这是非常难以解决的解析表达式。所以通常模拟情况下我们用数值方法计算近似解［4］:

σ是图像降噪的标准偏差，WindowShrink阈值去噪的系数是:

δ2n是高斯噪声的方差，δ是无噪声信号的标准方差。

x我们定义σ2D是噪声图像的方差，σ2是噪声图像方差，σ2x是初始的图像方差，而

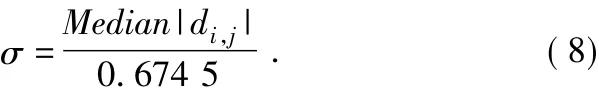
其中Median|di，j|是变换后的最低的频率系数的平均，

原始图像的方差是:

2.3 多阈值去噪

尽管该方法使用一个自适应的方式，噪声WindowShrink阈值去噪图像必须是高斯噪声，我们首先应该知道方差，虽然BayesShrink阈值去噪估计噪声的方差，它不能处理好噪声。本文提出了与BayesShrink阈值相结合的多阈值去噪，我们通过使用BayesShrink理论估计方差为σ2x的原始图象，然后我们用σ2x代替σ2计算。

3 仿真结果

图3是噪声方差为40的图像和处理对比度。

图3 仿真结果

4 结论

在本文中，我们将具有多分辨率和多方位的特点的Contourlet变换分解，通过比较小波变换的理论得出Contourlet变换，本文强调阈值去噪，并提出了一种新的多阈值图像去噪方法。实验结果表明，这种图像去噪方法比小波变换和单独的阈值去噪效果是更好的，而且这种方法简单又计算速度快。

［1］郑治真.小波变换及其MATLAB工具的应用［M］.北京:地震出版社，2010.

［2］刘贵忠，邸双辆.小波分析及应用［M］.西安:西安电子科技大学出版社，2009.

［3］潘泉，张磊.小波滤波方法及应用［M］.北京:清华大学出版社，2011.

［4］杨福生.小波变换的工程分析与应用［M］.北京:科学出版社，2006.