一种塑料模型沙运动特性试验

唐立模，刘全帅，韩柯尧，肖 洋

(1.河海大学水文水资源及水利工程科学国家重点实验室，江苏南京 210098;2.河海大学水利水电学院，江苏南京 210098)

一种塑料模型沙运动特性试验

唐立模1，2，刘全帅2，韩柯尧2，肖 洋1，2

(1.河海大学水文水资源及水利工程科学国家重点实验室，江苏南京 210098;2.河海大学水利水电学院，江苏南京 210098)

对一种复合塑料模型沙的水下休止角、群体沉速、起动流速等运动特性进行了试验研究:使模型沙在静水中自然落淤成丘，通过几何关系可得水下休止角;将沙样按粒径分组进行单颗粒沉速试验，统计平均后再按质量加权得到模型沙群体沉速;在玻璃水槽中对5种水深下的泥沙起动流速进行了测量及经验公式验证。试验结果表明:该模型沙水下休止角为28.4°，较传统塑料沙、水下休止角范围大，具有较好的水下成形特性;对于该模型沙，其单颗粒沉速用W.W.Rubey公式计算精度较高，但群体沉速用中值粒径进行经验计算则精度不够，合理的代表粒径有待进一步研究;起动流速比传统塑料沙大，这与水下休止角试验是相符的，通过调整沙莫夫系数K，沙莫夫公式可较好地表述个别起动和少量起动的情况，大量起动时则不够精确。

塑料模型沙;水下休止角;群体沉速;起动流速

在航道整治、桥梁枢纽等工程的论证阶段，动床模型试验是一种常用的研究手段。模型沙的合理选择是保证模型与原型泥沙运动及河床冲於相似的关键，会影响模型试验结果的可靠性［1］。

水下休止角是反映泥沙运动特性的一个重要指标。对动床模型试验而言，模型沙与天然沙水下休止角的不相似，有可能给边坡上泥沙颗粒的起动相似和河床变形相似带来很大影响。张红武等［2］对天然沙、塑料沙等多种材料沙样的水下休止角进行了研究，得出其各自的变化规律。对于塑料均匀沙样，当粒径d=0.2～0.8 mm时，水下休止角稳定在23.5°左右;而d＞0.8 mm时，休止角则呈现出随粒径增大而减小的趋势。金腊华等［3］也做了相关研究，给出了均匀沙和非均匀沙水下休止角的计算公式，认为由于小颗粒和大颗粒存在互相隐蔽和支撑的作用，使得非均匀沙的水下休止角大于粒径与其中值粒径相等的均匀沙的水下休止角。张幸农［4］总结前人成果并结合自己的工作，给出了常用模型沙的物理力学特性，其中塑料沙的水下休止角范围为24°～25°。吕亭豫等［5］采用概率论方法和力学理论分析了水下休止角，给出了不同理论下的表达式，不过并未经过试验验证，其适用性有待观察。目前对于水下休止角的研究仍以试验手段为主，由于试验材料、试验方法等的不同，所得成果多为经验性的，不同成果之间也存在一定的差别。

沉速是模型沙另一重要特性，在研究泥沙颗粒在流体中的运动，特别是涉及泥沙淤积、水流挟沙能力、动床河工模型设计等问题时，都需要知道泥沙颗粒个体或群体的沉速［6］。泥沙单颗粒沉速问题已取得大量理论和经验的成果，实际应用中可选用相应公式进行计算，但在河工模型试验中，模型沙均为混合沙，而对混合沙沉降规律的认识还不够透彻。郑邦民等［7］从流体力学原理出发，推导出了固体颗粒群体沉速的理论解，采用黄河实测资料验证基本符合。费祥俊［8］指出想从非均匀沙中找出平均粒径或中值粒径作为代表粒径来计算群体沉速，往往难以符合实际情况;同时提出可将全部颗粒按粒径粗细分成若干组，计算分级泥沙的沉速，然后按质量加权，求得非均匀沙的群体沉速，这对于动床模型试验选沙而言不失为一种简便有效的方法。

对于以研究底沙冲淤问题为主的河工模型，控制模型沙选择的一个主要条件是起动流速相似［9］。对天然沙的起动流速前人做了大量工作，常用公式有沙莫夫公式、张瑞瑾公式、唐存本公式、窦国仁公式［10］，但由于泥沙起动问题的复杂性和随机性，这些公式均为经验性公式，对新型模型沙的适用性有待进一步验证。王延贵等［1］通过试验得到散粒模型沙的起动流速可以用沙莫夫公式描述，并得出模型沙各起动阶段的沙莫夫系数。不同材料的模型沙物理特性跟天然沙不同，因此不能简单地将天然泥沙的起动理论套用到轻质模型沙中。

本文通过试验对一种复合塑料模型沙的水下休止角、群体沉速及起动流速等运动特性进行研究，并用已有研究成果对试验结果进行对比验证，从而为动床模型试验选沙提供依据。

1 模型沙级配及密度

试验所用模型沙为复合塑料沙，主要成分为不饱和塑脂。用XSZ-200型标准振动筛和HANGPINGJA2003电子秤进行颗分试验。在总体中取出3组样品进行筛分测量，得到其平均的级配曲线如图1所示。通过图1可以查得模型沙的特征粒径:d50=0.28 mm，d75=0.62 mm，d25=0.19 mm，非均匀系数Kf=1.82。模型沙的密度ρs采用容量瓶法进行测量。选取100mL容量瓶3个，试验水温为24℃，参照文献［11］对3组试样进行测量，取其密度的平均值1.18g/cm3为模型沙的密度。干密度和湿密度采用环刀法进行测量，分别为0.604g/cm3和1.008g/cm3。

图1 模型沙级配曲线

图2为天然沙与模型沙放大对比图。

图2 天然沙与模型沙放大对比(粒径0.5～1 mm)

2 水下休止角试验

2.1 试验原理

令模型沙在静水中自然落淤成丘，测出丘体高度和底面直径，即可求出水下休止角。

2.2 试验方法和步骤

试验在长宽高均为30 cm的玻璃水箱内进行，图3为试验装置示意图。在水箱底部中央放置一个直径为112 mm的圆盘，丘体即在此圆盘上形成，因此丘体直径d为固定值(d=112 mm)。

图3 水下休止角试验装置示意图

向水箱内注入清水至刚好淹及圆盘上表面，测出此时箱内水深h1。将足量沙样加水浸湿后放入漏斗内并固定在泡沫浮板(30 cm×30 cm)上。继续向水箱内注入清水至一定高度，将漏斗与浮板组合体缓缓放入水中。在此过程中，水将通过漏斗口(口径6 mm)渗入，应注意控制放入速度，使得漏斗口既无漏沙又不对沙样形成明显冲刷，以免沙样出现分级。调整漏斗方位使其在垂向上与圆盘同轴，同时使漏斗口距圆盘上表面初始高度约为1cm。另外应使水箱内水面略高于漏斗内沙样，使整个沙样处于水下状态，如图3所示。

当漏斗内外水面持平后，沙样开始落淤成丘。在此过程中，需要适时调整漏斗高度，使漏斗口与丘顶之间高差始终维持在1 cm左右，可通过继续加水使泡沫板上浮来实现。另外，沙样落淤后漏斗内水沙体积减小会使漏斗口处出现压差，影响沙样自然下漏，因此须及时向漏斗补水。本次试验中，在沙样以上漏斗侧壁开口，可使补水平稳连续。

当丘体覆盖整个圆盘并充分稳定后，取出漏斗及浮板。在此过程中需将漏斗口封住，避免形成水下射流冲击沙丘。然后用虹吸管排出水箱内多余的水，使水面缓慢下降至将要触及沙丘顶部时停止，测出此时水深h2，则水下休止角可由式(1)求得:

式中:φ为水下休止角;H为丘体高度，H=h2－h1。

2.3 试验结果分析

共进行了3组试验，测得的水下休止角见表1，平均值为28.4°，这超出了张幸农［4］所给出的塑料沙水下休止角24°～25°的范围。这与塑料沙的生产工艺有关，以往塑料沙多接近球形，且多由无黏性憎水材料生产，沙粒表面粗糙度较低，使得相同情况下塑料沙的水下休止角较其他类型模型沙小。试验使用的模型沙沙粒表面存在较多棱角且较粗糙(图2)，比传统塑料沙更接近于天然沙，这增大了沙粒之间的咬合及摩擦，使得沙粒之间的支撑作用有所增强，故其水下休止角有所增大。通过试验可知，该模型沙在动床模型试验中可以具备较好的水下成形特性。

表1 水下休止角试验结果(水温24℃)

3 沉速试验

3.1 试验原理

根据费祥俊［8］加权平均的思路进行试验。将沙样按照筛分粒径划分为若干组，对每一组进行若干单颗粒沉速试验并对结果统计平均得出每一组的平均沉速，然后按照分组质量分数加权，求出整体沙样的群体沉速。

3.2 试验方法和步骤

试验在圆柱形玻璃沉降筒内进行，其内径为4 cm，高为100 cm，注入清水垂直放置。为保证沙粒充分发展为匀速下沉并避免沉降筒底部收缩段的影响，在沉降筒距上下两端20 cm处分别标出计时起始线和终止线，两线之间60 cm为有效试验段。试验装置见图4。

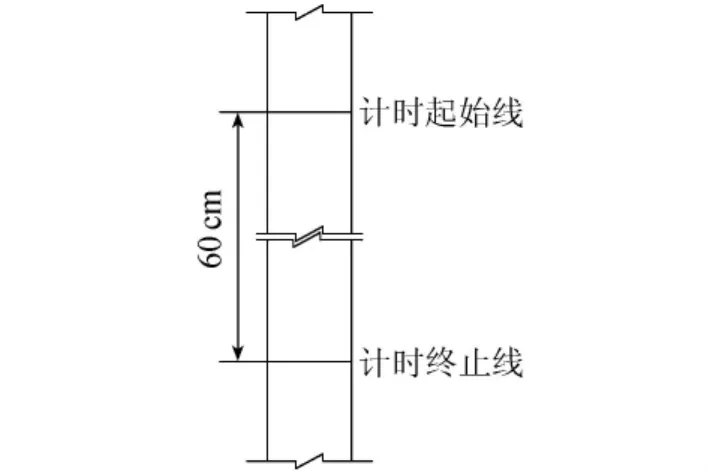
图4 沉速试验装置示意图

式中:ω为沙样群体沉速;ωi为各粒径组平均沉速;n为沙样粒径组数;pi为各粒径组所占质量百分比。

3.3 试验结果分析

试验结果列于表2，计算得ω=1.210 cm/s。由于小于0.125 mm的3个粒径组沉速很小，不便试验，考虑到其所占质量分数较小(12.26%)，且粒径范围不大，其沉速采用武水公式进行计算，粒径值取各粒径组的中值粒径。

测得各试验数据后，用武水公式、W.W.Rubey公式和刚恰洛夫公式3个经验公式［6］对沉速试验结

试验时，每个粒径组取出20颗沙粒，在清水中浸泡1 d进行除气后，分别以单颗粒做沉降试验，记录其经过试验段所用时间，计算出每颗沙粒的沉速，对20颗沙粒沉速求平均得到该粒径组的平均沉速。整体沙样的群体沉速按式(2)求得。果进行验证，见表3。首先把各粒径组中值粒径代入3个公式，将计算所得数据绘制成相应的沉降曲线，见图5;然后将各粒径组的中值粒径与平均沉速对应，点绘于图中与经验公式进行比较。由图5可以看出，实测值与3条沉降曲线吻合较好，说明用上述试验方法测量各粒径组的平均沉速是可靠的。另外，3条曲线比对，实测值对W.W.Rubey公式曲线的收敛效果最佳，因此对于该模型沙，其单颗粒沉速推荐使用W.W.Rubey公式进行计算。

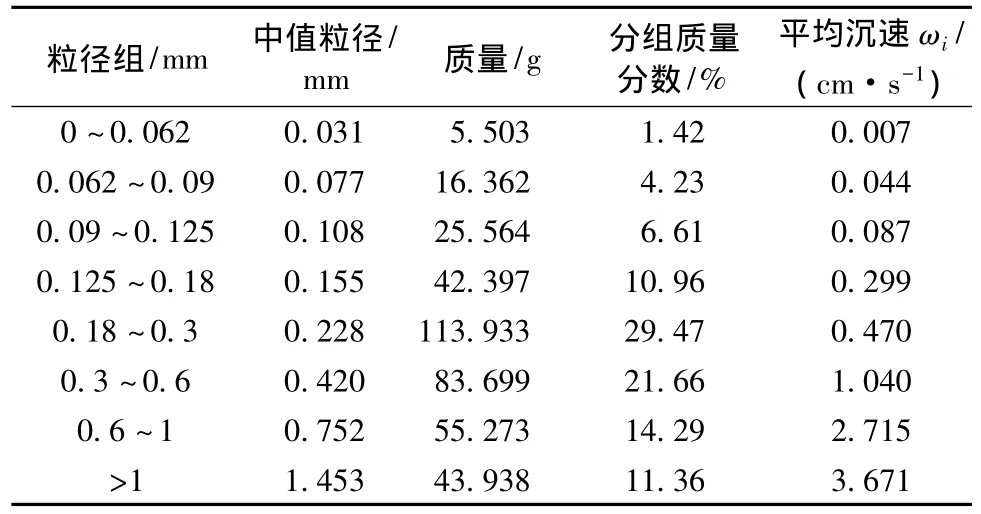
表2 沉速试验结果(水温24℃)

表3 模型沙中值粒径沉速验证

图5 各粒径组实测沉速与经验公式的对比

再用3个公式分别对沙样中值粒径0.28 mm进行沉速计算，同时求出试验群体沉速1.210 cm/s对应各公式的粒径，列于表3。可以看出，将中值粒径代入经验公式求出的沉速值均较测量值偏小，这种不一致性从群体沉速值对应的粒径情况也可看出。由此可见，在动床模型试验中，对于模型沙的群体沉速，用中值粒径进行经验计算的结果往往不能保证足够的精度，应该通过试验来测定。

当然试验的方法也有其局限性。在本次试验中，试验沙粒个数、试样粒径组合、读数的主观性等都会影响试验的精度。由于各组的平均沉速难以随颗粒个数的增加呈现出较明显的收敛特征，因此尽量减小各粒径组的粒径范围并增加试样沙粒个数是提高试验精度的有效措施。

4 起动流速试验

4.1 试验设备及方法

试验在长6m、宽0.2m、高0.3m透明玻璃边壁的可变坡循环水槽中进行。上游进口处放置蜂窝状水流矫直机来平顺水流。上游1.5 m及下游1.0 m为平顺水流段，中段3.5 m铺沙，观测段设在铺沙段中部。起动流速用LGY－II型光电式旋桨流速仪测得，测点设于距河床0.4h(h为水深)处。

试验前将沙样加水充分浸润1 d，铺沙厚度为4 cm，保持适度密实、床面平整，铺沙的两端分别放置坡度较缓的平水楔以稳定流态。试验开始时，在上游段放置挡板，升起尾门至一定高度，由下游放水逐渐淹没河床后浸泡铺沙段30 min，以清除床面下气泡。由于气泡排出床面使床面平整受损，需再次抹平床面，然后再从下游放水至淹没河床，完全淹没后继续放水至所需水深。打开水槽的流量控制阀由上游放水，至挡板两侧水深相同时，除去挡板，此时可通过调整流量、尾门及水槽坡度得到需要的均匀流条件进行试验。分别进行了水深为5 cm，7 cm，10 cm，15 cm，20 cm这5种工况下的起动流速试验。测量流速时，必须保持控制段为均匀流并已维持一定时间，本次试验中每种工况稳定后保持10 min以观测床面变化并记录流速等资料。

在正式试验前需进行预备试验，以初步校准流量、尾门和坡度，并得到起动流速的大致范围。

4.2 试验结果分析

不同水深下，各起动状态对应流速见表4。

表4 各水深起动流速实测值

试验所得3个阶段的起动流速均比张幸农［4］总结的塑料沙的起动流速大，这与水下休止角的试验结果是相符合的。一方面因为试验采用的是复合塑料沙，其密度不如传统单一材料模型沙稳定，且平均密度1.18 g/cm3较传统的塑料沙1.05 g/cm3大;另一方面沙粒表面有较多棱角且较粗糙(图2)，比传统塑料沙更接近于天然沙，增大了沙粒间的咬合与摩擦力。

将实测的起动流速与几个经验公式得到的起动流速曲线同绘于图6。可以看出，3种起动状态起动流速随水深的变化规律与沙莫夫和唐存本公式符合较好，而与水深有关的公式中沙莫夫公式应用较多，因此考虑通过调整沙莫夫公式中的系数对3种起动状态的实测值进行拟合。

图6 模型沙起动流速实测值与经验公式的对比

将沙莫夫公式中的常数1.14改为系数K，泥沙粒径采用中值粒径d50可得:

式中:uc为起动流速;H为水深;ρ，ρs分别为水和泥沙的密度;g为重力加速度。

用本试验数据拟合式(3)得3种起动状态下K值分别为 1.36，1.64，1.89。与王延贵等［2］得出的1.09，1.34，1.94 和府仁寿等［12］得出的 1.71，2.08，2.70相比，本文的K值介于两者之间。拟合结果如图7所示。个别起动与少量起动时，实测数据与拟合公式的计算数据吻合较好，表明沙莫夫公式能够较好地描述此模型沙个别起动与少量起动的流速。而大量起动时吻合精度相对较低，这是因为:①宽深比较小，流速增大到大量起动阶段时，边壁将对水流结构产生较大影响;②观测段铺沙级配对起动流速有直接影响，因此铺沙时应尽量使床面均匀;③旋桨式光电测速仪是接触式的测速仪，其本身对水流存在一定的影响。

图7 模型沙起动流速实测值与沙莫夫公式拟合曲线对比

5 结论

a.试验测得该塑料沙水下休止角为28.4°，比通常认为的塑料沙水下休止角范围24°～25°大。在动床模型试验中，该模型沙可以具备较好的水下成形特性。

b.试验测得模型沙的群体沉速为1.210 cm/s，该沉速对应的武水公式、刚恰洛夫公式和W.W.Rubey公式中的粒径分别为0.441 mm，0.515 mm和0.405mm，均较该模型沙中值粒径0.28mm大很多，因此群体沉速应通过试验确定。通过代表粒径方便地计算群体沉速具有重要的工程应用价值，这里的代表粒径可以突破常用概念的限制，选择中值粒径、平均粒径等以外的代表粒径，这有待深入研究。

c.试验测得模型沙起动流速大于传统塑料沙，这与水下休止角的试验结果是符合的。

d.起动流速随水深的变化规律与沙莫夫公式及唐存本公式符合较好。个别起动与少量起动时，实测数据与拟合公式的计算数据吻合较好，大量起动时吻合精度相对较低。

［1］王延贵，王兆印，曾庆华，等.模型沙物理特性的实验研究及相似分析［J］.泥沙研究，1992(3):74-84.

［2］张红武，汪家寅.沙石及模型沙水下休止角试验研究［J］.泥沙研究，1989(3):90-96.

［3］金腊华，石秀清.试论模型沙的水下休止角［J］.泥沙研究，1990(3):87-93.

［4］张幸农.常用模型沙及其特性综述［J］.水利水运科学研究，1994(1/2):45-51.

［5］吕亭豫，陈贤策.泥沙颗粒水下休止角的研究［J］.价值工程，2012(20):67-68.

［6］王兴奎，邵学军，李丹勋.河流动力学基础［M］.北京:中国水利水电出版社，2002:54-59.

［7］郑邦民，夏军强.固体颗粒的群体沉降速度分析［J］.泥沙研究，2004(6):40-45.

［8］费祥俊.泥沙的群体沉降:两种典型情况下非均匀沙沉速计算［J］.泥沙研究，1992(3):11-20.

［9］左东启.模型试验的理论和方法［M］.北京:水利电力出版社，1984:114-115.

［10］钱宁，万兆惠.泥沙运动力学［M］.北京:科学出版社，2003:240-271.

［11］陈俊杰，任艳粉，郭慧敏，等.常用模型沙基本特性研究［M］.郑州:黄河水利出版社，2009:21-23.

［12］府仁寿，卢永清，陈稚聪.轻质沙的起动流速［J］.泥沙研究，1993(1):84-91.

Experiment of motion characteristics of a kind of plastic model sediment

TANG Limo1，2，LIU Quanshuai2，HAN Keyao2，XIAO Yang1，2(1.State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering，Hohai University，Nanjing210098，China;2.College of Water Conservancy and Hydropower Engineering，Hohai University，Nanjing210098，China)

An experimental study was performed on the submarine repose angle，group settling velocity，and incipient velocity of a kind of compound plastic model sediment.The submarine repose angle can be determined from the geometric relationship of the cone formed by the model sediment accumulating naturally in static water.The sediment sample was divided into different groups according to diameter to perform the single particle settling experiment.Then，the arithmetic average settling velocity of each group was calculated and the group settling velocity was obtained with the weighted average of all groups.The incipient velocities under five kinds of water depth were measured in a glass flume and were verified by experienced formulas.Experimental results show that the submarine repose angle was 28.4°，larger than the value of traditional plastic sediment，which manifests outstanding underwater shaping ability;the W.W.Rubbey formula is acceptable for calculating single particle settling velocity，but it is not accurate enough to calculate the group settling velocity using formulas with the median particle diameter，meaning that the proper representative diameter needs further research;the incipient velocities measured are larger than the traditionally used ones，corresponding to the submarine repose angle experiment;and Shamov’s formula can properly formulate the states of individual initiation and a small amount initiation by adjusting the coefficientK，while it is not accurate enough for the state of a large amount of initiation.

plastic model sediment;submarine repose angle;group settling velocity;incipient velocity

TV149

A

1006-7647(2012)06-0070-05

10.3880/j.issn.1006-7647.2012.06.018

国家自然科学基金青年科学基金(50909036);河海大学水文水资源及水利工程科学国家重点实验室基本科研业务费自主研究项目(2011585712，2010585512);水利部公益性行业科研专项(200901005)

唐立模(1977—)，男，山东烟台人，副教授，博士，主要从事泥沙运动力学与河流动力学研究。E-mail:tanglimo@hhu.edu.cn

2012-08-21 编辑:熊水斌)