卧式储液罐储液量计算方法设计与研究

齐宝军，石 强，马 瑾

（中国石油长庆油田公司第三采气厂，内蒙古乌审旗 017300）

1 卧式罐储液计算以往状况

苏里格气田在天然气生产的过程中，会产生凝析油与水的混合液，气田生产中，集气站、处理厂接收和处理这些液体的罐，多为 20 m3、30 m3、50 m3的卧式储罐（见图1）。

但是鉴于储罐两端部分为椭球体形式，其中液体的升降中为不规则形体，经典计算中没有成型的计算公式，利用积分计算也不方便，这给准确计算带来一定的困难。

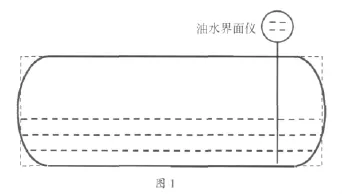
气田以往的计算中，基本忽略了球冠部分的影响，把罐体直接当成圆筒体进行储液量处理（如图1的虚线部分）—利用积分法计算出不同高度储液体积的数据表，然后根据数据表对照结果，计算出罐内不同高度范围罐中的储水量和储油量，这样计算本身存在数学上的人为误差。加之液位计精度偏差等问题，工作人员不能很好的掌握罐内不同高度间准确的液量。

2 计算卧式储罐内液量的方法

经过研究角函数关系式等，利用常规方法，确定下面的相关公式。

2.1 计算圆筒部分液体

（1）当液体高度小于罐体半径时，其横截面（见图2）。

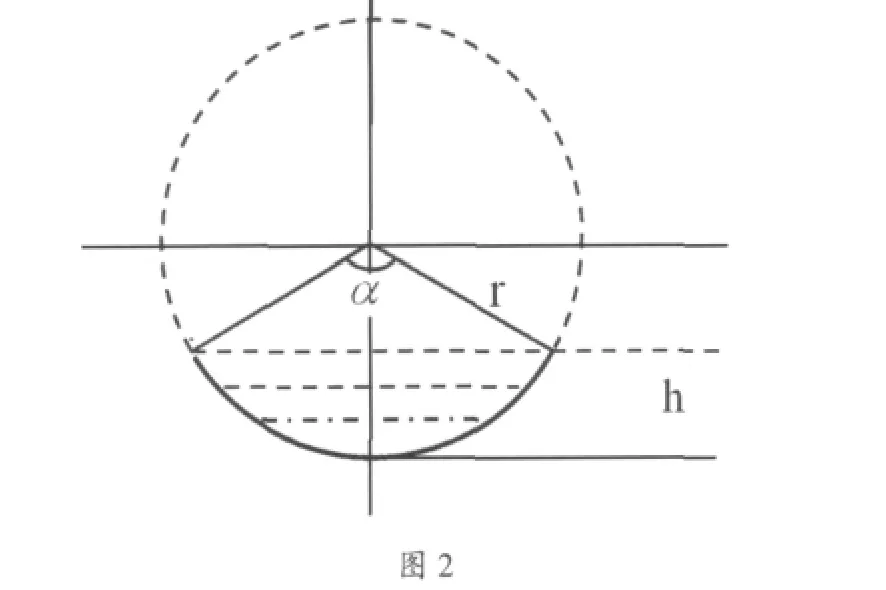
其中：α为液面两端与圆心的夹角；r为圆筒半径；h为液面高度。

利用反正切关系，得到下面的公式

利用扇形计算公式，可得到液体的横截面积为：

（2）当液体高度大于罐体半径时（见图3）。

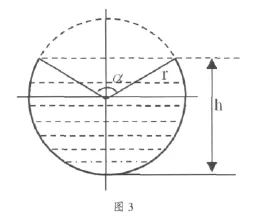
利用反正切关系可求出图3的夹角α：

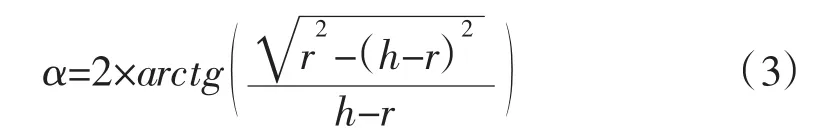
再利用扇形计算公式，得到水体横截面积为：

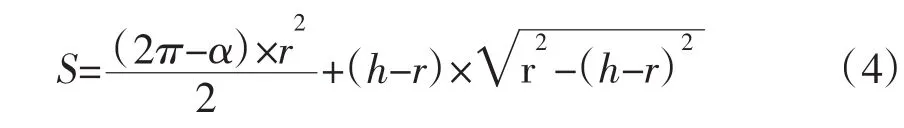
设圆柱部分长度为L，则圆柱部分的液体的体积（见图4），由公式2或公式4可得：

2.2 计算椭球球冠部分液体体积

因为罐体两端是对称的半椭球球冠，运算中可以合成一个完整的球冠进行计算（见图5）。

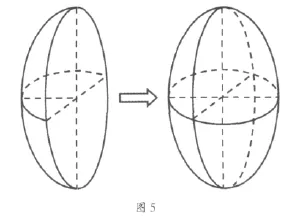
罐体横截面为圆形，所以此球冠的长轴=中轴，短轴一般为罐体半径的一半左右(依实际为准)，则球冠的正视图为椭圆形（见图6），侧试图为正圆形（见图7）。而球冠内的液面俯视图为椭圆形（见图8）。

对照图6、图7、图8，只要求出规定高度上椭圆形水平面的长轴短轴a'、b'，则对应高度的椭球内水平截面的面积可求，这样就为求出椭球内液体积了提供可能。

根据椭球正视图图6，由椭圆性质公式（6），r为正视图椭圆的长轴a，而该椭球的短轴b即是其自身短轴，以垂直方向为x轴，即可得出公式（6）的y值，即俯视图（见图8）椭圆水面的短轴b'。

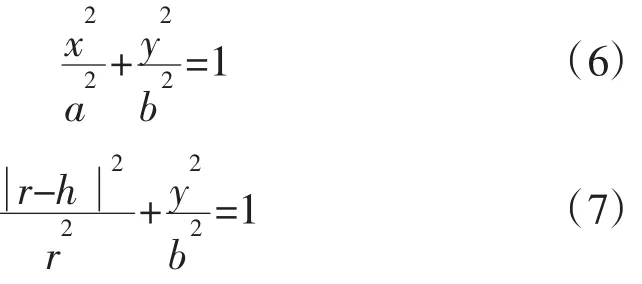
由公式（7）可得：

而a'的算法，则根据测视图（见图7），利用数学三角关系可得：

再根据椭圆面积公式，即可得出指定高度h处—水平面椭圆的面积为：

这样，即可算出球冠内任何高度的液体面积，也就为进一步计算不同高度液体体积做好了准备。

3 电脑程序的设计

根据以上推导的计算方法，在电脑上，笔者首先建立了两个主要的面积计算函数，即

圆筒部分—根据液位高度计算液体横截面面积的函数。

计算主程序：

（1）对圆筒部分的液体的体积，直接用底面积乘以高的办法，一次性求出。

（2）对椭球冠部分液体的体积，根据对计算结果精度的需要，以毫米为递加单位，利用循环累加的方式，不断计算出各个层位椭圆液面的面积—也即每个毫米层的微体积，并累加这些微体积实现积分，直至累加至指定高度，这样即实现了计算指定高度球冠内液体体积的目的（见图9）。

设计2个程序的界面（见图10、图11）。

4 应用效果

应用该方法编制出的计算程序，与经典计算公式计算整体体积的结果相对照。经典对照公式如下：

圆筒部分体积：

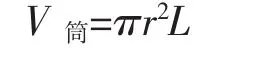
椭球部分体积：

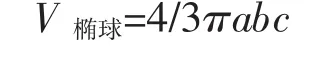
罐的总体积为：

表1、表2分别是根据罐的设计数据，利用公式（11），以立方米为单位，取保留三位小数作为计算的结果。而图10、图11，分别是以表1和表2数据为依据，程序以积分方法计算的结果。

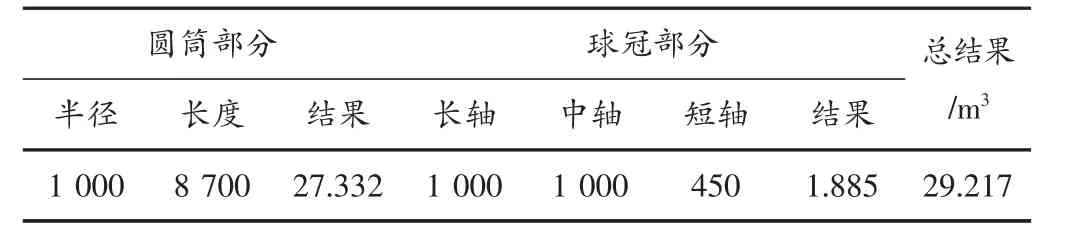
表1 某罐设计数据及计算结果

表2 某罐设计数据及计算结果

其中，可以看出：

图10程序所计算的总体积与表1结果完全吻合，图11程序所计算的总体积与表2结果完全吻合。

5 拓展与展望

此方法中没有提及罐体为椭圆形储罐的计算，但实际通过以上相关的公式，完全可以推导出该类罐不同液位下的体积。

该方法以高中知识即可理解，只要掌握编程技术，既可以编写出电脑程序，计算出所需精度的液量结果。

参考书籍：

［1］彭良译，何炳全，等.高等数学［M］.四川：西南石油大学 ，1994.

［2］郑启华.PASCAL程序设计［M］.北京：清华大学出版社 ，1994.

［3］徐万力.DELPHI5实力精通［M］.北京：清华大学出版社 ，2000.