基于最小二乘支持向量机的开都河径流预测

王 暄，屈卫军

(新疆巴州水利水电勘测设计院，新疆 库尔勒 841000)

基于最小二乘支持向量机的开都河径流预测

王 暄，屈卫军

(新疆巴州水利水电勘测设计院，新疆 库尔勒 841000)

简述支持向量的回归分析，支持向量机自回归预测模型结构及预测方法，利用开都河大山口水文站52 a的径流资料，采用最小二乘支持向量机方法对径流进行模拟预测，并与BP神经网络方法进行对比分析，其计算结果相对略好。

支持向量机;径流预测;BP神经网络;开都河

河川径流的中长期预报是水资源合理利用和优化调度决策支持系统工作中的重要环节，在防汛、抗旱、发挥水利设施的经济效益及流域水利规划等方面都具有十分重要的作用。中长期径流预报方法可分为传统方法和新方法两大类，前者主要有成因分析和水文统计方法，后者主要包括模糊分析、人工神经网络、灰色系统分析等方法。受天文因子、气候因子、植被因子、地质地貌因素和人类活动的综合作用，水文系统表现出高维性、非线性、随机性、模糊性、混沌性等复杂特征，所以定量的机理分析是有限而困难的［1］。目前一种新的机器学习方法即支持向量机 (Support Vector Machine，简称SVM)越来越多的运用在回归问题研究上，支持向量机通过某种函数可以实现到高维空间的非线性映射，适合解决非线性的回归问题。径流预测问题具有显著的非线性特性，因此SVM方法很适合应用于解决该问题。

1 支持向量机研究方法

SVM是在统计学习理论基础上发展起来的一种新的机器学习方法。机器学习研究从观测数据出发寻找规律，利用这些规律对未来数据或无法观测数据进行预测，其重要理论基础之一是统计学。支持向量机又称支持向量网络，具有理论完备、适应性强、全局优化、训练时间短、泛化性能好等优点。最小二乘支持向量机(LS－SVM)是支持向量机的一种，它是将标准支持向量机算法中不等式约束转化为等式约束而得到的［2－4］。

1.1 支持向量回归分析

支持向量回归是支持向量机用于回归中的情况。SVM方法是从线性可分情况下的最优分类面发展而来的。对于回归模型，设给定的训练样本为:

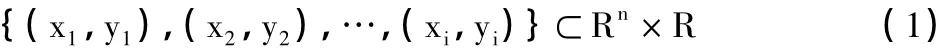
采用一个非线性映射φ把数据映射到一个高维特征空间，然后在高维特征空间进行线性回归，设回归函数为:

高维空间优化中的内积运算采用满足 Mercer条件［5］的核函数 k(x，y)代替，使得 k(x，y)=［φ(x)，φ(y)］，常见的满足Mercer条件的核函数有:

(1)多项式核函数:

(2)高斯径向基函数:

(3)Sigmoid函数:

利用最小二乘支持向量机，求得非线性回归函数的表达式为:

式中:a为拉格朗日乘子;b为偏置值。

1.2 支持向量机自回归预测模型

序列预测问题可以看成一个函数回归的问题，回归分析就是假定已知数据间存在某种不确定性的关系，而这种关系可以通过分析构造某一函数来表达，然后通过这一函数关系来进行预测分析。

对于自回归模型，可以假设训练样本数为 n，根据嵌入维数 m，输入向量 Xi=［xi，xi+1，…，xi+m－1］，i=1，2，…，n － (m－1)和输出 Yi=xi+m，i=1，2，…，n－ (m －1)，建立模型:

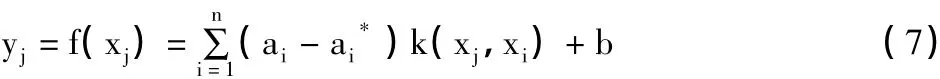
预测阶段输入xn+1，根据上述模型得:

2 基于LS－SVM模型的开都河径流预报

径流预报是开都河大山口水库进行优化调度的基础，若预报的信息可靠，调度适当，能比没有预报调度取得明显的经济效益。

2.1 模型建立

1)数据预处理。为加速收敛速度，通常需对输入数据进行预处理。一般采用的预处理方法是将输入数据0－1归一化，即将输入的数据进行变换，使之位于(0，1)区间内，常采用的变换有线性函数和Sigmoid函数。本文采用线性化函数对输入数据进行预处理，具体函数表达如下:

式中:xmin为输入数据中的最小值;xmax为输入数据中的最大值;n表示训练样本的总个数。

2)选择满足Mercer条件的核函数 K(xi，xj)。对于一个特定的核函数，给定的样本中的任意一个样本都有可能成为一个支持向量机，但在此支持向量下观察到的特征在其他核函数下并不保持，也就是说不同的核函数可能对应不同的支持向量，所以核函数的选择很重要。径向机函数(Radial Basis Fuction，简称RBF)核函数，只有一个参数 σ，又由于核参数能够反映模型选择的复杂度，同时RBF核函数是一个普适函数，通过参数的选择，它可以适用于任意分布的样本，综上所述，本文选择径向基函数:

作为核函数。

3)采用K.Pelckmans等人开发的LS－SVMlab1.5的应用软件作为核心软件，在 MATLAB6.1中编程实现。

2.2 实例应用

根据开都河大山口水文站1956～2007年52 a径流资料，进行预测分析。根据3年小周期现象［6］，以 1956～2004年的时间序列每3 a一个训练样本，对应下3年的径流量为输出值。即以1956～2004年的数据为训练样本，将2005～2007年的年径流量作为预测模型的检验。本文训练样本n=49，预测样本 m=3。采用上述最小二乘支持向量机方法进行径流预测计算，其模型检验结果见表1所示。

表1 径流量预测结果(LS－SVM方法)

为说明问题，在相同情况下，也采用BP神经网络方法进行对比研究。同样利用MATLAB6.1来实现计算过程。通过反复的试错和训练，得到如下BP模型结构:输入节点数为3，隐含层节点数为5，输出节点数为3，隐含层采用双曲正切 S型(Tan－Sigmoid)传输函数，线性(Purelin)传输函数作为输出函数，Levenberg－Marguardt函数作为训练函数，计算结果见表2。

表2 径流量预测结果(BP方法)

通过以上计算结果表明，无论采用最小二乘支持向量机方法还是神经网络方法都可以进行径流预报，但就两种方法计算结果的相对误差结果分析，利用最小二成支向量机方法比神经网络方法的结果要略好。

3 结语

尽管仅以三年的预测值并不能完全表明在进行长期径流预测时支持向量机方法优于神经网络方法，但在计算过程中，最小二乘支持向量机方法的优越性得到充分体现:径向机核函数，只有一个参数σ，在试算调整过程中只要该方法的结构确定了，计算结果也就确定了，而神经网络方法由于存在局部极小的现象，因此模拟结果并不唯一。

综上可以得出，采用最小二乘支持向量机方法进行径流长期预报在理论上是可行的，相对而言该方法比神经网络方法计算效率高，而且克服了神经网络易陷于局部极小值的缺点，下一步将对提高预测精度问题进行深入研究。

［1］王文圣，丁晶，李跃清著，水文小波分析［M］.北京:化学工业出版社.2005:142.

［2］宇缨，李清华.统计学习理论和支持向量机［J］.沈阳大学学报.2005，17(4):42 －47.

［3］佟春生.系统工程的理论与方法概论［M］.北京:国防工业出版社.2005:165－172.

［4］林剑艺，程春田.支持向量机在中长期径流预报中的应用［J］.水利学报.2006，37(6):682 －686.

［5］边肇棋，张学工.模式识别(第二版).北京:清华大学出版社.2000.

［6］徐国昌，董安详.我国西部降水量的准 2a周期［J］.高原气象.1982，1(2):11 －16.

Forecasting of Kaidu River Runoff Based on LS－SVM Model

WANG Xuan，QU Wei－ Jun
(Bazhou Exploration Design Institute of Hydro－power and Water Resources，Kurle 841000，China)

The paper introduced the support vector regression analysis，expounded on support vector machine auto－regression model structure and prediction methods.The runoff data of 52 years were taken for runoff prediction by using least square and Support Vector Machine method(LS－SVM). A contrast analysis was made with the BP neural network method，which showed that the computed result was relatively better than the BP neural network method.

SVM，runoff forecasting，BP neural network and Kaidu River

P338+.9

A

1004－1184(2012)05－0090－02

2012－05－16

王暄(1976－)女，新疆库尔勒人，工程师，主要从事水利工程规划设计工作。