傍河抽水驱动下河流与地下水关系演化的数值模拟研究发展概况及存在的问题

姚珂君，王文科，王世东

(1.中煤科工集团西安研究院，陕西 西安 710054;2.长安大学环境科学与工程学院，陕西 西安 710054)

傍河抽水驱动下河流与地下水关系演化的数值模拟研究发展概况及存在的问题

姚珂君1，王文科2，王世东1

(1.中煤科工集团西安研究院，陕西 西安 710054;2.长安大学环境科学与工程学院，陕西 西安 710054)

研究河流与地下水关系的演化过程，对深化沿河地段地下水资源形成的认识，发展与创新河床下地下水运动的理论和研究方法具有十分重要的理论和实际意义。通过对已有的国内外关于傍河抽水模型的研究成果进行收集分析，总结出傍河抽水驱动下河流与地下水关系演化的解析解模型和数值解模型的研究进展，以及在已有模型研究中对模型概化存在的不足。并指出随着地下水的超采，地下水位持续下降，河流和地下水之间失去直接水力联系，地下水流以非饱和渗流为主。以及对该问题的研究方向的展望。

数值模拟;傍河取水;河流与地下水;关系演化;研究进展

傍河水源地主要依靠袭夺河水资源量得以补给，一般具有很强的储存和调蓄能力，以其水量稳定、净化水质、增大区域水资源利用率的优点著称。但是如果开采不合理，就会直接导致地下水位持续下降、地下水污染，地面沉降，地裂缝等严重的生态环境问题，同时地下水开采也会引起河流的水量减少、河道淤积、河水自净能力减弱、地表生态环境的恶化及气候条件的改变等。因此，建立准确可靠的河流地下水模型，对傍河水源地的开发和管理具有重要的作用。

1 解析解模型研究的发展概况及存在的问题

在早期的研究中，Theis［1］(1935)首先提出的河水地下水转化模型，即泰斯井流模型(图1)。它是在假定含水层承压、均质各向同性、厚度相同、底板水平、在平面上无限展布等条件下的无越流补给的完整单井的水流模型。该模型通过数学变换和数学推导后，得泰斯井函数。该函数被认为是从稳定井流发展到非稳定井流的一个重要标志。但是该模型的适用条件十分苛刻，在实际应用中受到了很大限制。1941年在泰斯井流的模型基础上，他又提出了完整河渠傍完整井抽水模型(图2)，该模型不考虑弱透层的影响，可用于模拟承压含水层抽水，也可以近似模拟符合Dupuit假设的潜水含水层抽水［2］。

M.S.Hantush 和 C.E.Jacob［3］(1955)在泰斯井流模型的基础上提出了考虑越流补给的井流模型(图3)，推导出汉土什公式。该模型应用于第一越流系统中的井流，不考虑弱透水层的弹性释水，只考虑隔水层的越流渗流。在这种假设下，弱透层中的渗流已被看成是铅直方向的一维水流，主含水层中的水流呈水平方向，这就使得问题简化，计算方便。但是如果从严格的理论上推敲，就可以发现这些假设的一些矛盾之处，例如，在实际水流问题中，由于弱透层透水，弱透层与主含水层分界面处水流的法向分速度就不为零，而且由于含水层中的水流是流向抽水井的，所以该分界面既不是流面也不是等水头面，而该模型却假设水流方向在该分界面做90度转折，即该分界面既是流面又是等水头面。

图1 Theis井流示意图

图2 Theis傍河抽水模型

Hantush［4］(1965)提出了潜水含水层，完整河渠傍抽水影响下，河水地下水转化的解析解模型(图4)，该模型是在泰斯模型的基础上考虑了河床周围弱透层对地下水转化的影响，弱透层单层垂向分布，将河流和含水层隔开。

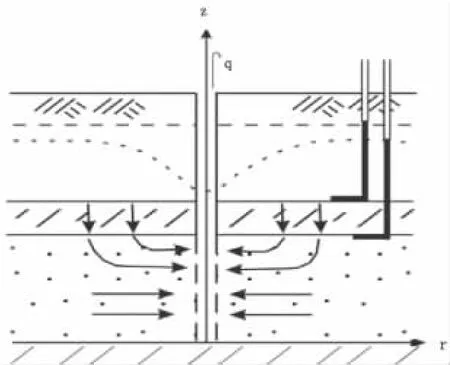
图3 Hantush井流模型

Hunt［5］(1999)进一步研究了傍河抽水模型(图 5)，模型要求假设含水层无限展布，河床周围有弱透层的非完整河渠位于完整井抽水的有效影响半径范围内，弱透层在河床周围是单层均质等厚的，含水层是均质各向同性的，并且抽水过程中地下水潜水面的下降幅度较小。相对于前者，该模型模拟了更复杂的河流地下水转化问题，与MODFLOW软件模拟的结果拟合的更好。但是从假设条件可以看出，该模型对于大强度抽水后，河流与含水层失去水力联系的情况是不适用的，并且也没有考虑越河渗流的问题，以及河渠宽度对模型的影响。

图4 Hantush傍河抽水模型

Garey A.Fox 和 Paul Duchateau［6］等(2002)在上述 Hunt的基础上建立了考虑河渠宽度的傍河抽水解析解模型。模型求解后得出，当河中心距抽水井的距离L是河宽W的25倍以上时(图6)，河流宽度的变化对模型结果是没有影响的，可以忽略;但是如果该比例不到25，在模型计算时，就应该考虑河流宽度对计算的影响。

图5 Hunt傍河抽水模型

图6 河宽因素示意图

可以看出，以解析解模型来研究傍河抽水影响下河流与地下水转化，能实现以函数的形式准确直观的反映河流与地下水转化的关系，但其只适用于理想状态或结构简单的含水层。并且在求解过程中为了模型条件的的简化，它们一般都忽略了以下四点:

(1)河流切割含水层的完整程度;

(2)河床弱透层的复杂结构;

(3)抽水后含水层的弹性释水;

(4)大强度抽水后，河水和地下水失去水力联系，河流向地下水的补给转化为非饱和渗流。

模型的简化导致河流和地下水转化量计算不准确，也使得含水层中的水头分布失真。

2 数值解模型研究的发展概况及存在的问题

鉴于采用解析解数学模型研究傍河抽水影响下河流与地下水转化问题存在的不足，以及对于实际复杂的水文地质条件下的河流与地下水转化的认识，很多专家学者模型采用数值模拟的方法进行研究。

Jurgen Shubert［8］(2002) 在德国的 Rhine 河附近进行了长期的动态观测和抽水试验，建立数学模型，以研究该河流和地下水的转化关系。该河流周围地质结构复杂，河床弱透层大致可以分为两层，上层为物理淤积，下层是化学淤积。通过建立有限元模型求解，将研究区的含水层分为7层进行有限元三维网格剖分(包括4000多个节点)，抽水井区域被剖分为10层。通过多年的动态观测资料及模型求解后发现，河床的渗透系数是随时间季节及来水量的冲刷是发生变化的，而且从河流到抽水井位置，含水层的渗透性能是成层逐步变化的，是非均质的。

Xunhong Chen 和 Longcang Shu［9］(2002)用 MODFLOW 中的River package模拟了傍河抽水影响下河水和地下水的转化。他们得出，在抽水开始后不久后河流的基流量就开始减少，并且在抽水停止很长一段时间内，基流量还在减少，大约占河水流量减少的90%以上，而河床渗漏对河水流量减少的影响不到10%。总的来说在抽水停止后，对于河床弱透层比较厚的，渗透性比较差的河流，基流量减少对河流量减少起到更大的作用，所以抽水驱动下河流量的减少量和河床的渗透性也不是呈线性变的。

由于对水资源的利用方式以抽水井为主，所以国际上对傍河抽水井影响下地下水运动的研究起步较早，研究程度较高，理论也发展的较为成熟。相比之下，对于河渠影响下的地下水运动的研究就比较少，而且是以洪水作用下河流对地下水的影响最为常见。

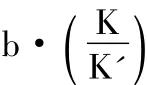
Mohamed M.Hantush［11］(2005)研究了河床周围有弱透层存在的非完整河渠，在洪水作用后河水和地下水相互转化的解析解(closed－form solutions)。该模型假设含水层不是无限展布的，只存在于有限区域内，均质各向同性。在洪水发生时，河流补给地下水，地下水位升高，含水层中储水量的增大(图7A);洪峰过后，地下水补给河水(图7B)，河流基流量增大。可以看出该过程对河流的洪峰过程起到一个减缓的作用，但是文中对该过程的研究忽略了河床下地下水流的垂向二维流动，采用了线性化的布西尼斯克方程，所以由文中模型计算得出的河流和地下水的转化量也是不够准确的。

图7 洪水作用下河流与地下水转化示意图

对于河流和地下水之间存在的非饱和渗流，很早就有人提出来，但是真正有实质性研究却是从近40年才开始的。

Riesenaur［12］(1963)首次提出了无水力联系状态下河流和地下水转化的数学模型，并通过变饱和有限差分求解含水层中的含水率分布和压力水头值。模型结果得出:在河水入渗时，河流和地下水之间存在非饱和区，并且一直到稳定状态时这个非饱和区域依然存在。由于河流和地下水失去水力联系后，潜水面和河床距离较远，所以在这种情况下只能是河流补给地下水。

Peterson 和 Wilson［13］(1988)通过建立非稳定流数值模型，研究在傍河抽水驱动河流补给量增加情况下，非饱和区河流地下水转化的影响因素。研究结果表明，当河床周围存在明显的弱透层时，河流和地下水之间就容易产生非饱和渗流区。Peterson和Wilson还在文章中指出，尽管河流和地下水之间存在非饱和渗流区，但是它们之间还是存在某种意义上的水力联系，当排泄水位降低时，河流的渗漏量也会随之增加。这与现在普遍认识是不符的。

Stephen［14］(1996)通过实验研究观测到，随着地下水位降低，河流和地下水就会失去水力联系，河流以非饱和渗流形式补给地下水，在河流和地下水之间产生非饱和渗流区。在到达这一状态后，这种脱节状态就成为稳定状态，不再随时间发生改变。并且当地下水位继续下降时，河流的渗漏量不再发生改变。该研究还发现，在河床底部存在一个厚度不大的悬挂饱水带，而不是之前人们普遍认为的河床饱和渗流区直接过渡到非饱和渗流区。

Bouwer和 Daddock［15］(1997) 对河流和地下水的转化关系研究后指出，对于河床存在弱透层时，随着地下水位的下降，河流和地下水之间出现非饱和渗流区，此时河流和地下水之间就失去直接水力联系，河流的渗漏量只与河水位、河床弱透层渗透性有关，不再随地下水位的变化而改变。

Fox和 Durnford［16］(2003)研究了垂向一维状态河流与地下水脱节演化过程，文中把随着地下水位的下降，河流从饱和渗漏补给地下水到非饱和渗流补给的演化过程归纳为三个阶段:

(1)饱和水流，当地下潜水面的位置在河床底板以上，河水饱和渗流补给地下水;或者是地下水潜水面略低于河床底板，河床底板处于负压状态，但此时该负压值小于进气值时，该水流处于饱和水流。此时河流渗漏量直接受潜水面的位置影响，渗漏量可表示为:

潜水面位于河床底板以上:

潜水面位于河床底板处:

潜水面略低于河床底板:

其中Sw指河流水头与潜水面的水头差;Hw指河水深;M是河床弱透层厚度;hw是河床底部压力水头，当潜水面低于河床底板时为负值;ks是河床饱和渗透系数。

(2)过渡水流，是从饱和到非饱和水流的一个中间过渡状态。潜水面低于河床底板，河床仍处于饱和状态，但是河床下存在非饱和区，区内负压水力坡度较小，略小于单位1(图8)。此时河流渗漏量主要受非饱和渗透系数影响:

其中hc是毛细压力水头，k(hc)是非饱和渗透系数，是一个随着负压值增大而减小的函数，一般用 Brooks－Corey或Van Genuchten等模型描述。

图8 过渡渗流状态

图9 完全非饱和渗流状态

该研究还提出，河流和地下水之间出现非饱和区，主要是受河床弱透层的影响，如果河床弱透层厚度很小，且饱和渗透系数和含水层的很接近，既是水头差很大，河流和含水层也不会出现非饱和水流，河流渗漏量是潜水面位置的函数。这与目前的研究是不符的，我国水文地质学家李俊亭［17］(1990)根据野外和室内的实验资料指出，即使河床下没有明显的隔水层，在一定的水力坡度条件下，地下水和河流也会失去直接水力联系，在河床下产生包气带，此时河流渗漏量达到最大值并保持不变，因此河流对地下水的补给能力也绝不是无限的。

Garey A.Fox和 A. M.A.ASCE［18］(2007)采用 MODFLOW软件的RIVER模块对上述河流地下水关系演化三个阶段，即 saturated flow(one－regime)、transition flow(two－regime)、unsaturated gravity－driven hyporheic zone flow(three－regime)进行模拟。模拟结果得出:当河水很浅、河床厚度很小、或含水层介质的进气压力水头值很大时，transition flow的影响就不可忽略。当河水深增加，河床渗漏量增大时，由负压值引起的渗漏增量相对较小，所以此时two－regime模型和three－regime模型计算结果的差异就很小。当河床弱透层厚度较大时，地下水位较小的降深就能使得河流补给量达到稳定状态，所以这种情况下，two－regime模型和 three－regime模型的计算结果也就相差很小。当河床弱透层渗透系数增大时，弱透层与含水层渗透系数的比值增大趋于1，饱和流和非饱和流的差异减小，transition flow的影响也就减小。同时当进气压力水头值较大时，在重力驱动下的非饱和流就对应一个较大的最大毛细压力水头，此时负压和transition regime就会更加显著。所以在计算河流和地下水转化时，有两种情况必须考虑transition regime的影响:①地下水位的降深刚好使得河流和地下水处于饱和和非饱和的过渡状态;②进气压力水头大，河床弱透层孔隙度小。

3 国内研究现状

刘国东、李俊亭［19］(1997)进行了傍河强开采机理研究。该研究建立一个垂向二维砂槽模拟傍河强采地下水的实验模型，根据饱和 －非饱和渗流理论，建立数学模型求解。研究结果表明，实验剖面上的浸润曲线是一条下凹曲线，并且随着傍河抽水强度的增大，曲线的下凹程度增大，直至河水与地下水产生脱节;脱节点不是紧接着河床的，而是河床下面的某一个位置，河床下产生悬挂饱水带。在之后的几年里，刘国东、李俊亭等人又对该过程做了更深一步的研究［20］，用数值模拟的方式验证实验结果，并模拟不同介质、不同水位动态下河流和地下水的水力联系。研究发现，由于悬挂饱水带的存在，河流地下水脱节后，河流通过悬挂饱水带仍以“渗入式”补给地下水，这说明之前学术界普遍认为的“淋滤式”补给在描述河流地下水脱节后的水流运动机理上是不准确的;并且当河水越浅、含水层渗透性越强，临界脱节的排泄水位就越高，河流与地下水就越容易脱节。但是该工作对上边界条件及包气带中致密层(涉及河流对地下水补给的影响带)的作用没有进一步研究，所以所提出的模型对解决实际问题还有一定的困难［21］。

钱会、郑西来等人［22］(1999)以非完整河(渠)旁完整井列抽水的理想化模型为基础，建立起该模型的三维稳定渗流数学模型(图10)，采用了有限差分法求解了不同情况下模型的数值解。他们得出，在非完整河(渠)旁抽取地下水会产生越河(渠)渗流问题，而且河流(渠)的宽度、河流(渠)的完整性以及河底弱透水层的渗透性都会对越河渗流问题产生重要的影响。这说明在求解这类傍河非完整井抽水问题时应采用三维渗流数学模型，因为对于未切割到隔水底板的非完整河流来说，河流两侧的地下水通过河流底部含水层的连接，已经成为一个相互联系的整体，当在河流的一侧抽水时，河流另一侧的地下水运动状况必定会影响到。所以，以往的地下水水源地计算过程中把不完整河流及其下部的含水层作为给定水头边界是不妥的。

蒋业放、张兴有［23］(1999)建立了河流含水层相互作用水力耦合模型。该模型是在分析河水与地下水相互作用规律的基础上，将河水运动模型、河水与地下水水量交换模型以及地下水运动模型三者耦合。其中河流模型采用忽略河槽调蓄作用的圣维南连续方程，含水层模型为潜水二维渗流方程，然后二者再通过动态水量交换机制实现耦合。水量交换模型分别模拟含水层顶托排泄、河流压力渗漏和淋滤渗漏等不同方式的水量转换过程。最后分别用欧拉法和三角网格差分法来求解河水模型和地下水模型。将该模型应用于实际问题后发现，耦合模型能较准确地模拟河流地下水系统的水量平衡与动态变化过程，能有效避免地表水和地下水水量的重复计算，可作为河水与地下水相互作用地区水资源评价、规划与管理以及地表水、地下水联合调度的模拟。但是该模型在计算河流和地下水转化量时，只是简单的将该过程概化为垂向一维水流运动，而实际过程中的水流转化都是三维或垂向二维的，这样的简化就使得计算结果相对不够准确。

图10 越河渗流示意图

潘世兵、王忠静等［24］(2002)做了关于河流和地下水转化量的研究，提出了一种新的模拟预测方法。它将河流越流系数做适当处理后用来表示河流和地下水的转化量，然后再将转化量计算模型同三维地下水数值模型完全耦合，以预测在有人工开采或补给条件下，地表水与地下水转化量的变化趋势。该方法适合多含水层系统的情形。

王文科(2011)等人［25］通过室内砂槽试验，模拟了在六种在不同试验方案下，河流向地下水转化的水动力过程。文中指出通过试验模拟，影响河流与地下水关系演化过程的主要因素有河水位的变化、地下水潜水面的下降、河床形状，河床弱透层及含水层介质。文中还重新定义了河流与地下水脱节的概念，认为河流和地下水脱节是发生在地下潜水面降低至河床下悬挂饱水带以下，并与其之间存在明显的包气带时，以及脱节后河床下悬挂饱水带形状特点，临界脱节时的水利条件等。

4 目前研究中存在的问题及研究展望

综上分析，以及实际试验可以得出，随着地下水的开采，地下水位持续下降，河流补给量随之增大。但是，河流对地下水的补给不是无限增大的，当补给量增大到一定程度以后，就不再增大，此时河流和地下水之间就会失去直接水力联系，地下水流不再是连续的饱和水流，在河床下部出现非饱和区，河床周围有悬挂饱水带。河流与地下水系统转化为河床下悬挂饱水带—包气带—饱水带的水流系统;对于含水层是非均质有弱透层的情况，地下水渗流受阻，问题就更加复杂，是河床下悬挂饱水带—包气带—上层滞水—相对隔水层—包气带—饱水带的水流系统。此时的河流边界也已经不是传统意义上的定水头边界，而转变为二类定流量边界。如果河床淤积，河床周围有弱透层，河流就是一个饱和 －非饱和系统的定流量边界。河床下相对致密层越多，水流状态越复杂，甚至会出现多层上层滞水现象。这对已有模型的仿真性就提出了更高的要求。

由于傍河抽水驱动下河流与地下水位关系的演化是一个由河流与地下水具有统一浸润曲面向不具有统一浸润曲面的转化过程。因此，采用饱和—非饱和流理论，研究河流与地下水关系的演化应该是很自然的事，但目前仍有许多问题尚待研究:

(1)关于饱和—非饱和的上边界问题;

(2)如何利用有限的野外数据获得较多的模型运转所需要的参数;

(3)高效的数值模拟算法;

(4)河床下薄层相对细粒堆积层和河床下非均质性对河流与地下水关系演化的影响;

(5)河床性质及其对河岸渗流效力的影响，河流入渗速率的确定;

(6)河流与地下水双向交换带物理化学和生物作用机理以及对河岸和地下水生态功能的影响等。

由此可见，河流与地下水之间关系演化的动力学机制和数值仿真模拟研究是亟待深入开展研究的前沿领域，是水文地质研究中的一个重要命题。从实际应用层次开展此项研究，可提高河流与地下水关系演化规律的仿真性以及沿河地段地下水资源评价的可靠性，为设计合理的傍河地下水开发方案以及生态环境保护提供科学依据;在理论上以饱和—非饱和流耦合分析有助于人们对沿河地带多孔介质中渗流模式、水份运移机制及渗流基本规律的认识，揭示河流与地下水关系演化过程，深化沿河地段地下水资源形成的认识，对发展与创新河床下地下水运动的理论和研究方法等具有十分重要的理论和实际意义。

［1］Theis，C.V. The relationship between the lowering of the piezometric surface and the rate and duration of discharge form a well using ground water storage［J］. Transactions of the American Geophysical U-nion1935.(2)，519 －524.

［2］Theis，C.V. The effect of a well on the flow of nearby stream［J］.American Geophysical Union Transactions 1941.22，no.3:734 －738.

［3］郭东屏.地下水动力学［M］.西安:陕西科技出版社.1995:170－174.

［4］Hantush，MS. Well near streams with semipervious beds［J］. Journal of geophysical research 1965，70.no.12:2829 －2838.

［5］Hunt. B. unsteady stream depletion from ground water pumping［J］.Ground Water;1999.37，no.1:98 －102.

［6］Garey A.Fox，Paul Duchateau，and Deanna S.Durnford. Analytical Model for Aquifer Respons Incorporating Distributed Stream Leakage［J］.Ground Water;Jul/Agu2002，378－384.

［7］Yakup Darama. An analytical solution for stream depletion by cyclic pumping of wells near streams with semipervious beds［J］. Ground Water;jan/feb2001:79－86.

［8］Jurgen Shubert. Hydraulic aspects of riverbank filtration—field studies［J］. Journal of Hydrology 2002(266)145 － 161.

［9］Xunhong Chen，Longcang Shu.stream －aquifer interactions:evaluation of depletion volume and residual effects form ground water pumping［J］. Ground Water;May/Jul 2002，284 － 290.

［10］Sushil K.Ssingh，Govind C.Mishra，et al. Aquifer diffusivity and stream resistance from varying stream stage［J］. Journal of irrigation and drainage engineering，January/february 2002:57 －61.

［11］Mohamed M.Hantush.Modeling stream – aquifer interactions with linear response functions［J］. Journal of Hydrology 2005(311)59–79.

［12］Riesenauer AE. Methods of solving problems of multidimensional，partially saturated steady flow in soils［J］. J Geophys Res 1963，68(20):5725－5733.

［13］Peterson DM，.Wilsion JL.Variably saturated flow between streams and aquifers［J］. Tech Completion. Socorro:New Mexico Water Resources Research Institute，1988:233－356.

［14］Stephen DB. Vadose zone hydrology. Boca Raton:CRC Press－Lewis Publisher，1996.

［15］Bouwer H，Maddock T. Making sence of the interaction between groundwater and streamflow lessons for watermasters and adjudicator［J］. Rivers1997，6(1):19 －31.

［16］Fox G.A. D.S.Durnford. Unsaturated hyporheic zone flow in stream/aquifer conjunctivesystems［J］. Advances in Water Resources2003，26:989－1000.

［17］李俊亭.河流补给机理的实验研究［R］.西安:西安地质学院.1990.

［18］Garey A.Fox，A. M.ASCE and Leili Gordji. Consideration for unsaturated flow beneath a streambed during alluvial well depletion［J］. Journal of Hydrology engineering;march/april2007:139 －145.

［19］刘国栋，李俊亭.傍河强采地下水的渗流机理研究［J］.中国科学.1997，27(4):375 －380.

［20］刘国东，李俊亭，等.地下水与河水脱节的实验与模拟［J］.水文.1999(3):10－15.

［21］王文科，李俊亭，王钊，等.河流与地下水关系的演化及若干科学问题［J］.吉林大学学报.2007，37(2):231－238.

［22］钱会，郑西来，樊秀峰.傍河取水越河稳定渗流问题的三维数值模拟研究［J］.水力学报.1999(3):32－37.

［23］蒋业放，张兴有.河流与含水层水力耦合模型及其应用［J］.地理学报.1999，54(6):526 －533.

［24］潘世兵，王忠静，邢卫国.河流－含水层系统数值模拟方法探讨［J］.水文.2002，22(4):19 － 21.

［25］Wang，W.K.，2011.Evolution of stream －aquifer hydrologic connectedness during pumping－ Experiment. Journal of Hydrology 402，401－414.

Research Progress and Existing Problems about the Numerical Simulation Study on the Evolution of Stream－Groundwater Relationships during Pumping

YAO Ke － jun1，WANG Wen － ke2，WANG Shi－ dong1
(1.Xi＇an Research Institute of China Coal Technology ＆ Engineering Group Corp，Xi’an 710054，Shaanxi;2.School of Environmental Science and Engineering，Chang’an University，Xi’an 710054，Shaanxi)

The evolution of the hydrologic relationship between streams and aquifers resulting from groundwater pumping(or drainage)near a stream is of great theoretical and practical significance to deepening understanding of the formation of groundwater resources along the river lots，and also to develop and innovate the groundwater movement theory and research methods. The paper is based on data analysis from home and abroad，sums up study progress and defects of analytical solution and the numerical solution of the numerical simulation model on the evolution of stream－groundwater relationships during pumping，and puts forward to the complexity of the actual situation and research direction of the problem.

The numerical simulation study，Pumping near a stream，Stream －aquifer interaction，Evolution of stream －groundwater relationship and Research progress

TV211.1+2

A

1004－1184(2012)05－0001－06

2012－05－11

国家自然科学基金项目(40472131)—河流与地下水关系演化的动力学机制与仿真模拟

姚珂君(1984－)，女，陕西西安人，工程师，主要从事地下水数值模拟及煤矿防治水研究。