一维地下水非稳定流计算的配点法

王佳慧，周德亮，李 静

(辽宁师范大学 数学学院，辽宁 大连 116029)

一维地下水非稳定流计算的配点法

王佳慧，周德亮，李 静

(辽宁师范大学 数学学院，辽宁 大连 116029)

传统的地下水数值计算方法(如有限元法和有限差分法)都需要网格或单元，网格生成需要占用大量的计算时间，求解所需数据量也较大。配点型无网格法摆脱了网格和单元的限制，只需节点信息，且节点布置灵活，易于实施。本文将配点型无网格法应用于解决一维地下水非稳定流计算问题，用MATLAB编制相应的程序，将结果与解析解和传统方法的计算结果相比较，计算得到的结果与解析解吻合很好，精度较高，计算过程简单，稳定性好。

径向基函数 配点法 一维非稳定流 地下水数值模拟

非稳定水流现象在水利工程中广泛存在，河道或河网的水流或洪水波运动，溃坝后向下游传播的涌波，闸门启闭后的水波运动等，这些都属于非稳定水流运动，是水利水电工程和海岸工程中经常遇到且需要解决的问题［1］。非稳定水流数学模型在水利工程中有广泛的应用价值，研究非稳定流数值模型的目的在于建立稳定、精度较高、计算储存量和计算耗时较少的高效计算格式。

目前解决非稳定流计算主要采用有限元法和有限差分法，但是这两种方法有一个共同的特征是它们需要生成网格再进行计算。由于网格的存在，生成网格的好坏，会直接影响到数值求解的成败［2］。实际问题中网格生成要耗费大量的时间，应用中会遇到很多困难。而配点型无网格法可以很好的解决传统方法存在的缺陷。本文结合前人的无网格法研究成果，得到一维非稳定流配点型无网格法的计算格式。

1 径向基配点法求解一维非稳定流计算

无网格法(Meshless methods)是在建立整个问题域的系统代数方程时，不需利用预定义的网格信息域离散的方法。无网格法利用一组在问题域中以及域边界上的节点表示(而非离散)该问题域和其边界。这组散布的节点被称为节点，它们并不构成网格，通过这些节点上的值拟合出一个逼近函数［2］。该函数有较好的光滑性而且导数连续，这样不仅摆脱了网格的约束，避免了复杂的网格生成及重新划分工作，而且提供了连续性好，形式灵活的基函数。这种方法在地下水数值计算中具有一定的灵活性，此外还有精度高，前后处理较有限元法和有限差分法简便等特征［3］。现有的无网格法基本上可分为Galerlin型和配点型两大类。Galerlin法虽具有良好的稳定性和精确性，但需要布置背景无网格进行数值积分，计算量较大，配点型无网格法可以很好地解决这一问题［4］。配点型无网格法离散系统代数方程的过程直接，且实现其离散方程的算法简洁，不需要数值积分。

1.1 一维非稳定水流模型

考虑如下一维地下水非稳定渗流问题

其中，H(x，t)为水头，T(x)=KM 为导水系数，k(x)为渗透系数，M为含水层厚度，S(x)=SsM为贮水系数，Ss为贮水率，w(x，t)为源汇项，h0(x)、g(x，t) 、q9x，t)为给定的函数，［a，b］为渗流区域，a，b，［a，b］为区域 的边界。

1.2 径向基函数

径向基函数(Radial Basis Function，简记 RBF)是以动点与定点 的欧几里德距离为自变量的一元函数φj(x)=φ(‖x－xj‖)。对任意函数u(x)，可以用径向基函数近似为

其中 N表示节点总数，xj为在 Ω上布置的节点，αj为待解系数。

1.3 用配点法数值计算

在区域［a，b］及其边界上配置节点 x1，x2，…，xN，其中x1，x2，…，xN0为区域［a，b］内部节点，xN0+1，xN0+2为边界节点，N0和2分别为内节点和边界节点数，总节点数为 N=N02。

用径向基函数逼近 H(x，t)n，即

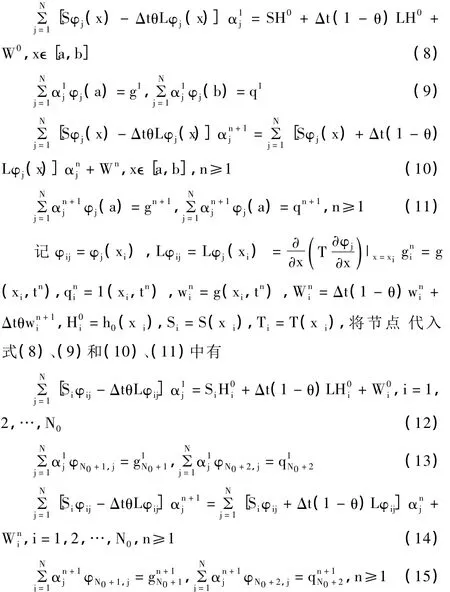
首先由(12)和(13)确定的线性方程组中解出 α1n+1，，…，再由线性方程组(14)和(15)中逐层解出 ，代入(7)中即得到水头函数 离散的近似解。

2 算例分析

算例1图1是右河水位突变时河间地块承压水一维非稳定流运动的例子。参数和定解条件都在图1中，控制方程为:

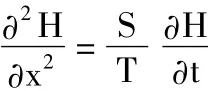
图1 河间地块承压水非稳定运动的例子(根据 H.F.王和.M.P.安德森)

本问题的解析解已由根据 H.F.王和.M.P.安德森给出，采用本文介绍的径向基函数配点法和有限差分法对其求解。应用MATLAB软件，分别用有限差分法和径向基函数配点法编制相应的计算程序，计算时取空间步长 ，时间步长 ，将程序运行后的解析解，RBF解和差分解制成表格，为避免占用大量的空间，本表制作时只选用部分时间点的数据。见表1。

表1 解析解，RBF解和差分解表

3 结论

采用径向基函数配点法计算一维非稳定流地下水问题是有效的，能够排除网格划分对它的影响，既可以节省计算量又能保证精度。程序运行后，配点法求出的解析解与精确解吻合良好，且计算精度高于有限差分解。采用MATLAB软件编制程序时，用径向基函数配点法的编制过程较用有限差分法程序的编制过程简单。本文介绍的是径向基函数配点法在一维非稳定流中的应用，有关这种方法在二维流和三维流的应用限于篇幅将另文论述。

［1］薛禹群，谢春红.地下水数值模拟［M］.北京:科学出版社，2007.

［2］LIU G R，GU Y T.无网格法理论及程序设计［M］.王建明，周学军，译.济南:山东大学出版社，2007.

［3］周德亮，王焕丽.径向基函数法在地下水模拟中的应用［J］.辽宁师范大学学报:自然科学版，2008，31(4):390－392.

［4］张宏伟，李美香，李卫国.关于配点型无网格法边界条件处理技术［J］.大连理工大学学报，2010(7)，50(4):614－618.

The Collocation Meshless Method in Simulation of One－Dinensional Non－steady Flow

WANG Jia － hui，ZHOU De － liang，LI Jing
(School of Mathematics，Liaoning Normal University，Dalian 116029，Liaoning)

Traditional groundwater numerical methods(such as finite element and finite difference method)require grid or unit，mesh generation would take a lot of calculation time，a large amount of data needed to solve. The collocation meshless method get rid of the grid and unit limitation and only need node information and node layout flexible and easy to implement.In the paper，with collocation meshless method will be applied to solve the one－dimensional non－steady groundwater flow calculation problem，the preparation of the corresponding program，the results with analytical solutions and traditional methods of calculation compared to the calculated results in good agreement with the analytical solution，more accurate than high，the calculation process is simple，good stability.

RBF;Collocation method;One－dimensional non－steady flow and Numerical simulation of groundwater

P641.2

A

1004－1184(2012)01－0042－03

2011－10－14

王佳慧(1986－)，女，吉林四平人，在读硕士研究生，主攻方向:偏微分数值解法。