钢桁梁桥上无缝线路空间耦合模型研究

曲 村，高 亮，蔡小培，车宏军

(1.北京交通大学土木建筑工程学院，北京 100044;2.沈阳中铁交通设计咨询有限公司，辽宁沈阳 110013)

钢桁梁桥由桁架杆件组成，桁架杆件主要承受轴向力。与实腹梁相比，钢桁梁桥用腹杆代替整体的腹板，从而节省了钢材并减轻了结构自重。钢桁梁桥可做成较大高度，具有较大的刚度及跨度，在我国很多跨越大江大河的铁路线上使用［1］。

由于钢桁梁桥的桥梁结构和桥上轨道结构具有特殊性，简单的桥上无缝线路计算模型并不适用。参与钢桁梁桥上无缝线路传力作用的主要部件有钢轨、扣件、轨枕(包括木枕和混凝土枕)、道床、钢桁梁(包括纵梁、横梁、桁杆)、桥墩等。本文在已有研究的基础之上［2-8］，以某单线铁路上钢桁梁桥上无缝线路为例，采用有限元方法单独建立了钢桁梁桥上无缝线路纵横垂向空间耦合模型，对各部件利用ANSYS单元模型分别进行模拟。

1 主要计算参数选取

该钢桁梁桥桥梁形式为8×33.7 m栓焊简支桁梁。固定支座全部设于同一方向。根据设计资料整理得到一跨桁架梁的杆件编号及相应断面，如图1和图2所示。各桥墩的墩顶纵向刚度见表1，其中0号墩和8号墩分别为两侧桥台。

图1 桁杆编号

钢轨为60 kg/m钢轨，两端桥头路基为碎石道床，铺设Ⅲ型轨枕和弹条Ⅱ型扣件，纵向阻力取91 N/cm。钢桁梁桥上铺设木枕，采用K型分开式扣件，按1紧+n 松 +1 紧布置，按 n分别取值为0，1，2，3，4 进行计算，扣件纵向阻力取值参照表2。

根据文献［9］规定，计算伸缩力时，钢桥的温差取25℃;计算挠曲力时，采用设计荷载“中—活载”。

2 空间耦合模型的建立

2.1 钢轨及扣件模型

钢轨选用梁单元BEAM188进行模拟，按照实际截面属性建模，考虑截面积、惯性矩、扭转弯矩等参数。钢轨按照支承节点划分单元，可全面考虑纵向、横向、垂向线位移及转角。扣件采用弹簧单元进行模拟，可全面考虑扣件的纵向阻力、横向阻力和垂向刚度。扣件的阻力和刚度值均根据实测值选取。

图2 各桁杆截面(单位:mm)

表1 钢桁梁桥各桥墩墩顶纵向刚度

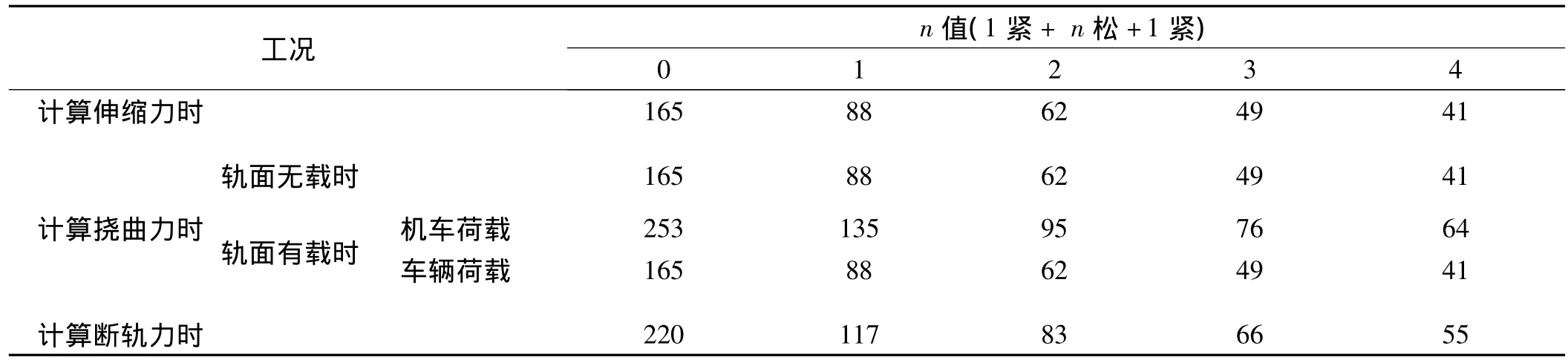
表2 不同布置方式扣件纵向阻力 N/cm

2.2 轨枕模型

轨枕选用梁单元BEAM188进行模拟，考虑截面积、高度、惯性矩等实际参数，按照较小间距的支承节点划分单元，可全面考虑纵向、横向和垂向线位移及转角。两端桥头路基上道床的纵、横向阻力和垂向支撑刚度采用弹簧单元进行模拟，阻力和刚度值根据实测值取值。路基上与钢桁梁桥上采用的不同类型轨枕结构，间距也有所不同。

2.3 钢桁梁桥模型

钢桁梁桥各桁杆采用梁单元BEAM188进行模拟，可以全面考虑钢桁梁桥的结构组成以及各根桁杆、纵梁、横梁等的几何尺寸、截面形状和物理属性。钢轨与木枕之间相互连接的扣件，以及木枕与桁梁之间相互固定的螺栓均采用弹簧单元进行模拟。

2.4 整体空间耦合模型

由以上各部分组成的钢桁梁桥上无缝线路整体空间耦合模型如图3所示。

3 钢桁梁桥上无缝线路附加力计算

本文中钢桁梁桥上无缝线路纵向附加力的计算，共涉及8跨33.7 m简支钢桁梁桥，计算结果均考虑了相邻桥跨产生的影响。当K型分开式扣件布置方式为1紧+0松+1紧时，钢轨的伸缩力和位移计算结果分别如图4和图5所示。

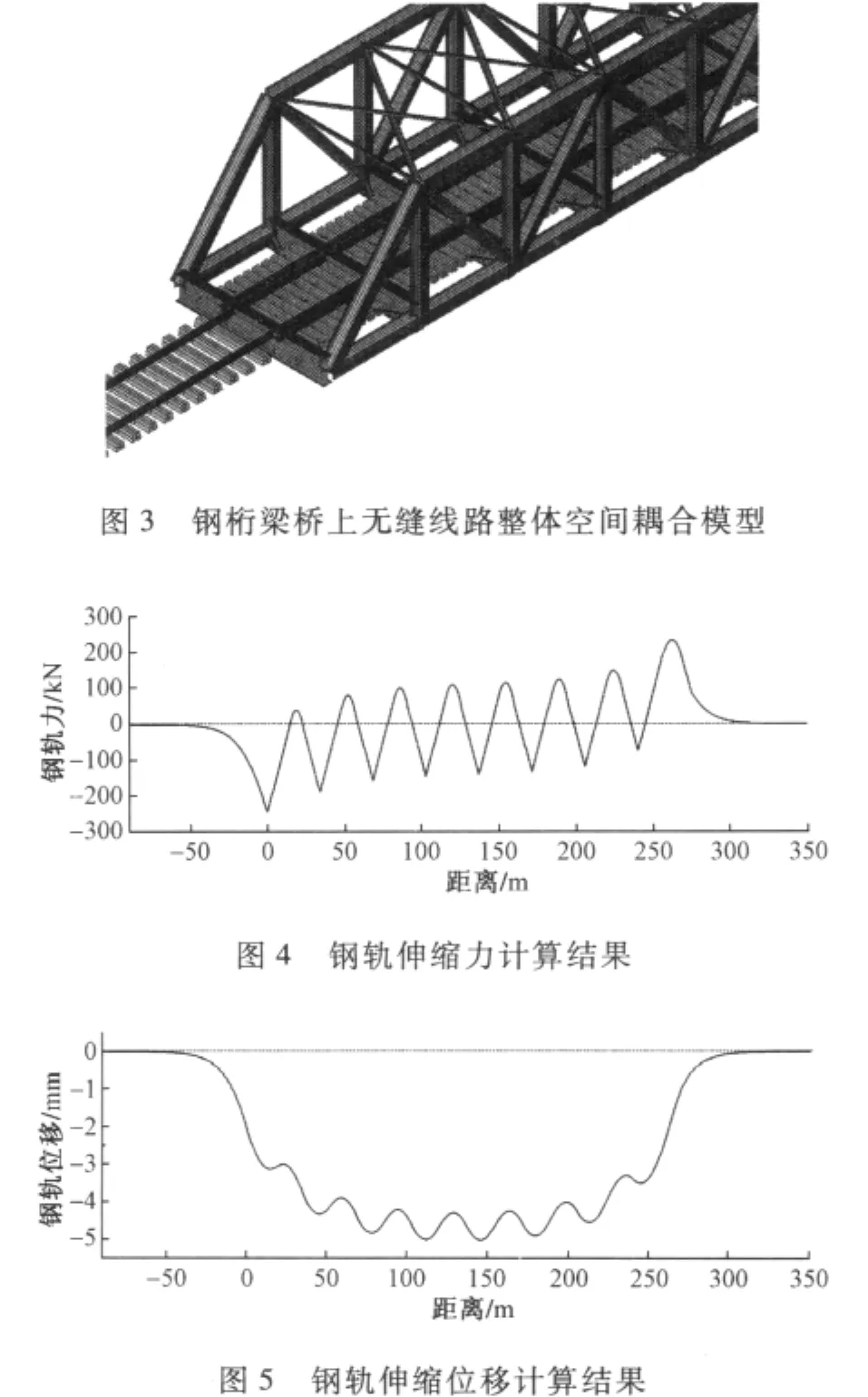
采用不同的K型分开式扣件布置方式时，桥梁的伸缩力计算结果比较如图6所示。由图6可知，随着钢桁梁桥上扣件布置方式的变化，即扣件阻力的减小，钢桁梁桥上无缝线路钢轨伸缩附加力也随之变小。

采用不同扣件布置方式的钢桁梁桥上无缝线路的钢轨和桥墩受力计算结果见表3。

图6 钢轨伸缩附加力随扣件布置方式变化

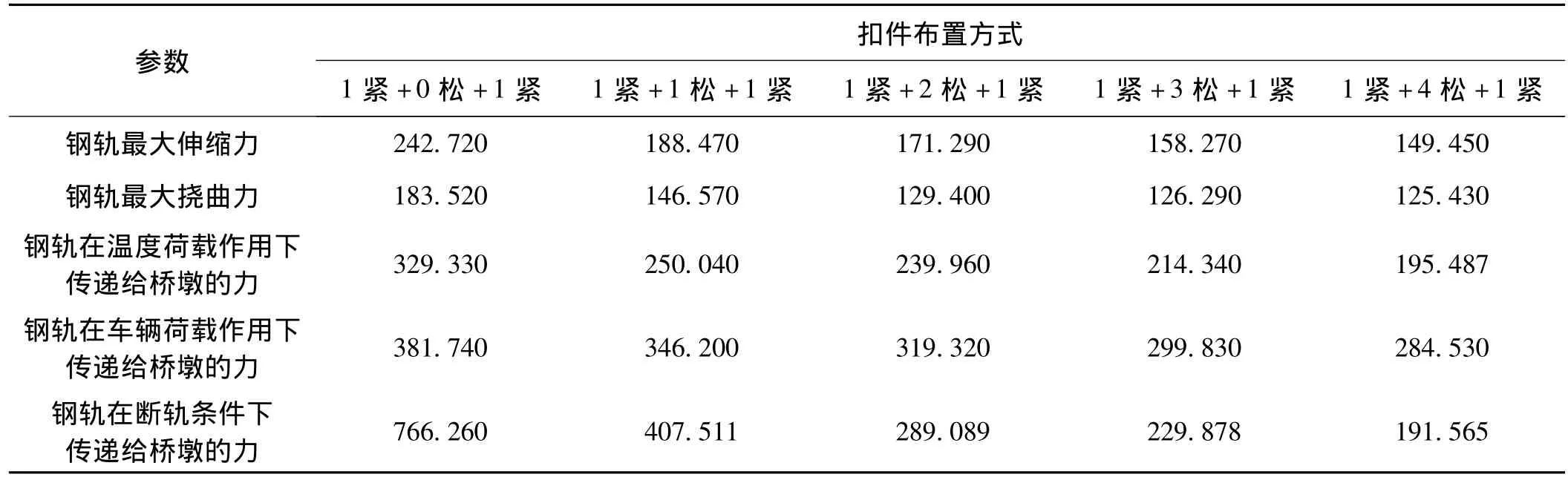
表3 钢桁梁桥上无缝线路钢轨和桥墩受力计算结果 kN

由表3可知，随着钢桁梁桥上扣件布置方式的变化，即扣件阻力的减小，钢桁梁桥上无缝线路钢轨最大伸缩附加力和挠曲附加力、钢轨在温度荷载、车辆荷载作用下及断轨条件下传递给桥墩的力都随之变小。

4 钢桁梁桥上无缝线路变形计算

4.1 温度荷载作用下梁缝纵向变化量

在温度荷载作用下，钢桁梁桥产生伸缩变形，梁端处变形量较大时会造成梁缝纵向变化量过大，严重时可能会影响到梁端处的扣件间距及轨道结构的稳定性。钢桁梁桥梁缝纵向变化量计算结果见表4。

在本文所采用的温度荷载作用下，简支梁梁缝处的最大变化量为10.635mm。较大的梁缝变化量可能对梁端处木枕与纵梁间相互固定的螺栓造成不利影响，应加强关注，以防止螺栓失效造成梁端处轨道结构失稳。

4.2 温度荷载作用下钢轨横向变形量

在温度荷载作用下，不同扣件布置方式下的钢轨横向变形量见表5。由表5可见，当K型分开式扣件布置方式为1紧+0松+1紧时，钢轨轨距变化量最大值为0.212mm，轨距变化率最大值为0.222‰，轨向变化量最大值为0.260mm，轨向变化率最大值为0.206‰。

表4 钢桁梁桥的梁缝纵向变化量 mm

表5 钢桁梁桥的钢轨横向变形量

根据文献［10］规定，时速不超过120 km/h时，无砟轨道线路的静态平顺度限值为:轨距变化量+3/-2 mm，轨向变化量4 mm，轨向变化率即4 mm轨向变化量与10m测量弦长之比为0.4‰。所计算的各项轨道横向几何形位变化值皆满足规范规定。

但在长期使用和车辆荷载的作用下，钢轨横向变形量有可能进一步加大，因此也应加强对两端桥头路基与钢桁梁桥过渡处及钢桁梁桥之间的轨道横向几何形位的关注，防止其变形超限，影响行车安全与旅客舒适度。

4.3 车辆荷载作用下桥梁竖向挠度

根据文献［11］，简支钢桁梁的桥跨结构由于列车竖向静活载所引起的竖向挠度不应超过容许值L/900，其中L为简支钢桁梁检算跨的跨度。即33.7 m简支钢桁梁桥的挠度最大不应超过37.4 mm。不同扣件布置方式下的桥梁挠度见表6。

表6 钢桁梁桥的桥梁竖向挠度 mm

由计算可得，当“中—活载”布设在不同的桥跨位置时，桥梁的最大挠度为28.163 mm，满足规范规定。由于计算时采用的“中—活载”较实际车辆荷载大得多，因此本文所建立的钢桁梁桥在机车车辆荷载作用下的挠度有一定的安全储备。

5 结论及建议

1)本文所建立的钢桁梁桥上无缝线路纵横垂向空间耦合模型，充分考虑了钢轨、扣件、轨枕(包括木枕和混凝土枕)、道床、钢桁梁桥(包括纵梁、横梁、桁杆)，以及桥墩台等对整体力学特性的影响，可以更详细地进行计算和检算。采用该模型可以计算钢轨及桥墩在温度荷载和车辆荷载作用下所产生的附加力，也可以对梁缝纵向变化量、钢轨横向变形、桥梁竖向挠度等进行计算，便于设计与施工应用。

2)在本文所建模型和采用的参数条件下，随着钢桁梁桥上K型分开式扣件布置方式的变化，即扣件阻力的减小，钢桁梁桥上无缝线路钢轨最大伸缩附加力和挠曲附加力、钢轨在温度荷载、车辆荷载作用下及断轨条件下传递给桥墩的力都随之变小，钢轨横向变形量也随之减小，而梁缝纵向变化量和桥梁竖向挠度的最大值则随之增大。

3)在温度荷载作用下，钢桁梁桥之间较大的梁缝变化量可能对梁端处木枕与纵梁间相互固定的螺栓造成不利影响，或使扣件抗拔力超限，应加强关注，以防止螺栓或扣件失效造成梁端处轨道结构失稳。

4)在温度荷载作用下，钢桁梁桥上的钢轨会产生一定的横向变形，应加强对两端桥头路基与钢桁梁桥过渡处及钢桁梁桥之间的轨道横向几何形位的关注，防止其变形超限，影响行车安全与旅客舒适度。

［1］裘伯永，盛兴旺.桥梁工程［M］.北京:中国铁道出版社，2003.

［2］杨艳丽.钢桁梁桥上无缝线路附加力分析［J］.铁路工程造价管理，2005，20(1):30-32.

［3］潘志明.铁路钢桁梁桥状态评估［J］.桥梁建设，2006(增1):143-145，149.

［4］陈鹏，高亮，冯雅薇，等.连续梁桥上无缝线路纵向附加力的变化规律［J］.北京交通大学学报，2007，31(1):85-88.

［5］陈鹏，高亮，马鸣楠.空间钢桁梁桥上无缝线路梁轨相互作用耦合模型［J］.钢结构，2007，22(10):28-30.

［6］何旭辉，余志武，陈政清.既有铁路钢桁梁桥基准有限元模型建立与验证［J］.振动与冲击，2007，26(12):117-121.

［7］曲村，高亮，乔神路，等.高速铁路长大桥梁CRTSⅠ型双块式无砟轨道无缝线路影响因素分析［J］.铁道工程学报，2011(3):46-51，63.

［8］曲村，高亮，乔神路.高速铁路长大桥梁CRTSⅠ型板式无砟轨道无缝线路力学特性分析［J］.铁道标准设计，2011(4):12-16.

［9］中华人民共和国铁道部.铁建设函［2003］205号 新建铁路桥上无缝线路设计暂行规定［S］.北京:中国铁道出版社，2003.

［10］中华人民共和国铁道部.TB 10082—2005 铁路轨道设计规范［S］.北京:中国铁道出版社，2005.

［11］中华人民共和国铁道部.TB 10002.1—2005 铁路桥涵设计基本规范［S］.北京:中国铁道出版社，2005.

［12］徐金辉，王平.大跨度中承式拱桥桥上无缝线路计算分析［J］.铁道建筑，2011(10):92-94.

［13］徐井芒，刘丹，王平.大跨度尼尔森体系钢筋提篮拱桥桥上无缝线路计算分析［J］.铁道建筑，2011(11):122-124.