基于混凝土无应力计测值统计模型反演热膨胀系数

唐腾飞，黄耀英，周宜红，周绍武，李金河，景 继，程中凯

（1.三峡大学水利与环境学院，湖北 宜昌 443002；2.中国长江三峡集团公司，湖北 宜昌 443002）

0 引 言

对于混凝土而言，温度变形是材料热胀冷缩引起的变形；湿度应变是混凝土因湿度变化而引起的变形；自生体积应变是由于水泥水化热和其他一些未知的物理化学变化引起的，其变化规律比较复杂。温度变形、湿度变形和自生体积变形都是自由体积变形，在实际混凝土工程上，一般采用无应力计来监测[1-2]。对无应力计测值进行分析时，一般选取降温时段的无应力计测值的变化量和温度测值的变化量来获得热膨胀系数，然后再分离出自生体积变形。由于自生体积变形变化规律比较复杂，有些混凝土工程的自生体积变形需要较长时间才能趋于稳定，这导致采用不同的降温时段反演获得的热膨胀系数具有较大的差异，甚至是采用同一降温时段，如采用中冷、二冷期间不同的降温过程线，反演获得的热膨胀系数也具有一定的波动性。热膨胀系数的差异直接导致分离的自生体积变形的不合理性。

大坝监测数据受到多种因素的复杂影响并存在监测误差，具有不确定性，可看作是随机变量。采用数值统计法定量处理这些数据，建立大坝监测统计模型来揭示测值的变化规律是一种常用的方法[3-4]。由于无应力计测值由温度分量、自生体积变形和湿度变形等组成，通过建立无应力计测值的统计模型分离出温度分量和自生体积变形分量，无疑是一条较好的途径。本文探讨基于无应力计测值统计模型反演混凝土热膨胀系数以及分离自生体积变形分量。

1 混凝土热膨胀系数反演分析的基本原理

1.1 传统方法反演热膨胀系数

热膨胀系数可采用无应力测值反演获得。通过无应力计实测的自由应变可用下式表示

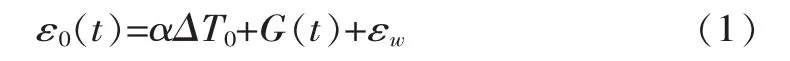
式中，αΔT0为温度应变，α为热膨胀系数；G（t）为自生体积变形；εw为湿度变形。

在一般情况下，混凝土的自生体积变形发生在早龄期，经过一段时间以后，变形将趋于平缓[5]。大体积混凝土内的湿度变化不大，由此认为，混凝土温度开始下降时，湿度变形变化不大。即认为混凝土内部温度下降时，有G（t）+εw≈0。此时，可以利用降温时段的无应力计的应变测值和温度测值来求得热膨胀系数。在实际分析时，常在混凝土的降温段取若干个无应力测值和相应温度值，采用最小二乘法来求得热膨胀系数。求得热膨胀系数后，将无应力计测值扣除温度分量，即可获得自生体积变形分量。

1.2 基于无应力计测值统计模型反演热膨胀系数

由混凝土自生体积变形的试验资料可知，一般初期自生体积变形变化大，随后呈单调递减趋势。参考朱伯芳院士提出的混凝土热学力学性能随龄期变化的组合指数公式[6]，本文采用3个指数公式累加来描述自生体积变形的变化规律。对于温度变形分量，则采用无应力计的温度作为因子，而大体积混凝土内的湿度变化不大，不另选因子，由此建立无应力计测值统计模型为

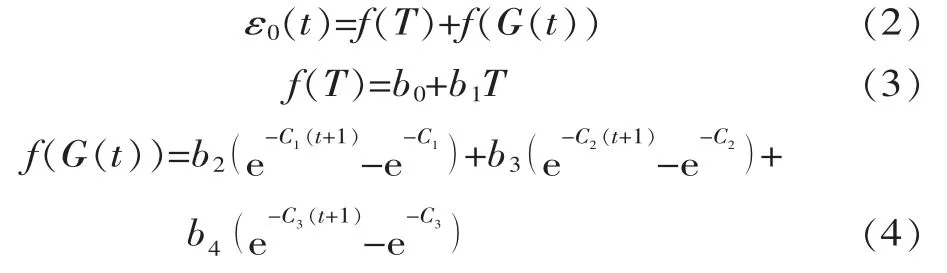
式中， f（T）为温度分量； f（G（t））为自生体积变形分量； bi（i=0，4）为回归系数； Ci（i=1，3）为常数， 根据回归经验，C1=0.3，C2=0.05，C3=0.005。

采用逐步回归分析法获得无应力计测值的统计模型回归系数后，自动分离出温度变形分量和自生体积变形分量，对比公式（2）和公式（1），可以认为系数b1即为热膨胀系数，即b1=α。

2 工程应用

2.1 工程实例

某建设中的水电站混凝土高拱坝位于四川省雷波县和云南省永善县接壤的金沙江峡谷段，是一座以发电为主，兼有拦沙、防洪和改善下游航运等综合效益的大型水电站。工程枢纽主要由拦河坝、泄洪、引水、发电等建筑物组成。拦河大坝为混凝土双曲拱坝，坝顶高程610 m，最大坝高285.5 m。左、右两岸布置地下厂房，各安装9台水轮发电机组，电站总装机1 386万kW，多年平均发电量571.2亿kW·h。大坝共31个坝段。为对大坝混凝土的应力应变进行监测，在坝体混凝土内埋设了无应力计和应变计组进行监测。

由于该高拱坝混凝土自生体积变形较大，一般为收缩形，且稳定时间较长，本文分别采用传统方法和无应力计测值统计模型反演热膨胀系数，以下选取典型无应力计NCP14-1和NZ18-3X进行分析。基于无应力计统计模型反演热膨胀系数时的回归系数见表1；2种方法反演的热膨胀系数见表2。实测值和拟合值对比见图1；分离自生体积变形对比分析见图2。另外，本文总共选取了15支无应力计，反演的热膨胀系数和分离出来的自生体积变形的稳定值见表3。

表1 统计模型回归系数

表2 典型无应力计反演热膨胀系数对比10-6℃

2.2 成果分析

（1）典型无应力计拟合值和实测值吻合效果良好，如无应力计NCP14-1的复相关系数为0.992，无应力计NZ18-3X的复相关系数为0.989，这说明本文建立的无应力计测值统计模型是可行的。

（2）由表2可见，采用传统方法反演混凝土热膨胀系数，选取的降温时段不同，反演得到的热膨胀系数差异较大。分析还表明，即使采用中冷和二冷降温期间的不同降温段，反演的热膨胀系数也存在一定的差异。而采用无应力计测值的统计模型反演的热膨胀系数相对稳定，反演的热膨胀系数综合反映了整个温度历程，反演的值更可靠。

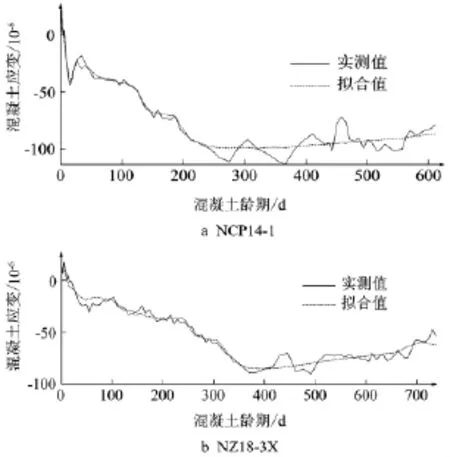
图1 典型无应力计实测值与拟合值对比

图2 典型无应力计分离出的自生体积变形计算值与拟合值对比

（3）由表3可见，基于无应力计统计模型分离出的自生体积变形平均值随时间逐渐趋于稳定，自生体积变形呈收缩形，稳定值的平均值大约为-40×10-6；反演的热膨胀系数为4.863 3×10-6～7.704 2×10-6℃， 热膨胀系数平均值为6.394 8×10-6℃。

3 结 语

（1）如果混凝土自生体积变形较大，且稳定时间较长，导致采用不同降温时段无应力计测值反演的热膨胀系数波动较大。

（2）建立了无应力计测值的统计模型，提出了基于无应力计测值统计模型反演混凝土热膨胀系数，以及分离自生体积变形分量。实践表明，该方法反演的混凝土热膨胀系数稳定性较好。

表3 反演的热膨胀系数和分离自生体积变形稳定值

（3）结合某建设中的高拱坝的无应力计测值，采用本文提出的无应力计测值统计模型反演的混凝土热膨胀系数平均值为6.394 8×10-6℃，自生体积变形呈收缩形，稳定值大约为-40×10-6με。

［1］吴中如.水工建筑物安全监控理论及其应用［M］.北京：高等教育出版社，2003.

［2］储海宁.混凝土坝内部观测技术［M］.北京：水利电力出版社,1989.

［3］李珍照.大坝安全监测［M］.北京：中国电力出版社，1997.

［4］吴世勇，陈建康，邓建辉.水电工程安全监测与管理［M］.北京:中国水利水电出版社，2009.

［5］朱伯芳，张超然.高拱坝结构安全关键技术研究［M］.北京：中国水利水电出版社，2010.

［6］朱伯芳.混凝土热学力学性能随龄期变化的组合指数公式［J］.水利学报， 2011， 42（1）:1-7.