多目标遗传算法和决策在船型论证中的应用

杨路春，李学斌，丁明君，黄利华

(1.上海交通大学船舶海洋与建筑工程学院，上海200240;2.武汉第二船舶设计研究所信息化技术中心，湖北武汉430064)

船型方案论证是船舶总体设计的重要内容，它依据船舶使用任务要求，从船型技术性能、经济性能、公约和规范等方面对设计方案进行论证，从可行方案中，依据评价指标和综合分析，选择技术与经济性能最佳的船型方案，使船舶获得良好的营运经济效益.这是一个复杂的多目标优化和决策问题，它的求解是一个不断改进和迭代的过程.

传统的船型论证方法有网格法和优化方法等［1］.网格法是根据船舶主尺度要素限制，在要素允许范围内系列变化设计变量，按照全组合的方式组成若干船型，对每个方案进行分析比较，依据船型评价指标排序择优.很多方法应用于评判和比较，如层次分析法(AHP)［2］、模糊综合评判［3］、数据包络分析［4］、人工神经网络［5］等.优化法则通过以主尺度范围、公约和技术规范等作为约束条件，以技术性能和经济性能的多个指标作为目标函数建立数学模型.对于船型论证这样一个复杂的多目标优化问题，往往是通过各种方法(例如加权法［6］、最小偏差法［7］、宽容度排序［8］等)把多个优化目标转换为单目标，然后得到最优解.

船型方案论证实际上包括2个过程:首先生成多个方案，然后再依据评估准则从中选择或者对这些方案排序.生成解的品质的优良与否，直接决定了后续选择的方案好坏，而评估和选择技术本身不能提高方案的质量.本文针对船型方案论证是一个典型的多目标优化和决策过程的特点，引入现代多目标遗传算法和决策技术进行探讨.建立了船型论证过程中的多目标数学模型，采用多目标优化算法(MOGA)获得多目标优化问题的解集.解集就对应备选方案，这些方案都是非劣解.依据距离理想解最近的方法对这些备选方案进行排序.文中讨论了一个内河集装箱船的论证算例，并且和常规的网格法、单目标优化方法的结果进行了对比，并提出了改进建议.

1 多目标优化问题和求解

工程实践中的很多优化问题都是多目标优化问题.通常多目标优化问题可以表示为

式(1)表示了n个优化属性准则，l个决策变量，I个等式约束和J个不等式约束的多目标最小化优化问题.

多目标优化问题中各个目标之间通常相互制约，其中一个目标的优化是以牺牲其他目标为代价的.与单目标优化问题不同的是，多目标优化问题的解通常不是唯一的，而是存在一个最优解集合，通常称为Pareto最优解.

20世纪80年代以后，出现了很多现代的进化算法，与传统求解多目标问题的算法相比，进化算法求解多目标优化问题最大的优点在于算法运行一次可以同时得到多个非劣解，进而构成非劣解集.

本文采用Fonseca和Fleming提出的对遗传算法的种群进行非劣分级的多目标遗传算法(multiobjective genetic algorithms，MOGA)［9］进行求解.该算法既强调非劣解同时又保持非劣解多样性.MOGA的独特之处是种群中每个解的适应值分配方式.为了保持非劣解中解的多样性，在每个等级的个体中引入了小生境数.距离尺度的计算利用的是目标函数值.在MOGA中使用了共享函数法，并将一个个体的适应值除以它的小生境数来得到它的共享适应值.尽管每一个等级的所有个体具有相等的指定适应值，但是位于较稀疏区域的个体具有更好的共享适应值.这样就对任何等级的没被充分表示的个体产生了更大的选择压力.将指定适应值除以小生境数降低了每个个体的适应值，为了保持每个等级的所有个体的平均共享适应值与平均指定适应值相同，对这些适应值进行尺度变换.此后，利用比例选择、单点交叉、基本位变异算子以产生新的一代.图1给出了MOGA算法的计算流程.

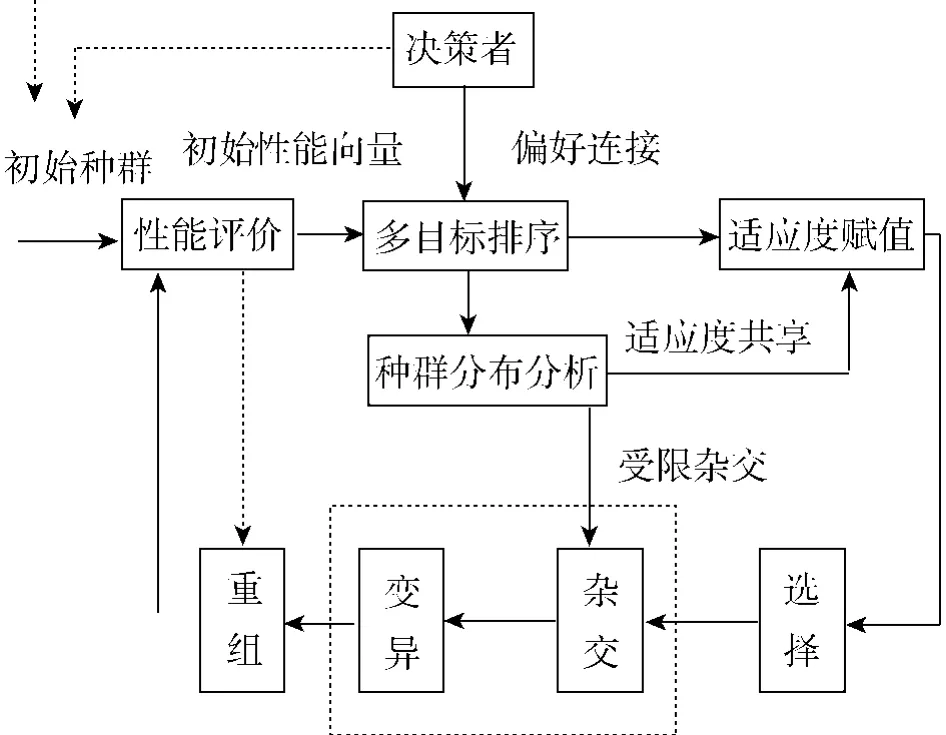
图1 MOGA方法的一般流程Fig.1 General process of MOGA

2 决策技术应用

通过多目标优化算法得到的解实际上是Pareto解的集合，即有不止一个满足方程(1)的解.这些解的特点是至少存在一个目标优于其他所有的解.对于这样一个集合，如果没有关于问题的进一步的信息，很难判断哪个解更加可取，故所有的Pareto解都认为是同样重要的.因此，从这个解集中再挑选出最后的满意解，就需要引入决策技术.对这些Pareto解的选择取决于对它们依据一定的标准进行综合评价，这些方法有很多［10］，例如系统工程方法、模糊数学方法、多属性决策方法等.鉴于每个Pareto解都是具有决策者关注的属性(例如建造费用、投资回收年限等)，本文采用多属性决策的方法进行评价和选优.这类方法具有对评价对象表述比较精确的特点，应用领域广泛.

理想解法亦称为 TOPSIS法［11］(technique for order preference by similarity to ideal solution)，它是多属性决策方法的一种，也是一种有效的多指标优选方法.这种方法通过构造评价问题的理想解和负理想解，即各指标最优解和最劣解，并用靠近理想解和远离负理想解的程度，作为各优选方案的判断依据.假设有m个备选方案，每个方案有n个属性.TOPSIS方法的简要步骤如下:

1)建立标准化的决策矩阵，该矩阵的大小为m×n;

2)引入各属性的权重，对上述矩阵进行加权标准化;

3)确定备选方案中的理想解和负理想解;

4)计算每个方案和理想解、负理想解的n维Euclid距离;

5)计算和理想解的相对接近程度，并按照接近程度的大小排序.

在上述步骤2)中，TOPSIS方法会用到属性的权重.权重是多属性决策技术中一个非常重要的概念.现有评价方法中，指标权重赋权方法大致可以分为2类［12-13］，一类为主观权重，即决策者给出偏好信息，如层次分析法(AHP法)，专家调查法(Delphi)等;另外一类是客观赋权法，即基于决策矩阵获取权重，如信息熵方法、离差最大法、主成分法等.在信息论中，熵值是对于一个系统无序程度的度量，系统的信息被解释为系统无序程度的表达.系统中某项指标所反映的信息表现为系统针对某项指标的变异程度.如果把综合评价所涉及的指标视为一个评价系统，则系统中某项指标的熵值越大，表明它所蕴含的信息量越小，即在系统中相应的变异程度越小，则该指标在综合评价中对应的权重也就越小;反之，某项指标的熵值越小，则它所蕴含的信息量越大，在系统中的变异程度就越大，则该项指标在综合评价中对应的权重也就越大.

本文采用信息熵方法得到决策属性的权值，再利用TOPSIS方法对备选方案进行排序，完成对Pareto解的综合评价，依据此评价得到Pareto解的排序.

3 算例和讨论

对于船舶建造营运类的评价，通常采用价值分析、成本效益分析、价值功能分析等.在国内外船舶工程实践中，经济性指标有多种，它们仅反映了船舶经济性(投资、成本以及利润等)的某个侧面，为了全面衡量经济性，应该避免只选用单一目标.当把经济性论证当成一个多目标优化问题来看待时，就可以把不同侧面的指标当成目标函数来进行分析.为讨论本文提出方法的有效性，这里对一艘内河集装箱船的技术经济论证进行了分析，以3000 t级船型为例［7，14］，通过对航道、船闸、资金等情况的分析确定约束条件，建立起数学模型，并对多个船型进行分析排序.

3.1 优化模型

3.1.1 设计变量

选取船舶垂线间长Lpp、型宽B、吃水T、型深D、方形系数CB和主机型号PeType共6个参数作为设计论证变量.变量的上、下限见表1.变量PeType为1，2，3 分别对应的主机 型 号为 WD618.C-3、WD618.C-2和 WD618.C-1.

表1 设计变量上、下限Table 1 Lower and upper bounds of design variables

3.1.2 约束条件

约束条件包括2类，一类是设计变量间的约束:4.40 ＜ Lpp/B ＜ 5.75，1.77 ＜ B/D ＜ 3.38.(2)另外一类是性能约束，假设造价P＜1500万元.船舶造价P为

3.1.3 目标函数

对内河集装箱船的经济性指标取4个，除了经济性分析通常采用的必要运费率RFR、净现值NPV和投资回收期PBP之外，再增加单位排水量载箱量ATCD作为目标函数.这些目标属性的计算公式为

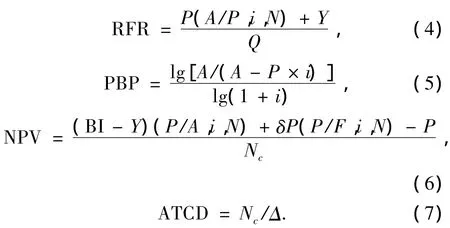
式中:Y为年营运费，元;Q为年运量，t;A为年收益，元;i为贷款利率，%;N为还款年限;Nc为年运箱量;BI为年收入，元;δP为船价残值;Δ为排水量;(A/P，i，N)为资金回收因素;(P/A，i，N)为等额现值因素;(P/F，i，N)为现值因素.营运成本参数见文献［14］.

因此目标函数为

3.2 计算结果和讨论

采用MOGA方法进行寻优的参数设置为:种群数量 500，进化代数5 000，变异率 0.1，交叉率 0.5，选择率0.05.约束函数采用罚函数形式.经过计算，一共得到120个Pareto解，见图2～5.

图2～5给出了4个目标函数之间的散点图.从图中可以看到，这4个目标之间是相互制约的.图2和图4中均表示出了Pareto前沿，这些前沿就是所考虑的2个目标之间最好的解.采用信息熵方法，得到4个目标属性的权重为

可以看出，PBP的权重达到59%，而RFR的权重仅为5%.该权重是基于决策矩阵的客观方法.该权值分布直接影响到方案的排序结果.使用TOPSIS方法，可以得到这120个Pareto解的排序.表2给出了排序前5个的方案，其中排序第1个的方案标识为H.

对于多目标优化问题，为了使各个目标尽可能小，也可以先求出各目标函数的最小值，然后让各目标尽量接近各自的极小值来获得多目标优化问题的解，此即为理想点方法.为此先分别求出上述4个目标函数各自的极小值(结果见表3)，并由这些极小值虚构一个解，即理想解.对于多目标优化问题，这个解一般都是不存在的.这个解用U点标注在图中.从图中可以看出，所有Pareto解都和U点有一定的距离.根据距离U点的远近对这些Pareto解排序，得到最靠近U点的Pareto解为J方案.

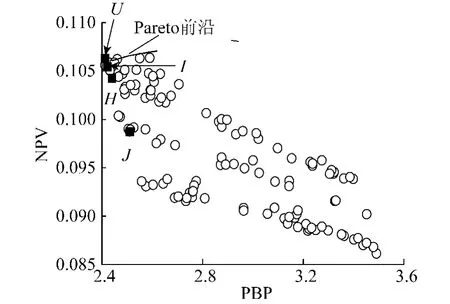
图2 NPV和PBP之间散点图Fig.2 Scatter plot of NPV vs.PBP

图3 RFR和PBP之间散点图Fig.3 Scatter plot of RFR vs.PBP

图4 PBP和ATCD之间散点图Fig.4 Scatter plot of ATCD vs.PBP

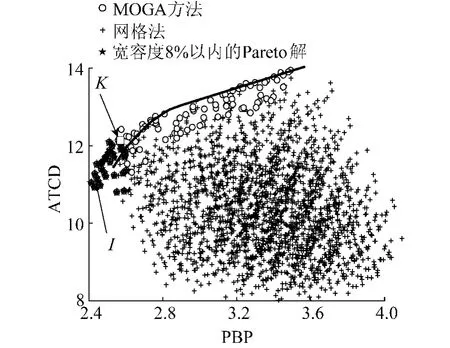
图5 与传统方法的比较Fig.5 Comparison with the traditionalmethods

加权和方法是一种将多目标优化问题转化为单目标优化常用技术.假定另外一组权值向量为

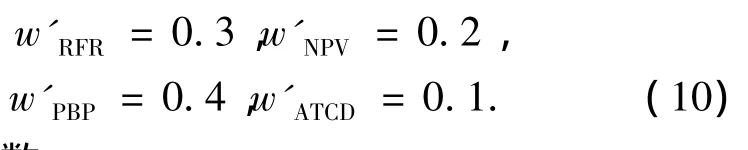
利用目标函数:

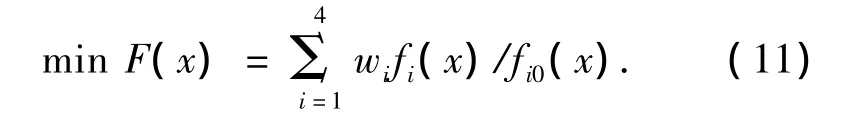
可以得到加权和方法的解.其中，fi0(x)是各个目标函数的极小值.该方法得到的结果用I点表示在图中.显然，不同的权重向量会得到不同的结果.

从图2～4中可以看出，H、J、I这3个方案都是在PBP-ATCD属性的Pareto前沿上(图4)，说明如果从PBP、ATCD属性来考量，这3个方案都是很好的解.但是它们在其他属性上则要稍差一些，例如H、J在图2、3中都距离Pareto前沿有一段距离.这种特性其实正是Pareto解的特点.

宽容度排序也是一种将多目标优化问题转化为单目标优化的方法，它在船型论证中广泛使用［8］.该方法给出目标函数的重要程度，引入目标宽容度的概念，把上一个目标的极小值结合宽容度形成下一个优化目标的约束条件，依次完成单目标优化.假设宽容度为8%，依次对PBP、NPV、RFR和ATCD这4个属性进行优化，得到优化解K点.K方案的PBP、NPV值均比较好，这是由优化的顺序决定的.方案H、I、J、K、U 及单个目标最优的方案具体结果见表3.

借助宽容度的概念，以理想解U点为中心，以各目标值宽容度8%作为半径，在四维空间中对120个Pareto解进行过滤，得到32个解，见图5.这部分的解靠近纵轴，即它们的投资回收年限PBP都比较短，这缘于PBP的权重最大.

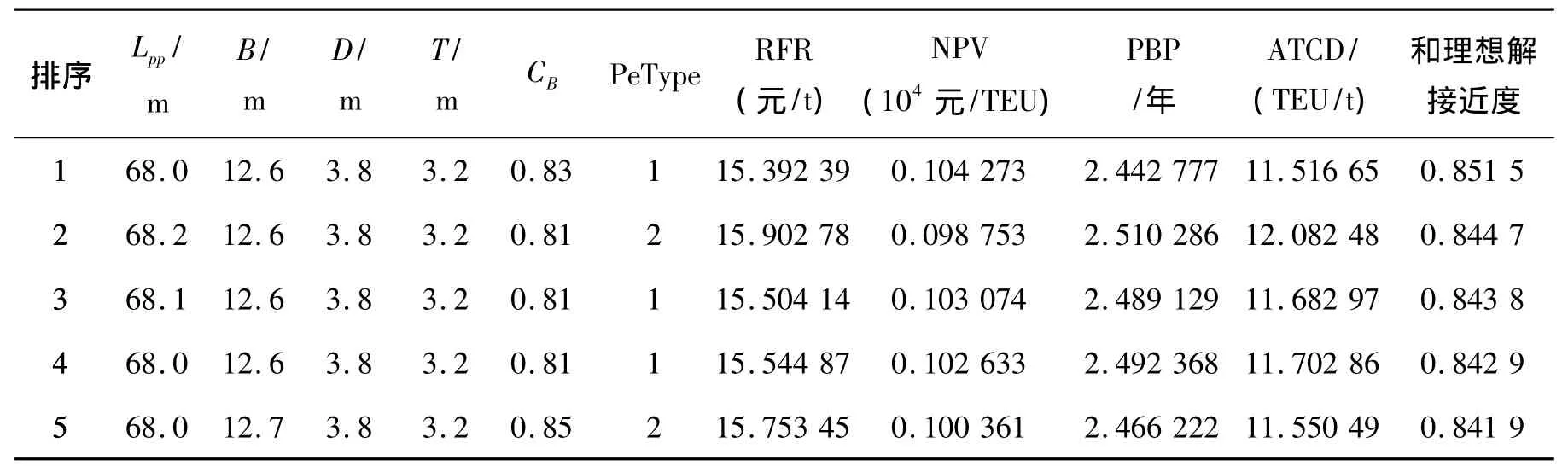
表2 TOPSIS方法排序结果Table 2 Sorted results based on TOPSIS approach

表3 典型方案列表Table 3 List of typical optimization results

船型论证中采用的网格方法，是针对船舶主尺度允许变化范围，按照全组合的方式组成若干船型，这实际上是一种试验设计(DOE)的方法.对上述6个变量进行55×3的全组合，共9375个船型方案.再考虑尺度约束(见式(2))，剔除一部分不合理的解，还余下2 100个解，如图5中网格法的解.图中用实线给出了这些方案的PBP-ATCD属性的外包络线.从图中可以看出，在PBP＞2.8时，外包络线和Pareto前沿吻合程度比较好，但是在PBP＜2.8时，包络线就比Pareto前沿差.DOE方法采用的网格越细，包络线就越逼近Pareto前沿.

由图5可知，从DOE方法得到的船型方案，绝大部分都不是Pareto解.如果把这些解都放到后续的评判和排序中，实际上是不经济的.对那些距离外包络线很远的方案进行排序意义不大.选取这些属性外包络线的所有解进入评估阶段则是恰当的.

4 结束语

将多目标遗传算法和决策方法引入到船型论证研究中，建立了船型论证的两阶段方法和多目标优化模型.文中计算了一个船型论证算例，并且和传统的网格方法、单目标优化方法的结果进行了详细比较，可以看出本文中采用多目标遗传算法可以获取质量较好的船型方案集(即Pareto解集)，采用距离理想解的接近度(TOPSIS)给出了合理的方案排序.本文提出的方法能够有效用于船型论证，能够给出决策者更多的选择，决策结果合理可行.需要指出的是文中在方案排序过程中采用信息熵方法获取权重，这是一种基于决策矩阵的客观方法，实际使用过程中如果对船型论证的各目标函数了解较深还可采用主观方法获取权重，如AHP方法、Delphi方法等.

［1］李树范，纪卓尚，王世连.船舶设计原理［M］.大连:大连理工大学出版社，1988:251-259.

［2］姚雷，李国安，段宏.层次分析法在大型水面舰船船型多方案优选中的应用［J］.中国舰船研究，2006，1(3):12-14.YAO LEI，Li Guoan，DUAN Hong.Analytic hierarchy process applied in large-scale surface warshipmulti-formoptimization［J］.Chinese Journal of ShipResearch，2006，1(3):12-14.

［3］宋庆克，汪希龄，胡铁牛.舰船方案的模糊智能化评价［J］.上海交通大学学报，1997，31(11):51-56.SONG Qingke，WANG Xiling，HU Tieniu.Fuzzy intelligent evaluation on shipschemes［J］.Journal of Shanghai Jiao Tong University，1997，31(11):51-56.

［4］刘寅东，李克秋，唐焕文.数据包络分析模型与方法在船型方案排序择优中的应用［J］.中国造船，1998，39(3):1-6.LIU Yindong，LIKeqiu，TANG Huanwen.Cone ratio data envelopment analysis and evaluation of multi-objective shipplan［J］.Shipbuilding of China，1998，39(3):1-6.

［5］桑松，林焰，纪卓尚.基于神经网络的船型要素数学建模研究［J］.计算机工程，2002，28(9):28-30.SANG Song，LIN Yan，JIZhuoshang.Study ofmathmodeling on ship＇s principal particulars based on neural network［J］.Computer Engineering，2002，28(9):28-30.

［6］柴树红，林焰，迟云鹏，等.金枪鱼钓船船型优化设计及性能试验研究［J］.大连理工大学学报，1998，38(4):484-488.CHAIShuhong，LIN Yan，CHI Yunpeng，et al.Optimization design and investigation of performance test for tuna longtime fishing boat［J］.Journal of Dalian University of Technology，1998，38(4):484-488.

［7］李文龙，谭家华.西江集装箱船主要参数的回归分析与船型优化［J］.造船技术，2002(3):9-13.LIWenlong，TAN Jiahua.The regression analysis and shipformoptimization of the Xijiang container ship＇s principal parameters［J］.Marine Technology，2002(3):9-13.

［8］冯志强，程智斌.非线性规划在船型方案设计中的应用［J］.江苏船舶，2003，20(5):7-9.FENG Zhiqiang，CHENG Zhibin.Nonlinear programming applied in shiptype design［J］.Jiangsu Ship，2003，20(5):7-9.

［9］FONSECA C M，FLEMING pJ.Genetic algorithms for multiobjective optimization:formulation，discussion and generalization［C］//Proceedings of 5th International Conference on Genetic Algorithms.San Mateo，USA，1993:416-423.

［10］陈衍泰，陈国宏，李美娟.综合评价方法分类及研究进展［J］.管理科学学报，2004(2):69-79.CHEN Yantai，CHEN Guohong，LIMeijuan.Classification＆research advancement of comprehensive evaluation methods［J］.Journal of Management Sciences in China，2004(2):69-79.

［11］HWANG C L，YOON K.Multiple attribute decision making-methods and applications:a state-of-art survey［M］.NewYork:Springer-Verlag，1981:69-76.

［12］刘靖旭，谭跃进，蔡怀平.多属性决策中的线性组合赋权方法研究［J］.国防科技大学学报，2005，27(4):121-124.LIU Jingxu，TAN Yuejin，CAIHuaiping.The study of the methods of the linear combination weighting formultiple attribute decision-making［J］.Journalof National University of Defense Technology，2005，27(4):121-124.

［13］徐玖平，吴巍.多属性决策的理论与方法［M］.北京:清华大学出版社，2006:42-48.

［14］刘寅东，余秀丽，苏绍娟.西江干线集装箱船船型论证［J］.船海工程，2011，40(2):9-13.LIU Yandong，YU Xiuli，SU Shaojuan.Technical and economic evaluation for the container ships in Xijiang river［J］.Ship＆ Ocean Engineering，2011，40(2):9-13.