旋转固体火箭变质量运动特性分析①

任天荣，马建敏

(1.复旦大学力学与工程科学系，上海 200433;2.上海机电工程研究所，上海 200233)

0 引言

在固体火箭飞行的主动段，发动机燃料的消耗使火箭自身的质量发生连续改变，此变化对整个箭体运动必然产生影响。对于旋转固体火箭，可视其旋转箭体为一变质量陀螺。而目前对于单通道的旋转固体火箭，在用于状态分析与型号设计的火箭数学模型中，由于“固化原理”的使用，其每个计算阶段均不考虑箭体的变质量特性［1］。因此，关于箭体的变质量特性对箭体的动力学方面的影响，在目前通用的火箭数学模型中是无法体现的。就旋转飞行器而言，固体发动机的变质量作用对飞行器姿态的影响，已有一些从发动机内部非稳态气流、装药方式等角度的研究［2－6］。

本文将从变质量陀螺方程出发，分析旋转固体火箭的变质量特性对箭体旋转角速度的影响，基于微分方程定性理论推证定常飞行的旋转固体火箭有稳定的锥形运动存在，并给出变质量特性对箭体姿态变化的章动阻尼作用的数学解析。

1 旋转固体火箭变质量陀螺运动方程的建立

本文在建立旋转圆柱体变质量陀螺运动方程的过程中，并没有采用文献［7］中的张量概念，同样可建立与之相同的方程。设一圆柱体旋转固体火箭做静稳定飞行，则其速度坐标系近似为惯性坐标系，设原点即为箭体质心;而取箭体的半弹体坐标系为相对转动的动坐标系。将惯性坐标系中动量矩定理的微分过程改在动坐标系内进行，则有

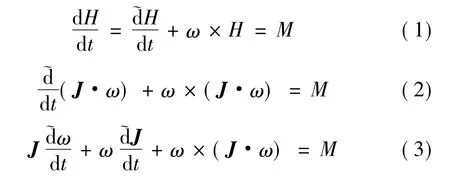
式中 带“～”的微分符号表示动坐标系的局部导数;ω为相对动坐标系的瞬时角速度。

考虑到弹体部分是由弹体和将要离去的燃气质量两部分组成(图1)，假设本文发动机内圆形药柱为端面燃烧，其单位时间发动机内端面烧蚀质量与发动机的质量流量˙m相等。

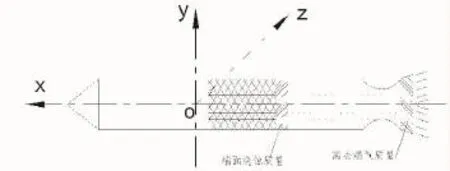
图1 弹体质量分布示意图Fig.1 Mass sketch of a missile

弹体和离去燃气质量相对质心o点的惯性矩阵Jd、Jq分别为

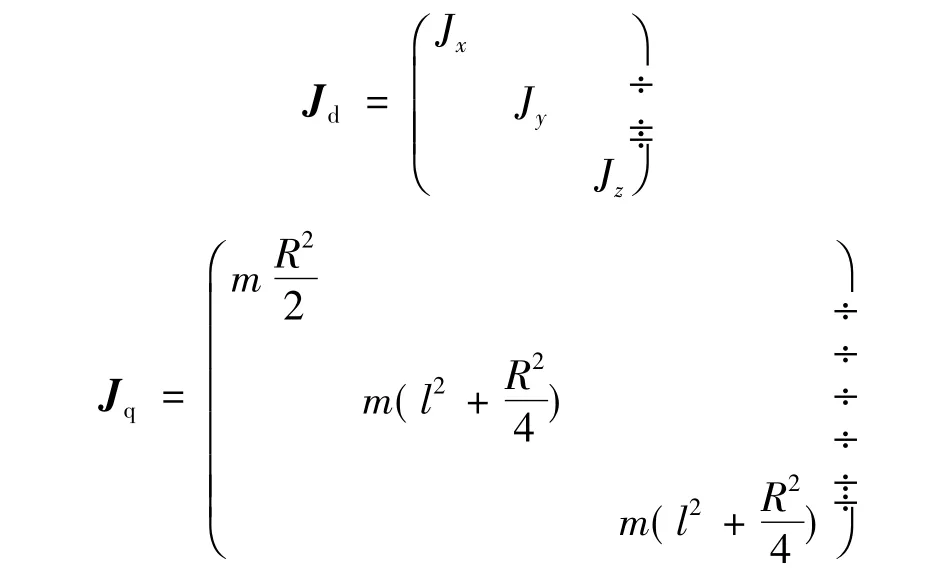
式中 Jx、Jy、yz分别为弹体各轴主惯性矩;为离去燃气质量相对x轴惯性矩;为由平行轴定理知离去燃气质量相对y轴和z轴的惯性矩;l为喷口到质心距离(即离去燃气质量相对弹体质心的距离);R为喷口半径。

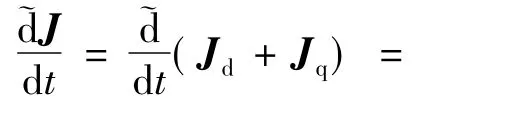
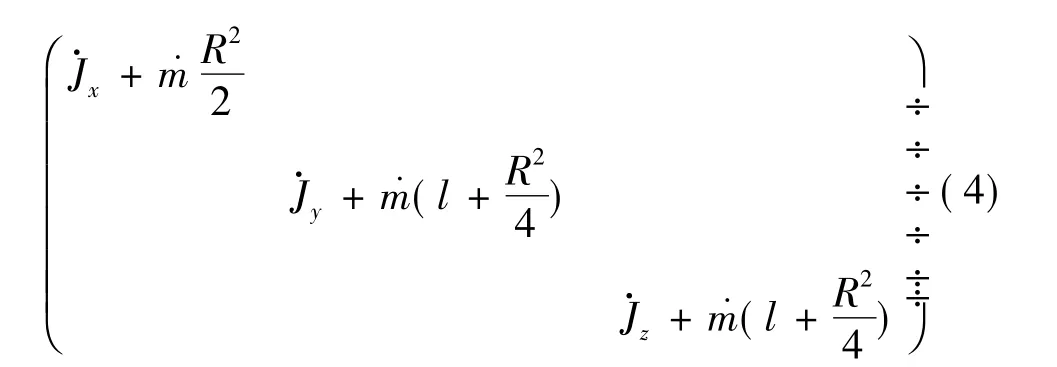
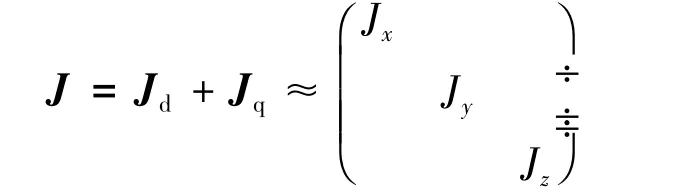
则式(3)为

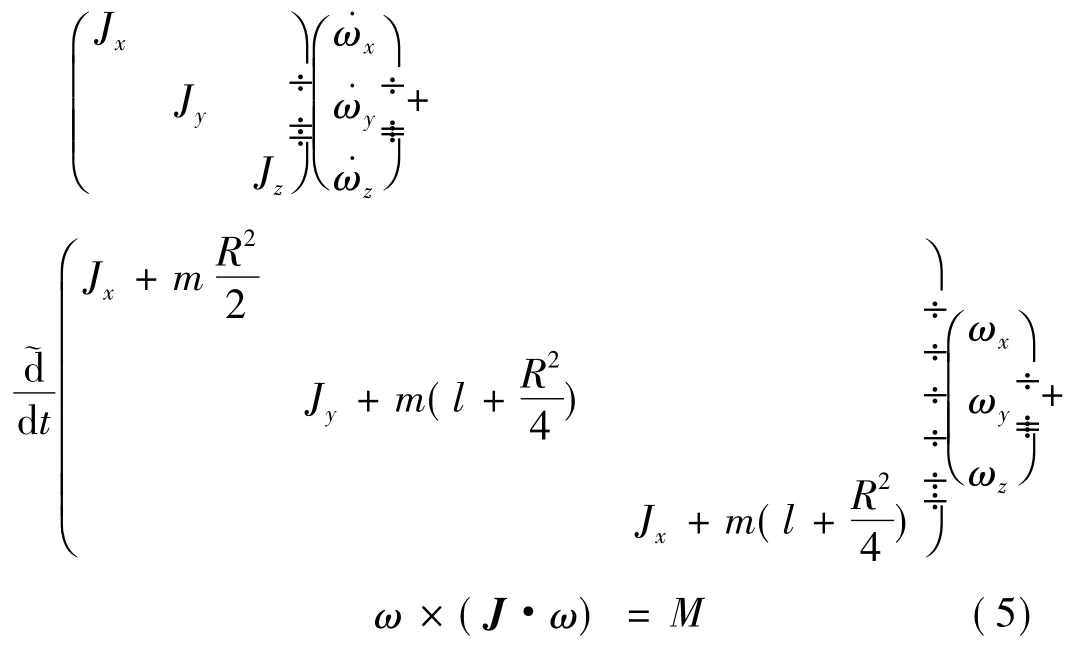
为方便计算，令Jx=J1，Jz=Jy=J。综合之，得端面燃烧旋转固体火箭变质量陀螺运动普遍方程:

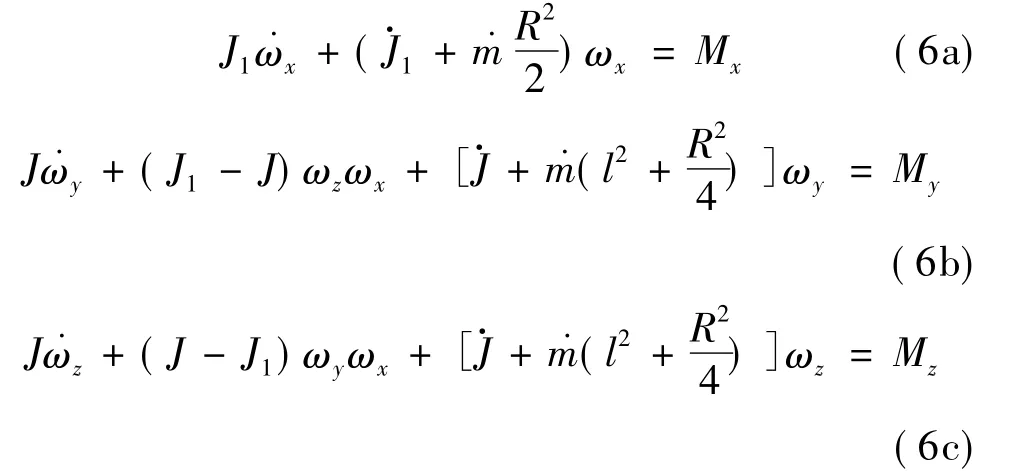
2 变质量特性对自旋转速的影响

旋转固体火箭在飞行试验中，往往会在某时刻发生弹道波动，其原因可以是多种的，但某些双推力固体火箭发动机设计本身就足以导致该现象发生。因主动段发动机燃料不断消耗，可以看成是变质量体，这就造成了箭体角动量矩的改变，并会对箭体的某些运动参数产生一定的影响。假设，轴向干扰力矩Mx=0，发动机稳定燃烧使箭体轴向转动惯量线性变化J1=Jx0+，式中Jx0为初值。由式(6a)推导出:

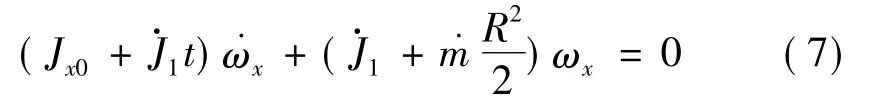
则由式(7)求得

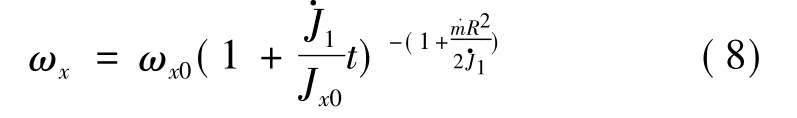
其中，ωx0为前一时刻的箭体自转速度，由于总有˙J1≤0，再由前面知˙m≥0。故为使ωx不变，需要˙J=0，此仅在发动机不工作状态方可行;或者使，即

假设因燃烧减少的圆柱状发动机内燃气质量是均匀的，则箭体轴向转动惯量的增量，则有将其代入式(9)则有

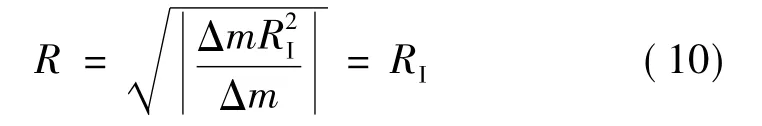
式中 RI为燃烧室内径。

式(10)表明，当发动机燃烧室内径与尾喷管直径相等时，发动机质量流量对弹体自旋转速度没有影响。

国内多个型号的旋转固体火箭在助推段向巡航段过渡时，均有转速波动进而引发弹道波动的现象发生，即所谓的“3 s跳”问题，这与采用收缩尾段，使尾喷管口直径较燃烧室内径小有直接关系。

从机理上分析，若发动机喷管口径很小，则燃烧室内径相对较大，被喷出的燃气流自旋角动量就小，即带走的动量矩也就少于此部分燃气在燃烧室内原有的动量矩。但是动量矩是守恒的，则箭体的动量矩就会增加，则箭体自转速度就必然上升;同理，若喷管口较粗，燃气流带走的自旋角动量较多，即动量矩带走较多，则箭体自旋角速度的增加必然减小。再由圆柱旋转体的Kutta-Joukowski升力公式可得

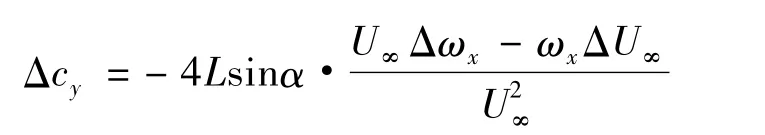
式中 α为攻角;L为箭体长度;U∞为来流速度。

3 锥形运动的存在性

在旋转飞行器的风洞试验和飞行试验中，虽不每次但却时常出现的锥形运动已有许多研究［8－13］，但这些研究均是在默认锥形运动已有的前提下进行的，并没有从理论上对锥形运动的存在性给出明确的说明。下面利用微分方程定性理论中的Bendixson-Dulac定理［14］，对变质量陀螺运动普遍方程的极限环运动的存在性进行探讨，来分析在线性阻尼条件下旋转固体火箭锥形运动的存在性。

由Bendixson-Dulac定理，给定微分方程组:

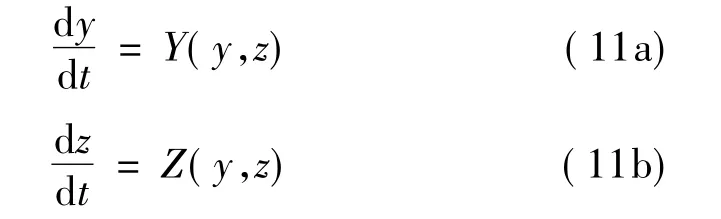
其中，Y、Z∈C1(D)，D是环域，D中无奇点。

若存在函数 B(y，z)、M(y，z)∈C1(D)，B(y，z)＞0且在环域D上有

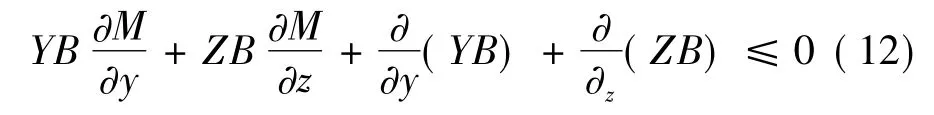
而等号不能在整条轨线上成立，则在D上至多有一个极限环。若此极限环存在，则是稳定的。

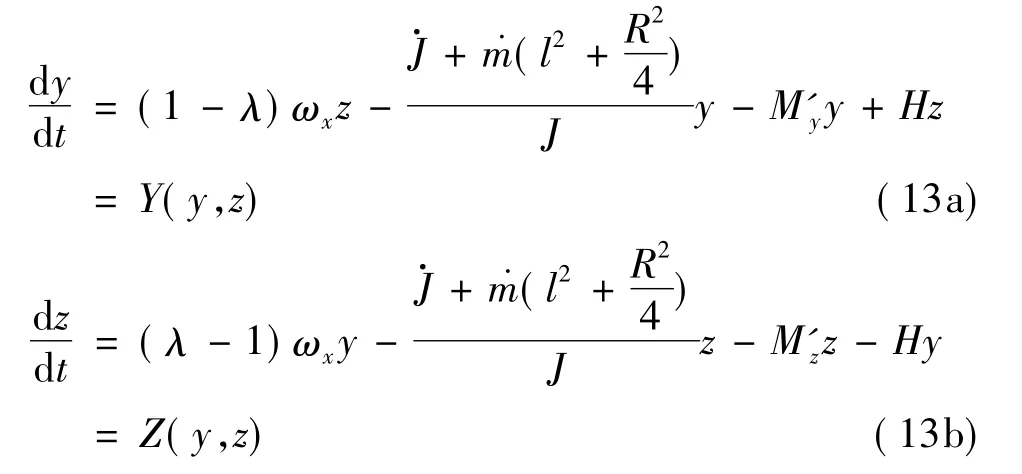
再令 B(y，z)=z2，另设 M(y，z)= －2lnz，则再取充分小的δ＞0及充分大的Σ＞0，则有环域显然在环域D上，有 Y(y，z)、Z(y，z)、B(y，z)、M(y，z)∈C1(D)，且 B(y，z)＞0。再分别计算易得

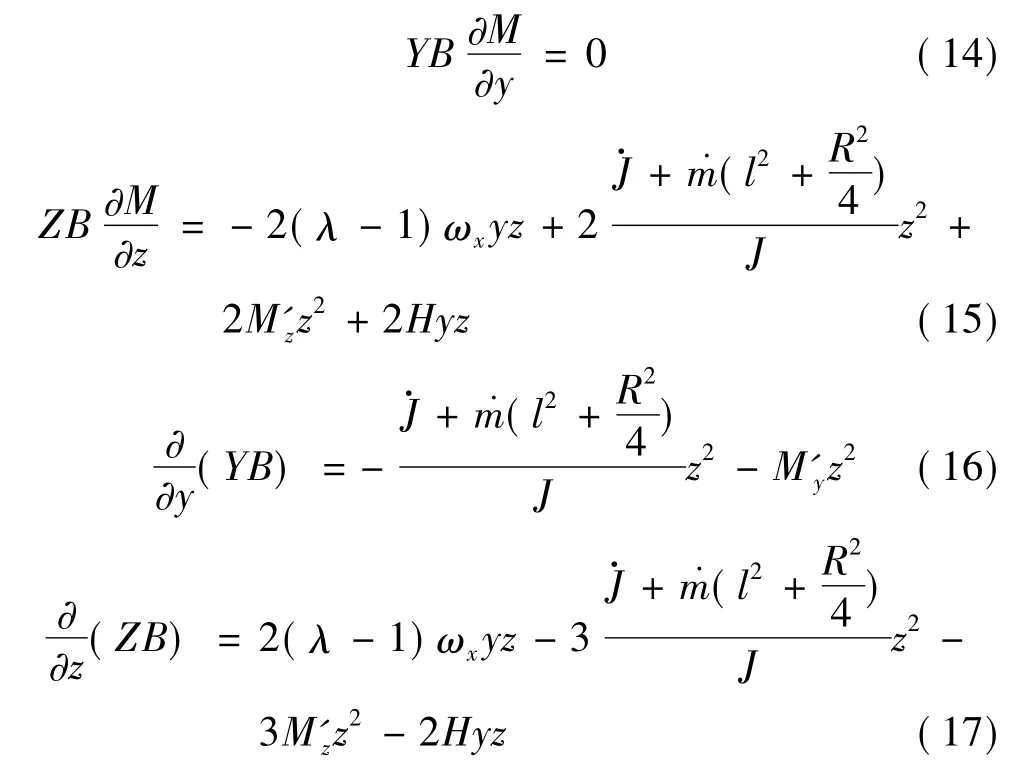
则

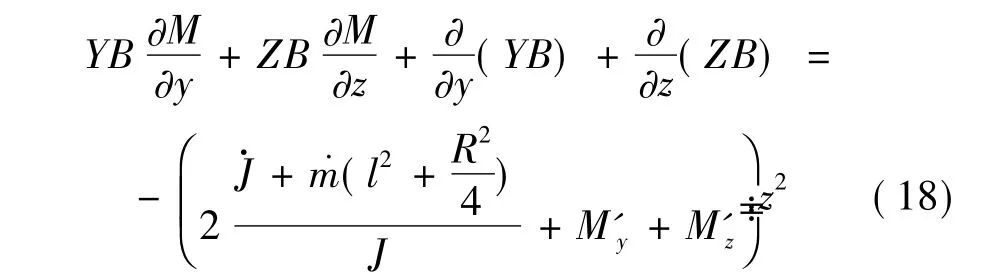
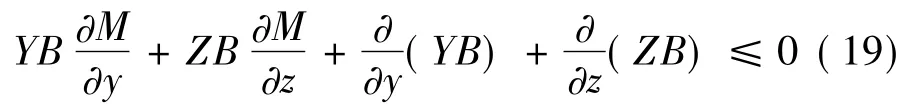
显然式(19)等号不会在环域D上的任意一整条轨线上成立;所以方程组(13a)、(13b)满足Bendixson-Dulac定理条件，故有如下结论:在线性阻尼力矩条件下，主动段飞行静稳定的旋转导弹，其横向角速度矢量幅值要么为零，要么矢量端点趋于一个稳定的极限环运动。下面分几种情况讨论:

(1)当静稳定的旋转箭弹自旋转速不变时，其横向角速度矢量幅值要么为零，则此时箭体不发生锥形运动;要么横向角速度矢量端点处于一个稳定的极限环运动，则箭体表现为且仅表现为一种稳定的锥形运动。

(2)在上述的整个分析过程中，并没有涉及到ωx=0和Mx在弹轴方向的影响，所以对于非旋转火箭，在一定的条件下也同样会发生锥形运动，如飞船返回舱。当飞行器不受持续的外力矩作用，即Mx=0，My=0，Mz=0时，也可以存在锥形运动。

(3)对于旋转固体火箭，无论其是否处于气动静稳定或中立稳定状态，均可存在稳定的锥形运动。

(4)箭体滚转方向阻尼的存在会减小箭体沿x方向的自旋转速，而稳定极限环的存在使横向角速度矢量幅值保持稳定，则箭体总的合成角速度将与x轴夹角变大，进而使箭体锥形摆动的幅度加大，所以箭体滚转方向阻尼不利于锥形运动的控制;在主动段由于有发动机可维持箭体转速的稳定，则横向阻尼的不利影响会被抵消;但在被动段飞行时，横向阻尼会对箭体姿态的不利影响加大。

4 旋转固体火箭变质量特性的章动阻尼作用

主动段飞行的旋转固体火箭受到气动力、重力和发动机推力的共同作用。当飞行中的箭体受到横向扰动，即章动方向扰动，箭体会产生附加的角运动，就同时会出现3种始终与角运动方向相反的阻尼力矩:附加空气动力产生的气动阻尼力矩;发动机工作时燃烧室内部存在轴向质量移动而产生的哥氏阻尼力矩;发动机尾喷流的离去燃气质量产生附加的哥氏章动阻尼力矩。在绝大部分的型号设计中，往往仅考虑气动阻尼力矩，而后2种阻尼力矩往往忽略不计。下面给出变质量特性对箭体的章动阻尼作用的解析公式。

由前面分析知，在箭体上没有外力矩作用时，也可以存在锥形运动。故首先设Mx=0，My=0，Mz=0，再引入复变量 u= ωy+iωz，μ = μy+iμz，则可将式(6b)、(6c)化为

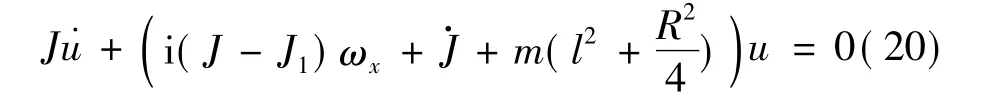
求解方程(20)得

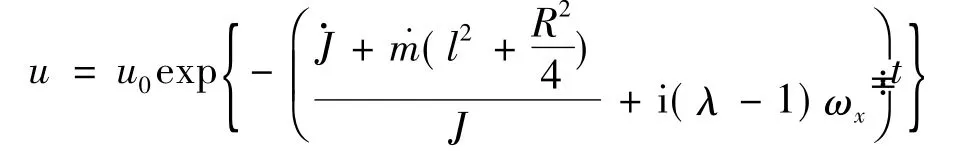
故有

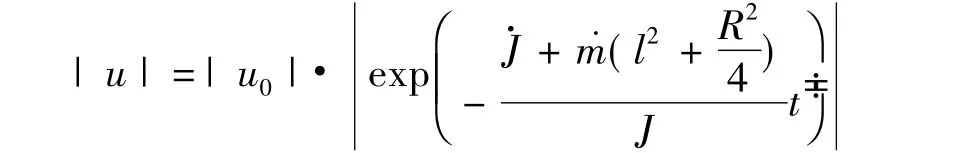
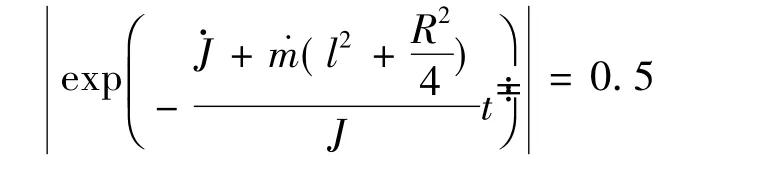
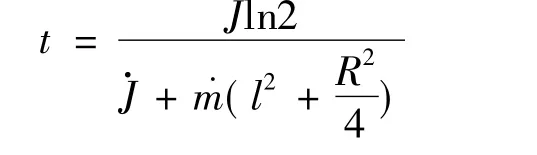
将上面变量数值代入，得半衰期为1.34 s。

在国内型号研制的飞行试验中，均发现实测的弹箭主动段振荡频率，总是小于仅考虑气动阻尼项的理论计算频率的现象。这是实际飞行中，由于燃气喷流阻尼作用存在，再加气动阻尼，使得弹箭体真实的阻尼系数较理论计算时所用阻尼系数大，故而实测的弹箭振荡频率在主动段总是小于理论结果。所以，尾喷流的阻尼作用是不应忽视的。

5 结论

(1)对药柱端面燃烧的双推力旋转固体火箭发动机，当尾喷口半径与发动机燃烧室半径一致时，能减弱其在助推段向巡航段过度过程中，所产生弹道波动现象，即所谓的“3 s跳”问题。

(2)在箭体自旋转速不变时，主动段飞行的旋转固体火箭，要么不发生锥形运动，要么仅发生一种稳定的锥形运动。

(3)在自旋转速保持稳定时，旋转弹箭飞行中横向阻尼的存在，不会影响弹箭锥形运动的幅度;但在被动段飞行时，滚转方向的阻尼会使弹箭绕自身纵轴旋转速度下降，致使弹箭锥形运动的幅度加大，从而对姿态稳定造成不利影响。

(4)主动段飞行的旋转固体火箭，其发动机尾喷流对弹箭的摆动起章动阻尼作用，质量流量越大，尾喷口半径越大，喷口到质心距离越大，其阻尼作用越大。该阻尼使实际飞行中的弹箭振荡频率，比仅考虑气动阻尼的理论频率小。

［1］钱杏芳，林瑞雄，赵亚男.导弹飞行力学［M］.北京:北京理工大学出版社，2000.

［2］Mao T C，Eke F O.Attitude dynamics of a torque－free variable mass cylindrical body［J］.The Journal Astronautical Sciences，2000，48(4):435-448.

［3］Eke F O，Mao T C，Morris M J.Free Attitude motion of a spinning body with substantial mass loss［J］.The Journal of Applied Mechanics，2004，71(3):190-194.

［4］Yam Y，Mingori D L，Halsmer D M.Stability of a spinning axisymmetric rocket with dissipative internal mass motion［J］.Journal of Guidance Control and Dynamics，1997，20(2):306-312.

［5］郜冶，刘平安，杨丹.旋转飞行器固体火箭发动机非稳态气流作用分析［J］.宇航学报，2010，31(6):1637-1644.

［6］杨丹，郜冶，熊永亮.旋转固体火箭发动机随质量变化的姿态运动分析［J］.推进技术，2008，29(1):8-12.

［7］Cornelisse J W，Schoyer H F R，Wakker K F.火箭推进与航天动力学［M］.杨炳尉，冯振兴，译.北京:宇航出版社，1986:84-97.

［8］Morote J，Liano G.stability analysis and flight trials of a clipped wrap around fin configuration［R］.AIAA 2004-5055.

［9］Mao Xue-rui，Yang Shu-xing，Xu Yong.Research on the Coning motion of Wrap-around-fin Prejectiles［J］.Canadian Aeronautics and Space Journal，2006，52(3):119-125.

［10］王华毕，吴甲生.火箭弹锥形运动稳定性分析［J］.兵工学报，2008，29(5):562-566.

［11］赵良玉，杨树兴.卷弧翼火箭弹圆锥运动收敛速度计算方法［J］.固体火箭技术，2009，32(1):15-19.

［12］闫晓勇，杨树兴，张成.基于章动理论的火箭弹锥形运动稳定性分析［J］.兵工学报，2009，30(10):1291-1296.

［13］任天荣，马建敏.基于陀螺力学的旋转导弹锥形运动分析［J］.宇航学报，2010，31(9):2082-2087.

［14］张芷芳，丁同仁，等.微分方程定性理论［M］.北京:科学出版社，1985:230-275.