主从轴运动控制中5次方曲线的设计

刘泽洋

（上海交通大学自动化系，上海 200240）

现在一般伺服运动中，如果是控制电机走固定位置的方式，上位控制系统PLC 一般都是让伺服走一个梯形的位置块。这种模式都是单轴的运动模式，在这种情况下，每个轴的运动都是独立的，而不是关联的。在这类运动方式下，如果要将2个轴或者多个轴的运动建立联系，只能通过上位PLC 将2个轴或多个轴进行逻辑关联。

例如在某个时间节点，PLC 通过逻辑判断要某2个轴一起运动，则发出一个触发信号，触发2个轴开始运行先前设定好的速度指令或者位置指令。但是在这个模式下，一旦PLC 发出触发指令后，2个轴就开始各自进行运动，在完成当前运动前，PLC 是无法进行过程干预，或者2个轴之间是无法进行速度或者位置关联的。所以，这类模式是无法保证过程中的2个轴的关联性。

如果在运行的过程中，任意一个轴的速度有变化，或者位置有波动，其他轴是无法获知这个情况，还是会根据之前的设定继续完成该步骤。

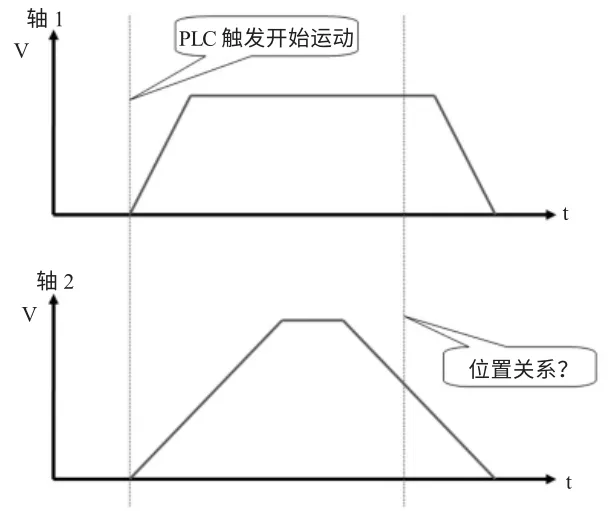
图1 PLC 控制的2 轴运动方式图

所以为了解决这个问题，市场上出现了运动控制器。运动控制器集成了原先PLC 的所有功能，同时增加了多轴的同步运动控制。

多轴的同步运动控制，就是将原先PLC 的轴和轴之前的逻辑关系，转变成了一一对应的位置关系。

图2 走位置同步的从轴块位移和速度曲线图

图2 显示的就是一条同步运动中从轴相对于主轴的位置曲线。红色的是位置曲线，蓝色的是速度曲线。用户先在程序中完成想要实现的曲线动作，然后下载到运动控制器中，运动控制器在程序运行的过程中，根据这条曲线来判断主轴和从轴的位置关系，并实时地根据主轴反馈回来的位置信号，发送对应的位置命令给从轴，从而实现了轴和轴之间的位置同步功能。

这个功能在市场上一部分运动控制器中都能够实现。但并不是说，使用了这个功能做出来的设备的效果，就一定非常好，非常完美了。

从图2 中可以发现，在伺服电机从位置零走到100%完成点的过程中，位移曲线实际上是一条由3段曲线拼接而成的。第一段是一条加速曲线，中间是段匀速区间，最后一段是条匀减速曲线。

相对应的，速度曲线也是由3 段曲线拼接完成，第一段是斜率恒定的匀加速曲线，所以速度是从0开始加速上升的；中间段是匀速过程，所以速度值是一个恒定的值；最后一段是匀减速，所以速度从匀速值开始减速下来到0。

这条曲线初看起来好像挺不错的，位移曲线比较圆滑，速度是匀加速的，也没有跳变。但是再进一步分析之后，就会发现有问题存在。

图3 走梯形位置块速度和加速度曲线图

图3 中绿色的线是加速度曲线，可以发现加速度曲线也是分成3 段的，而速度曲线的加速和减速，实际上是因为加速度曲线的改变。在速度曲线的匀加速段，加速度曲线有一个恒定的正向输出值，从0时刻开始存在，一直到匀加速段结束。在匀速运动段，加速度为零。在匀减速段中，加速度值从0 变为负值，是伺服电机的速度从匀速开始逐步减速到0。

这个时候问题就出现了，虽然位移和速度都是逐步变化，没有跳变，但是对于加速度来说，则是一个跳变的过程。因为从零位开始，加速度是从0 直接跳变到一个恒定值，中间没有递变过程；然后在要达到匀速运动的时候，又是一个加速度跳变，从恒定值直接跳变回0；在匀减速运动开始的时候，又从0 直接跳变成一个负值；最后在运动结束的时候，再次从负值直接跳变成0。

这样问题就出来了：对于伺服系统来说，加速度对应伺服电机的扭矩，加速度的变化对应的实际上就是电机扭矩的变化。如果伺服系统的加速度跳变的话，对应的伺服电机的扭矩就会跳变。上图显示的一个完整的运动过程中，一共有4 次加速度跳变，所以对于伺服电机来说，一个运动周期就会有4 次扭矩跳变。虽然扭矩的变化对于伺服电机来说比较正常，但是如果伺服系统带的负载是一个比较大的设备，扭矩输出很大；或者负载端是比较精密的设备，不允许有任何跳变引起的振动；又或者产品刚性比较差，不允许有扭矩的突变的话，这个时候，问题就比较麻烦了。

这样回到最初的问题，因为现在的伺服系统基本都是采用这种运动方式来走定位，如果不能采用梯形位置块模式，那还能采用什么模式呢？

通过查阅相关资料，加上一些研究，发现有一种类型的曲线，可以不受加速度跳变的限制，并且可以自由设定加速度值，甚至可以设定加速度的加速度，即加加速度。这种曲线就是5 次方曲线。

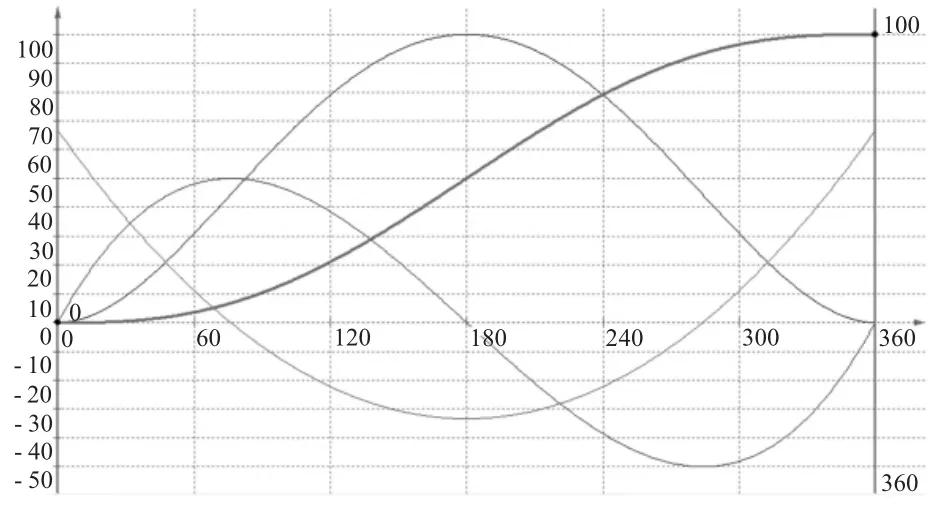
图4 5 次方曲线图

图4 显示的是一条标准的5 次方曲线，红色的是位移曲线，蓝色的是速度曲线，绿色的是加速度曲线，紫色的是加加速度曲线。可以发现，和普通曲线相比，多了一条加加速度曲线，也正式因为有了这条加加速度曲线，加速度曲线才能不用跳变。

如果将5 次方曲线应用在之前的梯形位移曲线上，效果会如何？

图5 应用5 次方曲线后的梯形位置块

可以很明显的发现，在应用了5 次方曲线之后，速度曲线、加速度曲线，都比之前的曲线更平滑柔顺，没有任何的阶跃和跳变了。速度曲线和之前一样，是从0 开始增加，一直增加到匀速段，之后匀速运行到减速段，在逐步减速到0。

而加速度曲线则和之前的完全不同：之前的曲线，加速度是从0 直接跳变的，之后保持恒定值，直到匀速段后再突然跳变回0。而现在5 次方曲线中，加速度是从0 开始有弧度的增加，在达到拐点后再有弧度的减少，当曲线要达到匀速运行段的时候，加速度正好回复到0。这中间没有一点阶跃或者跳变，都是平滑的运动。减速段也是一样，平滑地减速到0。

所以在用了5 次方曲线之后，就不用担心因为扭矩阶跃跳变而引起的负载突然变化，精度变差甚至损坏产品的问题发生了。

那么5 次方曲线到底是个什么曲线？为什么叫做5 次方曲线？曲线的方程式是什么？它又是如何影响曲线的速度，加速度和加加速度的呢？

5 次方曲线之所以叫做5 次方曲线，是因为在其位移方程式中，对于自变量X 最高有5 次方指数来影响方程式结果的。5 次方的方程式具体结构如下：

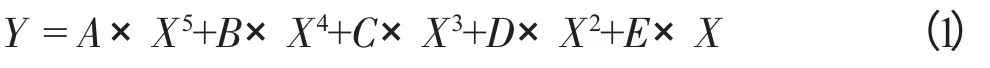
式中A、B、C、D、E 都是系数，而X 代表的是时间，或者是主轴的位置；而Y 代表的是从轴（或者说是该伺服电机本身）的位置。

5 次方曲线按照上面方程式求出来的结果是位置值，也就是位移曲线；如果要求速度曲线，就必须将该方程式求导，也就是将位移对时间求导，得出速度曲线。所以5 次方曲线的速度曲线方程式是：

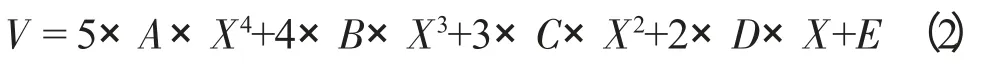
同样的，加速度曲线的方程就是对速度曲线方程再求一次导：

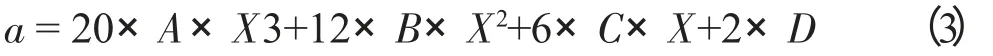
而加加速度的方程就是对加速度方程求导：

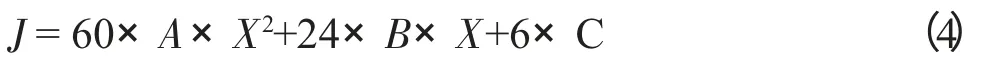
现在方程式有了，但是方程式的系数ABCDE 都没有确定，还是无法求出具体数值的。所以需要将特殊的点带入方程式中，来求出系数ABCDE。

通常选取的特殊点是曲线的起始点和终点。比如起始点的起始位置是0，对应的从轴位置也是0，起始速度是0，加速度是0，则对应的求解方程就有：

根据这3个方程式，可以得出D 和E 的值是0。

但是知道这2个系数还不够，还需要知道ABC的值才能最终确定方程式。所以我们需要终点的数据：终点X 位置值1（100%），从轴位置1（100%），速度为0，加速度0。

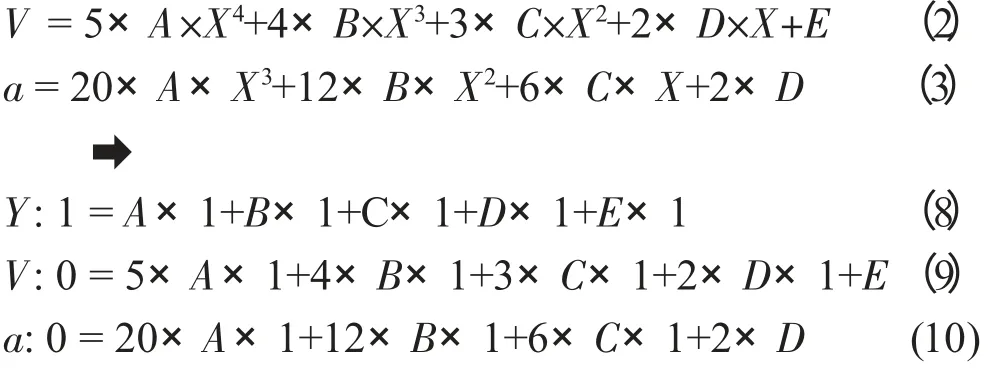
同时带入之前求得的D 和E，求出ABC 的值分别为：

A =6,B=-15,C=10。

所以按照之前给的设定条件，初始点和终点的具体值：

初始点：主轴位 置0，从轴位置0，起始速度0，起始加速度0；

终点：主轴位置1，从轴位置1，终点速度0，终点加速度0；

得到的5 次方曲线为：

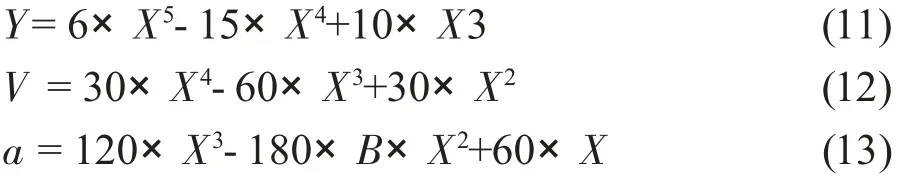
这个就是条标准5 次方曲线的方程了，如果按照方程式画出曲线来的样子就如下：

图6 5 次方曲线位置，速度，加速度和加加速度图

但是有一点要确定的是，每条5 次方曲线都会因为初始条件的不同（起始点和终点的位置，速度，加速度），而是每条曲线的ABCDE 都不一样。所以，只要前提条件变化了，就必须重新计算方程式，不然曲线就不是一样平滑的5 次方曲线了。