简化UKF在机载IRST系统被动测距中的应用

冯国强， 李战武， 柳 毅

(1.空军工程大学工程学院，西安 710038; 2.光电控制技术重点实验室，河南洛阳 471009)

0 引言

机载红外搜索跟踪(Infrared Search and Track，IRST)系统是一类重要的无源探测系统，通过热点跟踪方式对目标进行探测跟踪，与机载雷达系统相比，具有隐蔽性好、抗干扰能力强等优点。通常，机载IRST系统仅能提供目标的方位角及俯仰角信息，但无法提供目标的距离信息，也就无法真正地实现无源定位。这样，如何实现机载IRST系统被动测距的研究课题就被提了出来［1］。

被动测距是讨论如何利用角度观测值估算距离的问题。其主要思想是采用滤波算法从获得的目标角度信息中实时准确地估计目标的距离信息。为了满足实际工程需要，提高距离估计精度和实时性，设计合适的滤波算法是被动测距的关键［2－3］。由于缺乏距离信息，直角坐标系下机载IRST系统观测方程的非线性性质决定了被动测距必须采用非线性滤波方法。传统的非线性滤波方法是扩展卡尔曼滤波(Extended Kalman Filer，EKF)［4］，但在扩展卡尔曼滤波方法中，由于对非线性函数的一阶线性化，使得解析的状态分布在此过程中不可避免地引入了线性化误差，降低了滤波精度甚至导致滤波器不稳定。为了改善对非线性问题的滤波效果，Julier等人提出了无迹卡尔曼滤波(Unscented Kalman Filtering，UKF)方法［5］，它是对非线性系统的概率密度函数进行近似，而不是对系统非线性函数进行近似，因此避免引入线性化误差，且不需要计算Jacobi矩阵，比EKF算法具有更好的稳定性及跟踪精度。但标准UKF算法，不仅需要对状态空间进行扩维，而且不论系统的状态方程和测量方程是否为非线性方程，需要同时进行无迹变换，运算量大。如将其应用到机载IRST系统被动测距中将严重影响目标距离估计的实时性，这对于瞬息万变的空战态势来说十分不利。

针对上述问题，本文根据机载IRST系统被动测距的数学模型，在不影响滤波性能前提下，对标准UKF算法进行简化，给出了一种简化的UKF(SUKF)算法。该算法无需对状态变量扩维，也不需要用Sigma采样点来近似状态预测值和方差，在保持UKF滤波性能的同时又降低了计算复杂度，有利于实际应用。仿真实验验证了SUKF在机载IRST系统被动测距中的有效性。

1 标准UKF算法

标准UKF适用于任何非线性系统的状态估计，算法如下。

设离散系统的状态方程为

观测方程为

式中:Xk为n维状态向量;Zk为m维观测向量;wk－1为与状态无关的p维状态噪声，协方差为Q;vk为独立于状态噪声的q维观测噪声，协方差为R。

从式(1)、式(2)可以看出，状态噪声和观测噪声均为非线性方程的变量，对应着标准UKF。在求Sigma点时，需要对状态进行扩维处理［6］，针对式(1)定义的系统，令

1)初始化。

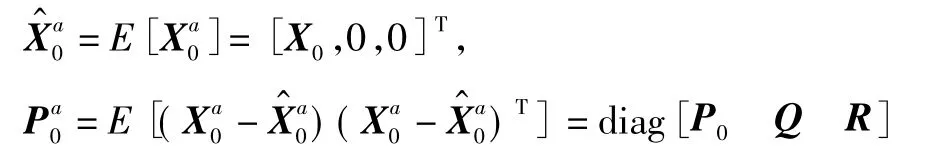
2) 计算 Sigma点及其相应的权值［7－8］。

采用比例修正对称采样产生扩维状态的Sigma点集式中:λ=α2(N+κ)－N 为比例因子，1e－4≤α≤1用来控制无迹变换Sigma样本点的分布范围，当系统非线性较强时，给α取一较小正值，κ为自然数，β≥0主要用来控制后验分布函数高阶矩的影响，在高斯分布情况下，选取为矩阵均方根的第i行或第i列，该矩阵均方根的求解可由Cholesky分解得到。

3) 时间更新［8］。

4) 测量更新［8］。

由于N=n+p+q，易知扩维后的采样点数为2N+1，算法复杂度为0(N3)。显然，标准UKF算法的复杂度与扩维状态的维数成三次方递增，当n、p和q的维数都较高时，运算量显著增加，这对实时应用场合是不利的。

2 机载IRST系统被动测距数学模型

载机地理坐标系中目标相对于观测载机的空间几何关系如图1所示。

图1 直角坐标系中目标－载机相对几何关系Fig.1 Relative geometrical relation between the airplane and target in rectangular coordinates

机载IRST系统被动测距问题可描述为:已知观测时间序列上载机的位置坐标{(xo1，yo1，zo1)，(xo2，yo2，zo2)，…，(xok，yok，zok)}，利用 IRST 系统测量的目标方位角和俯仰角{(β1，ε1)，(β2，ε2)，…，(βk，εk)}，计算目标相对距离{r1，r2，…，rk}。

2.1 系统状态方程

如图1所示，取目标相对运动状态变量为Xk=，而其增加下标“O”与“T”分别表示载机和目标在地面三维直角坐标系中的状态变量，考虑到测角被动测距的可观测性［9－10］，设载机在三维空间里机动运动，第k时刻的加速度为Uok=［aox，k，aoy，k，aoz，k］T，载机的状态方程为

设目标匀速直线运动，状态方程为

其中状态噪声 wk－1=［wx，k－1，wy，k－1，wz，k－1］T是相互独立的零均值高斯白噪声，其协方差为:Qk=Q=qI3×3。

则在载机地理坐标系中，匀速运动目标的相对状态方程为

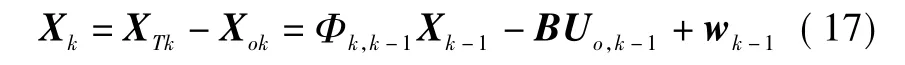
2.2 系统观测方程

根据模型中的几何关系，方位角βk、俯仰角εk和待估计量(xk，yk，zk)关系为

用状态方程法表示观测方程为

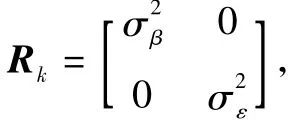
3 SUKF在机载IRST系统被动测距中的应用

3.1 SUKF算法的基本思想

在很多实际应用场合，系统的模型并不像式(1)那样复杂，一般会存在以下两种情况［11］:1)状态噪声wk－1和/或观测噪声vk为加性噪声;2)状态方程和测量方程并不都是非线性方程。当实际系统满足以上条件之一时，均可考虑在保证滤波器性能的前提下对标准UKF进行适当的简化，以达到降低计算量的目的:简化算法中，对于加性噪声，无需对状态量进行扩维，可以不同程度的减少运算量;而对于线性方程，理论上由于卡尔曼滤波器(KF)是最优的，因此可以直接用KF进行运算，而不必用多个采样点来近似，这就是简化的UKF(Simplified UKF，SUKF)算法思想。

3.2 机载IRST系统被动测距中的SUKF算法推导

考虑式(16)和式(19)所描述的机载IRST系统被动测距模型，观测方程是非线性的，而状态方程是线性的，且状态噪声和观测噪声都是加性的高斯白噪声。由前面的讨论知，用SUKF算法进行处理时，无需对状态变量进行扩维，同时对于线性状态方程直接应用KF进行时间更新，由此得到的SUKF算法的详细流程如下。

2)时间更新。

3)测量更新。

计算Sigma采样点

式中:L是状态维数。

4 仿真分析

下面对本文所提算法进行仿真验证，并与EKF、UKF进行对比。

4.1 仿真设计

目标从位置(32 km，29 km，5 km)开始，沿X轴正方向匀速直线运动，速度大小为0.25 km/s。为满足可观测性要求，观测载机从位置(10 km，10 km，3 km)开始，以0.25 km/s速度沿平行于目标的运动方向反复循环作加速—减速—加速运动，加速度为±0.5g，速度变化范围为［0.25 km/s 0.4 km/s］。其中t时刻加速度的变化满足如下规律

载机利用IRST系统测量的角度信息完成目标距离的估算。测量误差分两组，第1组误差较小，方位角、俯仰角测量误差为0.5 mrad;第2组误差较大，方位角、俯仰角测量误差为2 mrad。

仿真中滤波器初值分两种情况设置:1)初值有误差，假定目标距离搜索范围为0～150 km，速度范围假定为 －0.45～ +0.45 km/s，在此假定下可由概率论知识得到目标位置和速度的期望值以及协方差值作为滤波器初始条件［12］;2)初值准确，无误差。

仿真性能用测距误差衡量，定义第i次仿真中k时刻的测距误差为

其中:N为观测次数;M为Monte-Carlo仿真次数，仿真中采用M次仿真实验距离误差的平均值作为测距误差的输出。

设采样周期T=1 s，观测次数N=200 s，在相同的初始条件下进行100次Monte-Carlo仿真。实验是在一台Pentium 4 CPU 3.06 GHz计算机上利用Matlab完成的。

4.2 仿真结果及分析

图2给出了初值有误差情况下，不同测量误差的距离误差曲线。由图2可以看出，对于第1组误差较小的情况，SUKF和UKF都可以在90 s内将测距误差收敛至100 m以下，并且随着时间推移，二者测距误差曲线几乎完全重合，而EKF收敛效果最差，表现为收敛速度慢、测距精度不高;对于第2组误差较大的情况，各算法的距离估计误差都有所增加，SUKF和UKF的收敛效果仍优于EKF。尽管SUKF和UKF在开始一小段时间对距离的估计存在细微的差异，致使收敛曲线不完全一致，但120 s内两曲线就趋于重合，且将测距误差收敛至200 m以下。

图2 初值有误差情况下的距离误差曲线Fig.2 The error curve of distance for biased initial value

图3 给出了在初值无误差情况下的距离误差曲线。

图3 初值无误差情况下的距离误差曲线Fig.3 The error curve of distance for precise initial value

由图3可见，在初值无误差而且测量误差很小的理想情况下，UKF和SUKF的距离误差收敛曲线比较接近，性能基本一致，而EKF收敛速度最慢，但收敛后与前两者的性能相差不大;随着测量误差的增大，UKF和SUKF的性能也基本相同，但EKF的测距精度明显差于UKF和本文算法，究其原因，测量方程(20)的非线性是较强的，EKF由于采用一阶泰勒级数展开近似，当出现大的估计误差时其线性化误差的影响也很大，因此收敛效果不佳。

总的来说，相对而言EKF对于测量误差、初始状态估计误差都很敏感;SUKF和UKF两种滤波器的性能基本一致，比EKF性能要好一些。

表1给出了不同算法完成一次时间递推平均所需的计算时间。从表1可以看出，EKF算法的运算量最小，UKF的运算量比其他两者都高，而SUKF的运算时间相比于UKF减少了约35%。

表1 不同算法的运算时间比较Table 1 Computation time cost of different algorithms

由此可见，SUKF应用到机载IRST系统被动测距问题中，具备了和UKF同样的滤波精度，但其所需要的运算时间却比UKF大大减少，非常适合于实时应用。

5 结论

本文针对机载IRST系统被动测距问题，根据系统数学模型的状态噪声和观测噪声均为加性噪声，状态方程为线性而测量方程为非线性的特点，推导了简化的UKF(SUKF)滤波算法。该算法采用较少的采样点，用UT变换解决了非线性问题，而利用卡尔曼滤波理论处理线性问题。仿真结果表明，与经典EKF相比，UKF测距精度高，并且不需要计算Jacobi矩阵，实现起来要相对容易，但以计算时间为代价。而SUKF具有与UKF几乎相同的测距精度，且SUKF能在保证滤波器性能的同时降低运算开销。因此，SUKF是一种行之有效的非线性滤波方法，更适合在机载IRST系统被动测距中应用。

［1］ 王万平，魏宏刚，廖胜，等.被动测距的可观测性分析和滤波方法［J］.红外与激光工程，2009，38(6):1083-1088.

［2］ 浦加伦，韦常柱，荣思远.修正增益卡尔曼滤波算法在被动测距问题中的应用［J］.宇航学报，2007，28(4):886-889.

［3］ LIN X，KIRUBARAJAN T，BAR-SHALOM Y，et al.Comparison of EKF，pseudomeasurement and particle filters for a bearing-only target tracking problem［C］//Proceedings of SPIE，Signal and Data Proceedings of Small Targets，2002，4728:240-247.

［4］ 程水英，邹继伟，汤鹏.免微分非线性Bayesian滤波方法评述［J］，宇航学报，2009，30(3):843-857.

［5］ JULIER S J，UHLMANN J K.Unscented filtering and nonlinear estimation［J］.Proceedings of the IEEE，2004，92(3):401-421.

［6］ 张前，王小平，林秦颖，等.扩维UKF在目标估计器中的应用［J］.电光与控制，2009，16(10):87-90.

［7］ 尹义蓉，高勇.基于UKF与融合的声探测定位与跟踪［J］.电光与控制，2010，17(12):8-12.

［8］ 邓胜利，邵雷，吴平.SINS/GPS全姿态组合导航系统的UKF 算法研究［J］.电光与控制，2010，17(12):24-28.

［9］ BOLOTIN YU V，MORCUNOVA S N.Observability with bearing-only observations and smoothness of the attainable set［J］.Journal of Mathematical Sciences，2007，147(2):6631-6637.

［10］ SHEN Mangzuo.Range information extraction from tracking data using object kinematic parameters［C］ //Proceedings of SPIE，Signal and Data Proceedings of Small Targets，1995，2561:484-488.

［11］ 陈益，赵高鹏，刘娣.简化UKF算法在摄像机标定中的应用［J］.计算机工程，2009，35(19):274-276.

［12］ 杨争斌，钟丹星，郭福成，等.一种基于高斯牛顿迭代的单站无源定位算法［J］.系统工程与电子技术，2007，29(12):2006-2009.