基于优化GM(1,1)模型的水上交通事故预测

李 杰 夏海波

（上海海事大学商船学院 中国 上海 201306）

0 引言

随着我国经济建设和社会的快速发展，贸易快速增长带来了水上运输的巨大需求，很大程度上带动了水运业的发展。水上运输也呈现出大规模、专业化的发展趋势，加之沿海水域的通航环境也更加复杂，使得在这些水域发生事故的可能性越来越高。与此同时，相关部门对水上船舶交通运输系统管理和控制的意识也逐渐加强。水上交通事故的预测的重要性愈加明显。

预测就是基于历史数据的基础上，总结出一定的规律，根据其发展趋势，从某种程度上推测事物的下一种状态。水上交通事故是小概率事件，它的发生是基于在其发展过程中变化的各种因素相互作用的结果。鉴于此，水上交通事故总体的发展水平和趋势是可以通过用适当的数学方法进行分析和预测的[1-2]。

1 预测模型的描述

1.1 灰色理论

灰色理论是1982年由邓聚龙教授提出的一种研究少数据、贫信息的不确定性问题的新方法。主要通过提取“部分”己知信息中的有价值成分，来对系统本身固有的规律进行研究[3-4]。

1.2 水上交通事故的灰色性

水上交通系统本身就非常复杂，其安全受到多方面的因素共同作用。船舶的交通事故是一种随机事件，因此具有一定的模糊性。这里，我们可以认为某一地区的船舶交通是一个灰色系统[5]。

从历年的水上交通事故统计数据不难发现，某一地区一定时期的水上交通事故数的统计数据是在一定范围内变化与时间序列有关的随机变量，因此对于一系列杂乱无章的交通事故统计数据，我们可以充分发掘其中所隐含的信息，把握其中的客观规律。利用这些规律对事故趋势的发展做出判定，而要达到这个目的，就要选择适当的预测方法，使预测的结果能够更加符合事故发展的趋势[6]。

传统预测方法有很多，诸如回归模型预测法、马尔科夫模型法以及时间序列预测方法等，一般的预测前提都是基于大量的数据，而灰色预测方法是一种新的预测方法，仅需要很少的系统信息即可实现预测。本文对传统的灰色预测方法进行进一步的组合优化，运用其对我国水上船舶交通状况进行探讨，以最近几年来船舶水上交通事故数作为模型的输入数据，来分析船舶交通事故发生的规律，由此来预测其未来可能的发展趋势。由于事故本身就是随机的概率事件，因此这里所说的预测并不是推断具体在何时何地会发生什么样的交通事故，而是从宏观上预测我国水上交通可能发展的整体状况[7]。

1.3 灰预GM(1,1)模型的一般流程[8]

（1）首先对 X（0）进行 1-AGO 累加：

对 于 时 间 序 列 X（0）有 n 个 观 察 值 ：X（0）=（x（0）（1），x（0）（2）， … ，x（0）（n）），其中，x（0）（k）≥0（k=1，2，…，n）。 对原始数据通过 1-AGO 累加生成一个新的序列 X（1）=（x（1）（1），x（1）（2），…，x（1）（n）），其中有（0）（i）（k=1，2，…，n）。

（2）检验序列 X（0）的光滑性，公式如下：

当k＞3时，若有ρ（k）＜0.5，则可以认为该序列满足准光滑性。（3）检验序列 X（1）是否具有准指数规律，公式如下：

当 k＞3 时，若有 1＜σ（1）（k）＜1.5，则可以认为该序列满足指数规律，可对 X（1）序列建立 GM（1,1）模型。

（4）对 X（1）作紧邻均值生成

Z（1）为 X（1）的紧邻均值生成序列，Z（1）=（z（1）（2），z（1）（3），…，z（1）（n）），其中有（x（1）（k）+x（1）（k-1）），k=2，3，…，n。

（6）建立一阶线性白化微分方程

和时间响应式

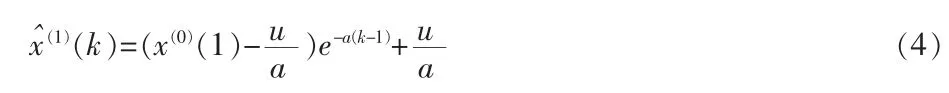
其中 k=1，2，…，n。

（7）求 X（1）的模拟值。

（8）还原后求得 X（0）的模拟值，公式如下：

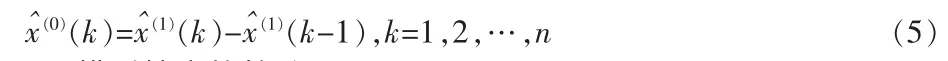
（9）模型精度的检验。

残差、相对误差的检验：

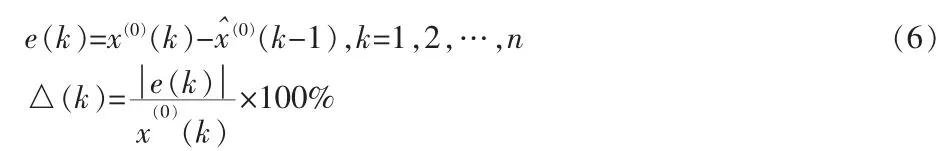
2 对GM(1,1)模型进行优化

通过对传统灰色预测流程的分析，不难发现，在通过对历史数据的累加处理后，一般都能很好的满足光滑性及准指数规律。而由步骤（5）中参数列的估计来看，其结果在一定程度上依赖于紧邻均值，因此紧邻均值的合理性直接关乎到之后的预测结果。

此处，作者从以下两方面改进传统的预测模型：1、在对原始数据进行累加之前先对其二阶弱化[9]；2、修改步骤（4）中背景值的权重[10]。

3 实例应用

由于我国海运贸易的迅速发展，加之通航条件、港口设施的不断升级，近几年来，我国的水上运输产业形势大好各大港口集装箱的吞吐量世界领先。于此同时，由于全球气候变暖，一系列极端天气诸如强台风、暴风雨等极其频繁，海啸、地震等时有发生。上述种种不利因素均对水上交通的安全构成威胁。

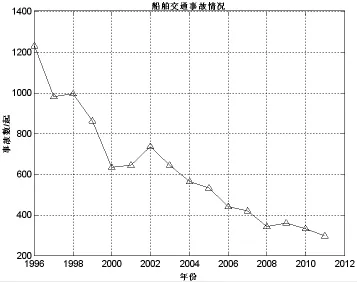
图1 近年来水上船舶交通事故情况

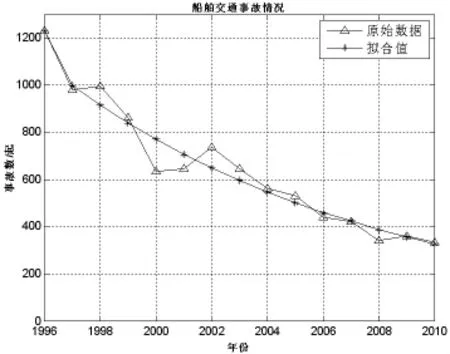
图2 优化模型与原始数据拟合情况

利用本文所优化的模型对2012年-2016年的船舶交通事故进行预测，得到表1结果。

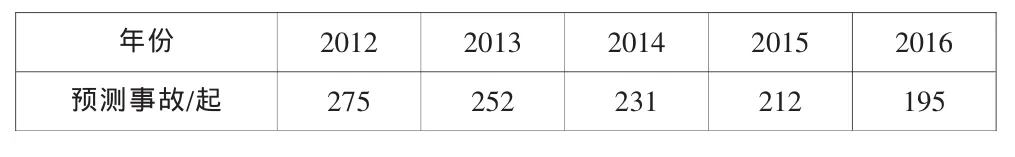
表1 2012—2016年船舶交通事故预测

上表1表明，未来5年我国水上交通发生的事故比往年有所下降，而且总统仍呈下降趋势，与历年来的实际情况相符，模型的有效性进一步得到证明。

4 结言

传统的GM(1,1)模型本身存在缺陷，对该模型的改进一直是学者们研究的热门课题[11-12]。本文在传统灰模型的基础上分别从原始数据的处理和背景值的计算两方面加以优化，在MATLAB平台上进行仿真模拟，通过近年来的水上船舶交通事故数据来验证优化模型。结果表明，优化的GM(1,1)模型在拟合情况和预测结果均达到了预期的效果，该模型可以被接受。

［1］陈崇云.我国水上交通运输安全分析及事故预测的研究[D].大连海事人学，2002.

［2］张文青，胡甚平，刘琨,等.基于熵权的海上交通风险成因物元评价模型[J].上海海事人学学报，2010，31(2)：19-22.

［3］邓聚龙.灰色理论基础[M].武汉：华中科技大学出版社，2002.

［4］刘思峰，郭天榜，党耀国.灰色系统理论及其应用[M].北京：科学出版社，1999.

［5］周丽丽，胡甚平.船舶引航风险成因灰色综合评价模型[J].上海海事人学学报，2008，29(2)：21-25.

［6］赵佳妮.用灰色马尔可夫模型预测水上交通事故量[J].交通运输工程与信息学报，2005(2)：63-67.

［7］陈咫宇，胡甚平，郝严斌.基于分形理论的水上交通事故预测[J].上海海事人学学报，2009，30(3)：18-21.

［8］吉培荣，黄巍松，胡翔勇.灰色预测模型特性的研究[J].系统工程理论与实践，2001，9：105-139.

［9］党耀国，刘思峰，刘斌，唐学文.关于弱化缓冲算子的研究[J].中国管理科学，2004，2：108-111.

［10］尚军亮，方敏.一种优化的高精度灰色GM(1,1)预测模型[J].电子与信息学报，2010，32(6)：1301-1305.

［11］张悦，李峰等.改进GM（1,1）模型在我国危险化学品事故预测中的应用[J].中国安全生产科学技术，2012，8(5)：91-95.

［12］张大海，江世芳，史开泉.灰色预测公式的理论缺陷及改进[J].系统工程理论与实践，2002，8：140-142.