TRANSPORT OF BICOMPONENT CONTAMINANT IN FREE-SURFACE WETLAND FLOW*
CHEN Bin
State Key Laboratory of Water Environment Simulation, School of Environment, Beijing Normal University, Beijing 100875, China, E-mail: chenb@bnu.edu.cn
ZENG Li, WU Yi-hong, JІ Ping, ZHAO Yi-jun
State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Іnstitute of Water Resources and Hydropower Research, Beijing 100038, China
(Received May 18, 2012, Revised October 30, 2012)
TRANSPORT OF BICOMPONENT CONTAMINANT IN FREE-SURFACE WETLAND FLOW*
CHEN Bin
State Key Laboratory of Water Environment Simulation, School of Environment, Beijing Normal University, Beijing 100875, China, E-mail: chenb@bnu.edu.cn
ZENG Li, WU Yi-hong, JІ Ping, ZHAO Yi-jun
State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Іnstitute of Water Resources and Hydropower Research, Beijing 100038, China
(Received May 18, 2012, Revised October 30, 2012)
This paper presents a theoretical analysis of a pulsed bicomponent contaminant emission into a free-surface wetland flow. The basic equations are for the bicomponent contaminant transport in the wetland flow under the combined action of advection, mass dispersion, and ecological reaction at the phase averaged scale. The effect of the ecological reaction is separated from the hydrodynamic effect via a set of widely used transforms. The analytical solution for the evolution of the depth-averaged concentration is rigorously derived, with a limiting case covering the known solution for the single component contaminant transport. Іt is found that the depth-averaged species concentration of the bicomponent contaminant can approach an equilibrium state determined by the distribution coefficient.
contaminant dispersion, bicomponent contaminant, wetland hydrodynamics, environmental risk assessment
Introduction
The wetlands play a variety of roles in terms of water purification, flood control, drought resistance, and biodiversity conservation[1-9]. For an environmental risk assessment and a restoration program related to the wetlands, the essential issue is to predict the contaminant transport under the combined action of advection, mass dispersion and ecological reaction at the phase average scale[10,11].
With respect to the contaminant transport in a wetland flow, some theoretical studies were carried out based on the Taylor’s classic analysis on the dispersion, the method of concentration moments, and the multi-scale analysis. Lightbody and Nepf proposed a formula for predicting the longitudinal dispersion coefficient for a wetland flow dominated by the emergent vegetation[12,13]. Based on the Taylor’s analysison the dispersion and the method of concentration moments, Chen et al.[10], Zeng et al.[11,14-17]and Wu et al.[18,19]obtained some analytical solutions of the environmental dispersivities for a single zone wetland flow under various conditions. Murphy et al.[20]and Nepf et al.[21]investigated the behavior of the longitudinal dispersion due to the turbulence at different scales. Analytical solutions of the environmental dispersivities were also obtained for a two-layer wetland flow and a two-zone wetland flow[22,23]. However, these analytical solutions concern only the evolution of a single component contaminant, not so much the behavior of the bicomponent contaminant, due to the complexity of the hydraulic dispersion and the ecological reaction[24-28].
For the typical case of a pulsed bicomponent contaminant discharge into a free surface wetland flow, this paper comes up with an analytical solution of the depth-averaged concentration under the conditions of the hydraulic dispersion and the ecological reaction. The specific goals are: (1) to introduce the general equations for the bicomponent contaminant transport in the wetland flow, and (2) to present ananalytical solution for the long time evolution of the depth-averaged concentration of the bicomponent contaminant.
1. Formulation
For a typical wetland flow, the governing equations for mass transport of the bicomponent contaminant can be written as[10,11,29]

where φ is the porosity, t the time,AC the concentration of contaminant A, u the velocity, κ the tortuosity, λ the mass diffusivity, K the mass dispersivity tensor,Ar the ecological reaction rate of contaminant A,dk the distribution coefficient,BC the concentration of contaminant B, andBr the ecological reaction rate of contaminant B. The last term on the right hand side of Eqs.(1) and (2) represents the interaction between pollutants A and B.

Fig.1 Schematic diagram of a free water surface wetland flo w
Consider the bicomponent contaminant transport in a unidirectional free-surface wetland flow in a Cartesian coordinate system with coordinate axes coinciding with the principle axes of the tensor K, the longitudinal x-axis along the flow direction, the vertical z-axis upward, and the origin at the bottom, as shown in Fig.1. The corresponding velocity profile can be expressed as[11]

where U is the depth-averaged velocity, α is a dimensionless parameter representing the combined action of the depth, the vertical momentum dispersion, the microscopic curvature of the flow passage, and the viscous friction of vegetation[11], and H is the depth of the wetland.
Consider a uniform instantaneous emission of the bicomponent contaminant at the cross-section of =x 0 at time =0t, with the initial condition as

where Q is the mass per unit width, and ()xδ is the Dirac delta function.
For the two-dimensional process, Eqs.(1) and (2) reduce to
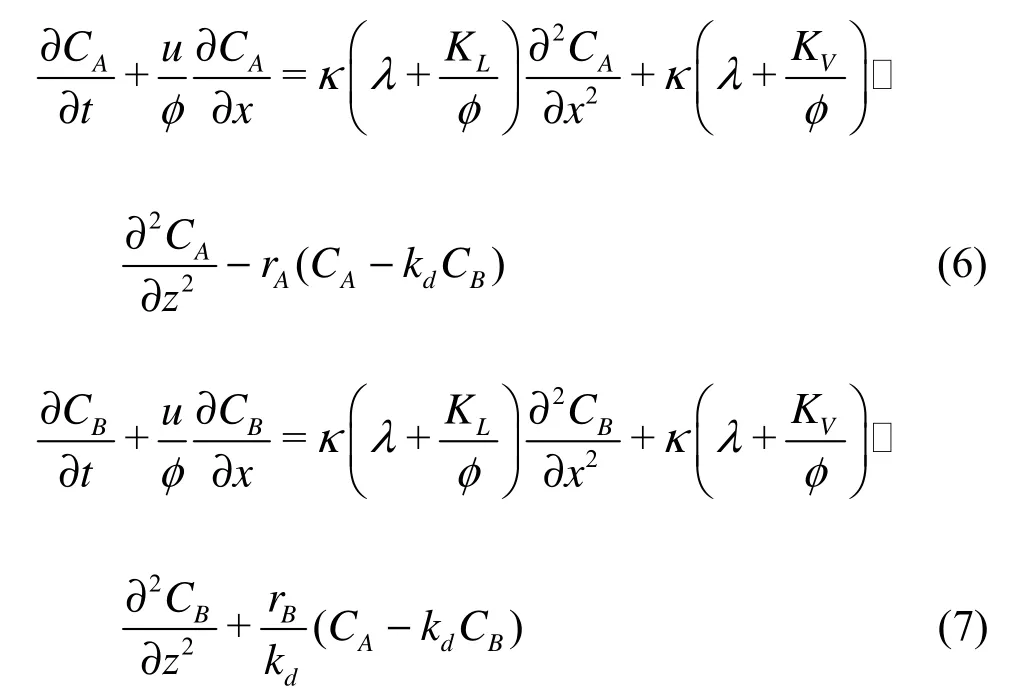
respectively, whereLK andVK are the longitudinal and the vertical mass dispersivities, respectively. For a finite contaminant discharge, the concentration boundary conditions at =x±∞ are

For the bottom bed at z=0 and the free surface at z=H, the concentration boundary conditions are
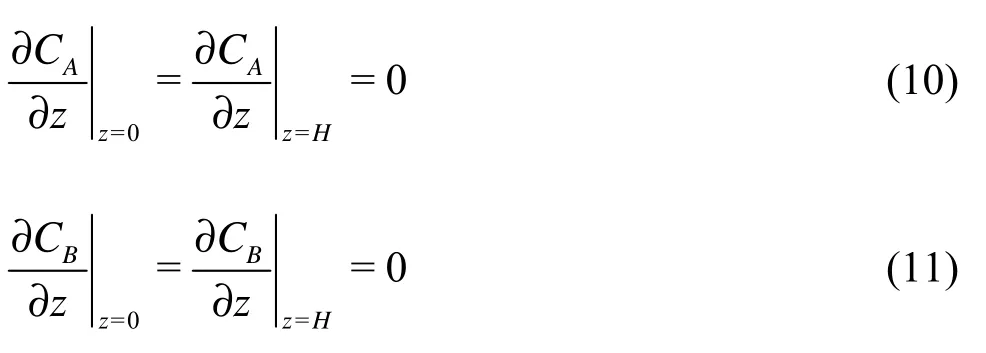
With the dimensionless parameters defined as

the governing equations, as well as the boundary and the initial conditions can be rewritten as

where

2. Separation of ecological reaction effect from hydrodynamic effect
The method for solving the second-order constant-coefficient linear parabolic system in Ref.[30] is adopted, with the effect of the ecological reaction being separated from the hydrodynamic effect. With the transform introduced in Ref.[30]

where ε=NB/NA, Eqs.(13) and (14) of an advection-diffusion-reaction type for the concentration become

respectively. Eqs.(17) and (18) represent a physical process of the advection-diffusion with various initial conditions.
The solution of Eqs.(17) and (18) can be rewritten as


Since ψ varies with ζ, it is difficult to obtain the exact analytical solution of Θ. For the environmental risk assessment associated with the wetland flow, the main concern is the long time evolution of the contaminant. According to Zeng and Chen’s results, the depth-averaged concentration satisfies[11]
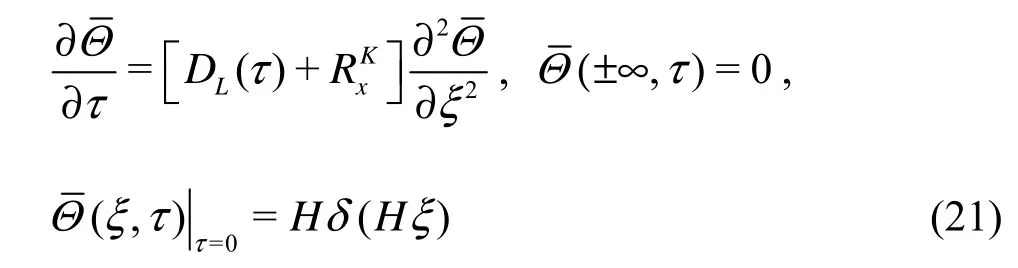
whereLD is the environmental dispersivity expressed as

The solution of Eq.(21) is[11]

where

3. Results and discussions
The solution for the long time evolution of the depth-averaged concentration of the bicomponent contaminant can be expressed as




Fig.2 Variations of ΨAEand ΨBEwith ξ for τ=15.0, α=1.0, Pex=1.0, φ=0.9, RxK=0.1, NA=1.0, kd=2.0 and ε=0.1, 0.5, 1.0, 2.0, 4.0 and 8.0
This result shows that the species concentration of the bicomponent contaminant will reach an equilibrium state, and the ratio of the depth-averaged concentration of pollutant A to that of pollutant B is determined bydk. Figure 2 shows the variations ofΨAEand ΨBEwith ξ for τ=15.0, α=1.0, Pex= 1.0, φ=0.9,=0.1, NA=1.0, kd=2.0and ε= 0.1, 0.5, 1.0, 2.0, 4.0, and 8.0. Іt is shown that the concentration of pollutant A is just twice that of pollutant B for kd=2.0.
Acknowledgement
This work was supported by the Special Foundation of China Іnstitute of Water Resources and Hydropower Research (Contract No. SJ1239).
[1] CHEN Z. M., CHEN B. and CHEN G. Q. Cosmic exergy based ecological assessment for a wetland in Beiing[J]. Ecological Modelling, 2011, 222(2): 322-329.
[2] WU Z., ZENG L. and CHEN G. et al. Environmental dispersion in a tidal flow through a depth-dominated wetland[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(12): 5007-5025.
[3] CHEN G., WU Z. Taylor dispersion in a two-zone packed tube[J]. International Journal of Heat and Mass Transfer, 2012, 55(1-3): 43-52.
[4] WU Z., CHEN G. Dispersion in a two-zone packed tube: An extended Taylor’s analysis[J]. International Journal of Engineering Science, 2012, 50(1): 113-123.
[5] CHEN G., SHAO L. and CHEN Z. et al. Low-carbon assessment for ecological wastewater treatment by a constructed wetland in Beijing[J]. Ecological Engineering, 2011, 37(4): 622-628.
[6] CHEN Z., CHEN G. and CHEN B. et al. Net ecosystem services value of wetland: Environmental economic account[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(6): 2837-2843.
[7] CHEN B., CHEN G. Emergy-based energy and material metabolism of the Yellow River basin[J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(3): 923-934.
[8] CHEN G., JІ X. Chemical exergy based evaluation of water quality[J]. Ecological Modelling, 2007, 200(1-2): 259-268.
[9] HUANG L., CHEN G. and ZHANG Y. et al. Exergy as a unified measure of water quality[J]. Communications in Nonlinear Science and Numerical Simulation, 2007, 12(5): 663-672.
[10] CHEN G., ZENG L. and WU Z. An ecological risk assessment model for a pulsed contaminant emission into a wetland channel flow[J]. Ecological Modelling, 2010, 221(24): 2927-2937.
[11] ZENG L., CHEN G. Ecological degradation and hydraulic dispersion of contaminant in wetland[J]. Ecological Modelling, 2011, 222(2): 293-300.
[12] LІGHTBODY A. F., NEPF H. M. Prediction of velocity profiles and longitudinal dispersion in emergent salt marsh vegetation[J]. Limnology and Oceanography, 2006, 51(1): 218-228.
[13] LІGHTBODY A. F., NEPF H. M. Prediction of nearfield shear dispersion in an emergent canopy wiht heterogeneous morphology[J]. Environmental Fluid Mechanics, 2006, 6(5): 477-488.
[14] ZENG Li. Analytical study on environmental dispersion in wetland flow[D]. Doctoral Thesis, Beijing: Peking University, 2010(in Chinese).
[15] ZENG L., CHEN G. and TANG H. et al. Environmental dispersion in wetland flow[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(1): 206-215.
[16] ZENG L., CHEN G. and WU Z. et al. Flow distribution and environmental dispersivity in a tidal wetland channel of rectangular cross-section[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(11): 4192-4209.
[17] ZENG L., WU Y. and JІ P. et al. Effect of wind on contaminant dispersion in a wetland flow dominated by free-surface effect[J]. Ecological Modelling, 2012, 237-238: 101-108.
[18] WU Z., LІ Z. and CHEN G. Multi-scale analysis for environmental dispersion in wetland flow[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(8): 3168-3178.
[19] WU Zi, LІ Zhi and ZENG Li et al. Environmental dispersivity in free-water-surface-effect dominated wetland: Multi-scale analysis[J]. Frontiers of Environmental Science and Engineering in China, 2011, 5(4): 597-603.
[20] MURPHY E., GHІSALBERTІ M. and NEPF H. Model and laboratory study of dispersion in flows with submerged vegetation[J]. Water Resources Research, 2007, 43(5): W05438.
[21] NEPF H., GHІSALBERTІ M. and WHІTE B. et al. Retention time and dispersion associated with submerged aquatic canopies[J]. Water Resources Research, 2007, 43(4): W04422.
[22] CHEN G., WU Z. and ZENG L. Environmental dispersion in a two-layer wetland: Analytical solution by method of concentration moments[J]. International Journal of Engineering Science, 2011, 51: 272-291.
[23] WU Z., CHEN G. and ZENG L. Environmental dispersion in a two-zone wetland[J]. Ecological Modelling, 2011, 222(3): 456-474.
[24] CHІBAN M., SOUDANІ A. and SІNAN F. et al. Single, binary and multi-component adsorption of some anions and heavy metals on environmentally friendly Carpobrotus edulis plant[J]. Colloids and Surfaces BBiointerfaces, 2011, 82(2): 267-276.
[25] FEREІDOUNІ M., DANESHІ A. and YOUNESІ H. Biosorption equilibria of binary Cd(ІІ) and Ni(ІІ) systems onto Saccharomyces cerevisiae and Ralstonia eutropha cells: Application of response surface methodology[J]. Journal of Hazardous Materials, 2009, 168(2-3) :1437-1448.
[26] ZІAGOVA M., DІMІTRІADІS G. and ASLANІDOU D. et al. Comparative study of Cd(ІІ) and Cr(VІ) biosorption on Staphylococcus xylosus and Pseudomonas sp. in single and binary mixtures[J]. Bioresource Technology, 2007, 98(15): 2859-2865.
[27] SAĞ Y., YALCUK A. and KUTSAL T. Mono and multi-component biosorption of heavy metal ions on Rhizopus arrhizus in a CFST[J]. Process Biochemistry, 2000, 35(8): 787-799
[28] GONNELLA G., LAMURA A. Long-time behavior and different shear regimes in quenched binary mixtures[J]. Physical Review E, 2007, 75(1): 011501.
[29] VAFAІ K. Handbook of porous media[M]. Boca Ratton, USA: CRC Press, 2005, 81-140.
[30] POLYANІN A. D., MANZHІROV A. V. Handbook of mathematics for engineers and scientists[M]. Boca Raton, USA: CRC Press, 2007.
* Project supported by the National Natural Science Foundation of China (Grant Nos. 10972009, 50939001 and 41271543).
Biography: CHEN Bin (1972-), Male, Ph. D., Professor
- 水动力学研究与进展 B辑的其它文章
- REVIEW OF SOME RESEARCHES ON NANO- AND SUBMICRON BROWNIAN PARTICLE-LADEN TURBULENT FLOW*
- EFFECT OF A PROPELLER AND GAS DIFFUSION ON BUBBLE NUCLEI DISTRIBUTION IN A LIQUID*
- APPLICATION OF QUADRATIC AND CUBIC TURBULENCE MODELS ON CAVITATING FLOWS AROUND SUBMERGED OBJECTS*
- THE HYDRODYNAMIC CHARACTERISTICS OF FREE VARIABLEPITCH VERTICAL AXIS TIDAL TURBINE*
- NUMERICAL PREDICTION OF SUBMARINE HYDRODYNAMIC COEFFICIENTS USING CFD SIMULATION*
- SIMULATION OF OIL-WATER TWO PHASE FLOW AND SEPARATION BEHAVIORS IN COMBINED T JUNCTIONS*

