NUMERICAL INVESTIGATION OF FLOW PATTERNS IN DIFFERENT PUMP INTAKE SYSTEMS*
ZHAN Jie-min, WANG Ben-cheng, YU Ling-hui
Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275, China,
E-mail: cejmzhan@gmail.com
LI Yok-sheung
Department of Civil and Structural Engineering, The Hong Kong Polytechnic University, Hong Kong, China TANG Ling
Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275, China
(Received April 23, 2012, Revised October 11, 2012)
NUMERICAL INVESTIGATION OF FLOW PATTERNS IN DIFFERENT PUMP INTAKE SYSTEMS*
ZHAN Jie-min, WANG Ben-cheng, YU Ling-hui
Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275, China,
E-mail: cejmzhan@gmail.com
LI Yok-sheung
Department of Civil and Structural Engineering, The Hong Kong Polytechnic University, Hong Kong, China TANG Ling
Department of Applied Mechanics and Engineering, Sun Yat-sen University, Guangzhou 510275, China
(Received April 23, 2012, Revised October 11, 2012)
A 3-D numerical model for pump intake is established based on the Navier-Stokes equations with the RNG kεturbulence model and the VOF method to simulate the free surface. The applicability of the proposed model is validated by a test case of non-symmetric pump-intake bay. The predicted locations, structures and shapes of all vortices are in good agreement with those observed in experiments, though with some differences in vorticity strengths. The flow pattern and the efficiency of five types of pump intake systems are studied. The discharge and the velocity uniformity of the intake system are used as indices to evaluate its performance.
pump intake, Navier-Stokes equations, VOF method
Introduction
The riverside intakes for power plant cooling water, agricultural, municipal and industrial water supply systems, and other similar occasions, are often plagued by sediment deposition. They are also often beset by low efficiency due to vortices, spiral flows and large-scale reverse flows, which occur on the inlet side of a pump intake system. The flow patterns near pump intakes and their effects on the pump operation have attracted much research attention.
Rajendran et al.[1]carried out experiments to validate a numerical model designed to simulate the 3-D turbulent flow in a pump-intake bay. The experiments involve the flow visualizations and the measurements with the Particle Image Velocimetry (PIV). The numerical model consists of solving the Reynolds Averaged Navier-Stokes (RANS) equations with a near-wall turbulence model. The predicted number,locations, and general structures of vortices were found in good agreement with those observed in the experiments. However, the vortices were generally larger and weaker than the measured ones. These differences were attributed to the unsteadiness of the flow and the inadequacy of the turbulence model. The technical note of Constantinescu and Patel[2]concerns with the role of the turbulence model and the influence of the wall roughness in the prediction of locations, sizes and strengths of different types of vortices, and the level of swirl in the intake pipe. Rajendran and Patel[3]continued their experiments described in Rajendran et al.[1]aiming at improving the understanding of vortices formed in pump intake bays. Depending on the submergence of the intake pipe and its position relative to the channel walls, some vortices were found in well-defined mean positions, while others were intermittent or in bimodal behavior. The experiments clearly demonstrated the usefulness of the PIV in obtaining quantitative information about the number, locations, sizes, and strengths of vortices formed and in validating numerical models of pump intake flows.
Chen and Pater[4]carried out a computational experiment to study the performance of different nearwall treatments in a turbulence model. These tests enabled the evaluation of the performance of different approaches in simulating flows involving longitudinal and transverse surface curvatures, streamwise and normal pressure gradients, viscous-inviscid interaction, and separation. Constantinescu and Patel[5]presented a computational fluid dynamics model to simulate the three-dimensional flow field in a pump intake and to study the formation of free-surface and wall-attached vortices. A two-layer kε- turbulence model was employed to resolve the near-wall flow that was critical to the description of wall-attached vortices. Montazerin et al.[6]presented a numerical study of the flow field in a horizontal intake without rotational effects. The critical condition was predicted from a continuous zero pressure line from the free surface to the intake. Marghzar et al.[7]presented the results of a numerical simulation of a vertically downward intake. The RANS equations and the turbulence closure equations were used. Both the free surface and the subsurface vortices were identified and their strengths and locations estimated. The acceleration length for the vertical velocity component close to the pipe was found to be about twice the pipe size, as in close agreement with the predicted results for the axial component in horizontal intakes. Ma et al.[8]applied a commercially available, 3-D computational fluid dynamics model to simulate the flow structure in an upland river that was prone to flooding. The simulations used a rectangular channel geometry, smooth sidewalls and a bed topography obtained from the field site that containing a subdued pool-riffle sequence. Tang et al.[9]presented a Lattice Boltzmann Method (LBM) coupled with a Sub-Grid Stress (SGS) model for simulating flows in a pumping station forebay. The model successfully predicted the flow characteristics in a pumping station forebay, such as the secondary flow, the vortex and the water level.
Marghzar et al.[10]presented a study of the flow structure and the turbulence characteristics of a horizontal water intake. Along with experimental investigations with a laser Doppler anemometer, a 3-D numerical code for the prediction of any gravitational turbulent flow was also developed, making the measurements and the predictions of the critical condition and its corresponding water level possible. The notable observation was that the critical condition in this symmetrical intake occurred with no swirl on the free surface. Ansar and Nakato[11]made detailed measurements of 3-D turbulent flows within a rectangular single-pump bay area of a right-angle water intake model with and without cross flow using an Acoustic Doppler velocimeter (ADV) in order to elucidate the swirling flow characteristics within the pump sump. The pump-approach flow distributions were characterized by different velocities. The uncertainty analysis of the ADV velocity measurements showed good quality data. These experimental data were utilized in validating the inviscid numerical solutions. Li et al.[12]developed and validated a non-hydrostatic 3-D numerical model consisting of solving the RANS equations with two-equation turbulence models and using the unstructured grid with flexible mesh cell shapes. The flow in a relatively simple laboratory intake model, with a straight vertical pump column, was simulated and the results were compared with experimental data to validate the numerical model. Tokyay and Constantinescu[13]developed a reliable numerical model to predict the pump intake flow and the associated vortices. The Large-Eddy Simulation (LES) in conjunction with an accurate non-dissipative non-hydrostatic Navier-Stokes massively parallel solver was used to predict the flow and vortical structures in a pressurized pump intake of complex geometry. The LES model was validated using the PIV data collected on a laboratory model of the pump intake with a realistic geometry. Nakayama and Hisasue[14]simulated the 3-D unsteady flow in an intake channel of a small-scale hydroelectric power facility using the LES method. The free-surface depression associated with the formation of a free-surface vortex and its time development were particularly well captured. Skerlavaj et al.[15]made twelve steady-state and transient simulations on a fine computational mesh, using different turbulence models, namely the Shear Stress Transport (SST), the Scale-Adaptive Simulation (SAS), the Reynolds stress model, the explicit algebraic Reynolds-stress model, the detached eddy simulation and the LES. The Curvature-Correction (CC) option was assessed with the SST and SAS turbulence models. Good agreement with experimental results was shown for a longer simulation with the SAS-CC turbulence model.
1 . Mathematical formulations
1.1 Governing equations
The hydrodynamics problem studied in this paper is the inlet flow pattern and the efficiency of a pump intake. The RANS equations and the RNG k-ε turbulence model are used to simulate the flowof an incompressible, viscous fluid. The VOF method is adopted to capture the fluctuating water surface.
1.1.1 RANS equations
For a turbulent flow, the instantaneous velocity andthe pressure can be decomposed into two parts: the mean velocity and pressure,and, and the corresponding fluctuating components, ui' and p'.in which the subscript i=1, 2 and 3 for a 3-D flow.


F ig.1 Configuration of water-pump intake model
The mean flow field is governed by the RANS equations as follows:

where ρis the density of fluid,giis theith component of the gravitation acceleration andμ is the coefficient of viscosity,is the Reynolds stress, which represents the effects of the turbulent flow on the mean flow field.
1.1.2 Turbulence model
To appropriately model the Reynolds stress, the RNGk-ε model based on the renormalizationgroup methods is employed. The turbulence kinetic energy k and its rate of dissipationε are obtained from the following transport equations:


where Gkrepresents the generation of the turbulent kinetic energy due to the mean velocity gradients, Gbis thegeneration of the turbulent kinetic energy due to the buoyancy,YMis the contribution of the fluctuating dilatation in the compressible turbulence to the overall dissipation rate, αkandαεare the inverse effective Prandtl numbers, C1ε=1.42 and C2ε= 1.68 are the empirical constants and μeffis the effective viscosity.
Comparing with the stan dard k -ε model, the RNG model has made the following refinements: (1) it has an additional term in itsε equation which improves the accuracy for rapidly strained flows, (2) the effect of the swirl on the turbulence is included in the model, thus the accuracy for swirling flows is enhanced, and (3) an analytical formula for the turbulent Prandtl number is provided, while the standard model uses user-specified constant values. These improvements render the RNG k-ε model more accurate and reliable fora wider class of flows than the standard k-ε model[16].
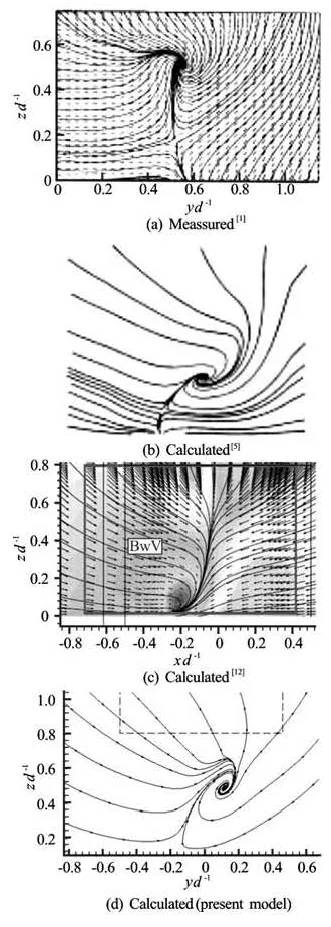
Fig.2 Attached vortex at a distance 0.23d from back wall
1.1.3 Volume Of Fluid (VOF) method
The free surface is captured by the VOF method. The volume fraction functionFqis defined as the ratio of the volume occupied by the qthphase in a cell to the total volume of the cell. For two-phase problems, q=1 or 2 since there are only two phases, namely, the air and the water. Fqis determined by the following equations:

The density andthe viscosity in the transport equations are determined by the component phases in each control volume as follows:

1.2 Boundary and initial conditions
In the present model, the intake pump is simplified as an infinitely thin interior face, called the fan boundary, in the suction pipe. A discontinuous pressure jump across the fan, which drives the water through the intake pipe, is specified as a constant in the present study. The pressure jump is related to the power of the intake pump.

Fig.3 Attached vortex in plane 0.25d from sidewall 2

Fig.4 Attached vortex in plane 0.15dfrom sidewall 1
The inlet is set at the upstream of the pool. It is assumed that the discharge is determined by the power of the pump. The inlet velocity boundary condition is to let the velocity gradient equal to zero

1.3 Evaluation of pump efficiency
1.3.1 Pu mp discharge
Apump provides energy to the water. Most of the energy will be transformed to the kinetic energy and the potential energy of thewater and a small amount will be dissipated due tothe friction and the turbulence, which iscalled the hydraulic loss. The power of the pump is ΔpQ, the sum of the kinetic energy and the potential energy of the water at the outlet of the intake pipe is, and the hydraulic loss can be equivalently written as Δp'Q , where Q is the discharge of the intake pipe, v is the average velocity at the intake pipe,v=Q/A.

Fig.5 Free-surface vortex
Due to the conservation of energy,

Wer ewrite this formula as

For a constant pressure jump, Δp, the larger the flow isin the intake pipe, the smaller the hydraulic loss in the intake system will be.
1.3.2 Velocity uniformity
The uniformity of velocityin the suction pipe has a direct influence on the efficiency of a pump. In the present study, the velocity uniformity is used to evaluate the efficiency of the pump. The more uniform the velocity is, the moreefficient the pump will be. The velocity uniformity, η, based on the mass-weighted average axial velocity, is defined as
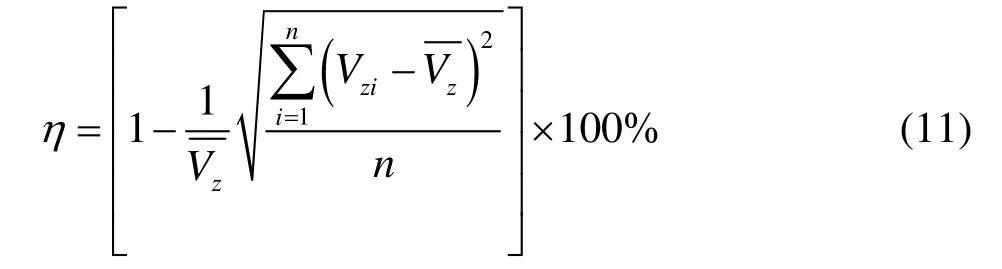

whereVziand dAiare the axial velocity and the corresponding areaof the mesh element in the crosssection andnis thenumber of mesh elements in the cross-section.
1.4 Numerical proce dure
The Pressure Staggering Option (PRESTO) discretization scheme is used for the pressure. The Quadratic Upwind Interpolation of Convective Kinematics (QUICK) algor ithm is used for the momentum and turbulence equations. TheSemi-Implicit Method for Pressure Linked Equations (SIMPLE) algorithm is used for the pressure-velocity coupling. A geometric reconstruction scheme for the VOF model is employed.
2. Model validation
The pump intake model used in experiments and numerical simulations by Rajendran et al.[1]is employed inthis section to validate the numerical model. Figure 1 shows the schematic diagram of the pump intake system. The dimensions of the intake are: the intake pipe diameter d =0.088m, L=12.8d, L1= 2.15d, L2=1.35d, X=0.9d, S=1.6d and C= 0.8d. The discharge Q is 0.003 m3/s. The numerical model has 760 000 computational cells.

Fig.6 Vortex in plane 0.25d from the floor

Fig.7 Different types of pump intake systems
Figure 2 shows the streamlines in a plane at a distance of 0.23d from the back wall. The numerical solutions predict the general structure and thelocation ofthevortex well. This result is better thanthat obtained by Constantinescu and Patel[5], but thepredictedstrength of the maximum vorticity at the vortex center is 3.0,which is larger than the measured value of 2.3. Figure 3 shows the results for the attached vortex in the plane 0.25d from the sidewall 2. A good agre ement is se en b etween the experim ental and numericalresultsintheshape,thelocationandthe s ize ofthe vortex, but the maximum strength of vorticity at the vortex center is also over-predicated, which is1.7 in contrast to the experimental value of 1.3. Figure 4 shows the results for the attached vortex in the plane 0.15d from the sidewall 1. The experimental and numerical results are in good agreement with respect to the general flow structure, but the vortex shape calculated is flatter than that measured. The strength of the maximum vorticity at the vortex center is under-predicated, which is 0.42 in contrast to the experimental value of 0.8. The free-surface vortex in the plane 0.16d below the free surface is shown in Fig.5. The present solution results show a clear improvement over those obtained by Constantinescu and Patel[5]. Figure 6shows the vortex in the plane 0.25d from the floor. The experimental and numerical results are in good agreement in the structure and the size of the vortex. The measured value of the maximum vorticity is -4.9, while the predicted value in the present model is -3.3 and that predicted by Ref.[5] is -2.0.
3. Different types of pump intakes
In this work, five different pump intake systems, namely, three lateral intake systems (LI1, LI2 and LI3) and two front intake systems (FI1 and FI2), are considered to study the flow patterns near the pump intakes and their effects on the pump operation. The configurations of the five different intake systems are shown in Fig.7.
There are three pumps in each configuration. The pressure jump for all pumps is specified as 2 400 Pa and the water depth h=0.84m. The distance between the pipe-inlet and the floor is 0.12 m. The discharges of LI1, LI2, FI1 and FI2 are determined by the pressure jump of the pump in the computation.

Fig.8 Streamlines of different pump intake systems at Z =0.08m
In system LI3, the flow from the inlet will split into two parts at the channel junction. One part will flow to the pump-intake bay and the discharge is determined by the power of the pump as in other intake systems. The other part will flow to the branch channel downstre am . So in FI3 , four diffe rent dischar3ges arespecifiedattheinletboundary,Q=50 m/h, 100 m3/h, 150 m3/h and 200 m3/h. The static pressure and the constant water depth h=0.84m aregiven at theoutletofthebranchchannel.Theflowpatternand the efficiency of the pump will be compared in these cases. From Figs.8 and 9, and Tables 1 and 2, it can be seen that there are no large differences in the pump discharge and the velocity uniformity between FI1 and FI2. However, there are large differences in the flow patterns near the pump intakes between the lateral and the front intake systems. There are some vortices near the corners of the two lateral intakes, LI1 and LI2. The vortex near pump 1 is bigger than that near pump 2. No vortex is generated by pump 3. From Tables 1 and 2, pump 3 has a slightly larger pump discharge and a better uniformity. For the front intake systems, FI1 and FI2, no vortex is generated by the pumps. There is no large difference in the velocity uniformity between lateral and front intake systems. However, the characteristics of LI3 are more complicated. For the case of LI3-50, about one half of the total pump discharge is from the upstream channel and the other half is from the branch channel. There are only small vortices in the forebay generated by pump 1 and pump 3. A slightly larger total pump discharge and a better uniformity are achieved than those of LI1 and LI2. For the case of LI3-100, the total pump discharge is roughly the same as that of LI3-50. The flow pattern is similar to those of LI1 and LI2. Only a small quantity of water is drawn from the branch channel, in contrast to LI3-50. The water flow rates in the upstream channel in cases of LI3-150 and LI3-200 are much higher than the total pump discharge. The vortices in the forebay are generated by all three pumps and their sizes are larger than corresponding ones in other lateral intake systems. The total pump discharge is smaller and the velocity uniformity deteriorates in these two cases. The computed results of the four cases of LI3 show that when the flux in the upstream channel is smaller than the target of the total pump discharge, the branch channel can play the role of a secondary source of water.
4. Conclusions
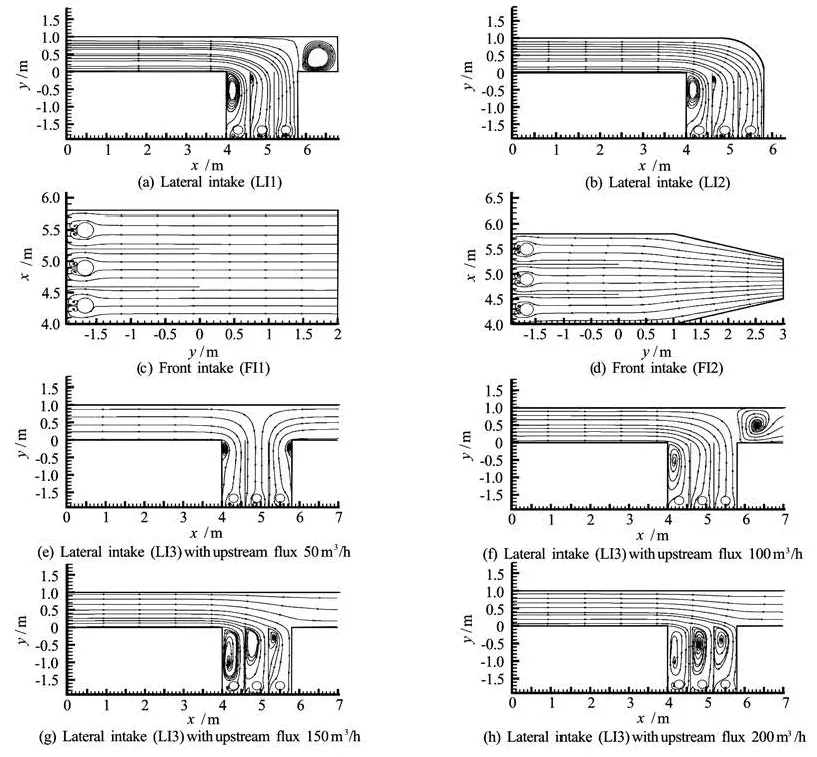
Fig.9 Stream lines of different pump intake systems at Z =0.78m

Table 1 Pump discharge in different intake systems
In this paper, a numerical model based on the RANS equations with the RNG kε- turbulence closure model and the VOF method is proposed. The model is first validated by using a non-symmetric pump-intake bay where experimental results wereprovided by Rajendran et al.[1]. The numerical results are in good agreement with the experimental data on locations, structures, shapes and sizes of all the vortices. The agreement is better than the calculation results of Constantinescu and Patel[5]. The improvement can be attributed mainly to the better performance of the RNG kε- turbulence model.
Free-surface vortices often occur in an intake pump system (Fig.5). Those free-surface vortices will induce the air-entraining phenomenon if the intake submergence is lower than the critical submergence. However, in the present study, only high submergence is considered, S/d=1.6 in Section 2 and S/d= 3.0 in Sectio n 3, both higher thanthe critical submergence. So, the air-entraining is not considered in this work.
The numerical model is then applied to study five different pump intake systems, each with three pumps. For l ateral i ntake sy stems, the perform an ce o f the threepumpscanbedifferentbecauseoftheflowpatterns, especially due to the vortices near the corners of the inlet channel and theintake bay. The efficiencies of the three pumps in the two front intake systems are the same. The characteristics of the lateral intake system LI3 is more complicated than other systems because of the addition of a branch channel. It is shown that when the upstream flux is smaller than the target of the total pump discharge, the branch channel can play the role of a secondary source of water. It is generally known that asymmetries will enhance the possibility of forming vortices, resulting in undesirable flow patterns, which will reduce the efficiency of a pump intake system. Asymmetries include the asymmetry of the intake pump structure, such as the validation case described in Section 2, and the asymmetry of the upstream flow, such as the lateral intake case considered in Section 3. In order to reduce the strength of the vortex, the intake pump structure and the upstream flow should be made as symmetrical and uniform as possible. In lateral cases LI3-50 and LI3-100, the upstream flow is made more symmetrical and uniform by addition of a branch channel, resulting in higher efficiency of the pump intake system. However, in cases LI3-150 and LI3-200, the symmetry and uniformity of the flow are not improved, and hence the performances of the pump intake system are undesirable.

Table 2 Velocity uniformity of different intake systems
Acknowledgement
This worked was supported by the Hong Kong Polytechnic University (Grant No. H-ZG68).
[1] RAJENDRAN V. P., CONSTANTINESCU S. G. and PATEL V. C. Experimental validation of numerical model offlow in pump-intake bays[J]. Journal of Hydraulic Engineering, ASCE, 1999, 125(11): 1119- 1125.
[2] CONSTANTINESCU G. S., PATEL V. C. Role of turbulence model in prediction of pump-bay vortices[J]. Journal of Hydraulic Engineering, ASCE, 2000, 126(5): 387-391.
[3] RAJENDRAN V. P., PATEL V. C. Measurement of vortices in model pump-intake bay by PIV[J]. Journal of Hydraulic Engineering, ASCE, 2000, 126(5): 322-334.
[4] CHEN H. C., P ATER V. C. Near-wall turbulence models for complex flows includingseparation[J]. AIAAJournal, 1988, 26(6): 641-648.
[5]CONSTANTINESCU G. S.,PATEL V. C. Numerical modelfor simulation of pump-intake flow and vortices[J]. Journal of Hydraulic Engineering, ASCE, 1998, 124(2): 123-134.
[6]MONTAZERIN N., RAHIMZADEH H. and MARGHZAR S. H. Prediction of critical condition at a horizontal intake through pressure contours[C]. Proceeding of the XIV IAHR Congress in Hydraulics. Beijing, China, 2001, 434-441.
[7] MARGHZAR S. H., MONTAZERINN. and RAHIMZADEH H. Numerical simulation of asymmetric flow in a vertically downward intake[C]. Advances in fluid mechanics IV, 4th International on Advances in Fluid Mechanics. Southampton, UK, 2002, 537-546.
[8] MA L., ASHWORTH P. J. and BEST J. L. et al. Computational fluid dynamics and the physical modelling of an upland urban river[J]. Geomorphology, 2002, 44(3- 4): 375-391.
[9] TANG Xue-lin, WANG Wu-chang and WANG Fu-jun. Application of LBM-SGS model to flows in a pumping station forebay[J]. Journal of Hydrodynamics, 2010, 22(2): 196-206.
[10]MARGHZAR S. H., MONTAZERIN N. and RAHIMZADEH H. Flow field, turbulence and critical condition at a horizontal water intake[J]. Proceedings of the Institution of Mechanical Engineers Part A-Journal of Power and Energy, 2003, 217(1): 53-62.
[11] ANSAR M.,NAKATO T. Experimental study of 3D pump-intake flows with and without cross flow[J]. Journal of Hydraulic Engineering, ASCE, 2001, 127(10): 825-834.
[12] LI S. H., LAI Y. and WEBER L. et al. Validation of a three-dimensional numerical model for water-pump intakes[J]. Journal of Hydraulic Research, 2004, 42(3): 282-292.
[13]TOKYAY T. E., CONSTANTINESCU S. G. Validation of a large-eddy simulation model to simulate flow in pump intakes of realistic geometry[J]. Journal of Hydraulic Engineering, ASCE, 2006, 132(12): 1303- 1315.
[14] NAKAYAMA A., HISASUE N. Large eddy simulation of vortex flow in intake channel of hydropower facility[J]. Journal of Hydraulic Research, 2010, 48(4): 415-427.
[15] ŠKERLAVAJ A., ŠKERGET L. and RAVNIK J. et al. Choice of a turbulence model for pump intakes[J]. Proceedings of the Institution of Mechanical Engineers Part A-Journal of Power and Energy, 2011, 225(6): 764-778
[16] ZHAN J. M., DONG Z. and JIANG W. et al. Numerical simulation of wave transformation and runup incorporating porous media wave absorber and turbulence models[J]. Ocean Engineering, 2010, 37(14-15): 1261-1272.
10.1016/S1001-6058(11)60315-6
* Project supported by of the National Marine Public Welfare Research Projects of China (Grant No. 201005002).
Biography: ZHAN Jie-min (1963-), Male, Ph. D., Professor
- 水动力学研究与进展 B辑的其它文章
- REVIEW OF SOME RESEARCHES ON NANO- AND SUBMICRON BROWNIAN PARTICLE-LADEN TURBULENT FLOW*
- EFFECT OF A PROPELLER AND GAS DIFFUSION ON BUBBLE NUCLEI DISTRIBUTION IN A LIQUID*
- APPLICATION OF QUADRATIC AND CUBIC TURBULENCE MODELS ON CAVITATING FLOWS AROUND SUBMERGED OBJECTS*
- THE HYDRODYNAMIC CHARACTERISTICS OF FREE VARIABLEPITCH VERTICAL AXIS TIDAL TURBINE*
- NUMERICAL PREDICTION OF SUBMARINE HYDRODYNAMIC COEFFICIENTS USING CFD SIMULATION*
- SIMULATION OF OIL-WATER TWO PHASE FLOW AND SEPARATION BEHAVIORS IN COMBINED T JUNCTIONS*

