齿轮啮合APDL精确建模与仿真

刘 越，张祖智，杜万里

（中国北方车辆研究所 车辆传动重点实验室，北京 100072）

0 引言

APDL是ANSYS参数化设计语言（ANSYS Parameter Design Language）的简称，是一种类似于FORTRAN的解释性语言。可以自动完成大部分图形用户界面（GUI）操作任务，甚至可以完成某些GUI无法实现的功能[1]。APDL语言是以*.txt文档的形式编写的，可由ANSYS直接运行。

圆柱齿轮传动是机械传动中最为常见的形式，齿轮设计的主要内容之一是强度设计。传统的国家标准校核仅能宏观的掌握齿轮的安全系数，在重载、高速、高可靠性和轻量化设计中，仅运用安全系数表达轮齿的受载特性是不够的，利用有限元仿真分析作为齿轮强度的校核方法，可以准确地掌握轮齿应力的分布特点和变化规律，是国家标准校核计算的有力补充，具有重要的意义。运用APDL程序可实现齿轮啮合有限元建模与仿真的参数化和自动化。

1 齿轮精确模型的建立

精确建立齿轮的三维实体模型是有限元分析结果准确性的基础，运用APDL建立齿轮的三维实体模型的关键是齿轮渐开线齿廓曲线和齿根过渡曲线的生成，这也是齿轮啮合有限元分析的重点研究部位。

1.1 渐开线齿廓曲线的生成

如图1所示，当直线L沿半径为rb的圆作纯滚动时，该直线上的任一点K的轨迹成为该圆的渐开线，轮齿的齿廓形状就是渐开线的一部分。

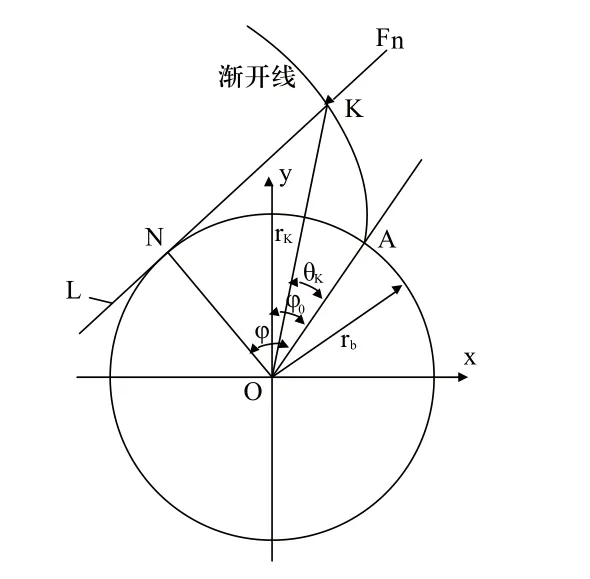
图1 渐开线的形状

直角坐标系中，已知渐开线的极角θK的始边OA与y轴的夹角φ0。

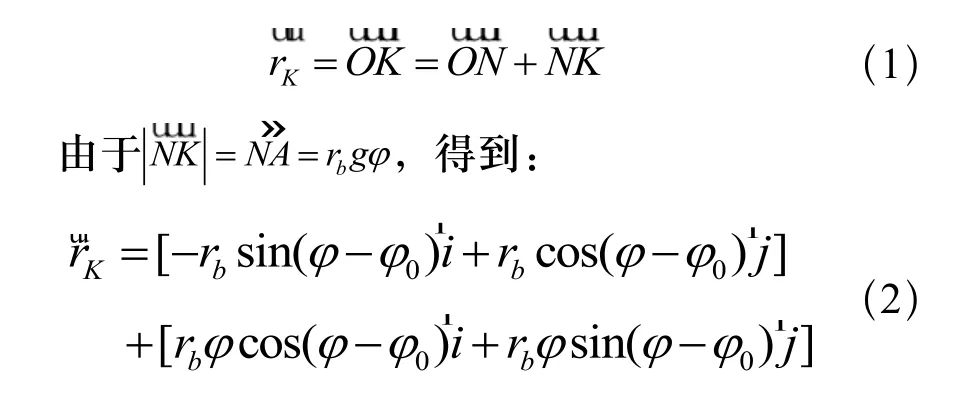
APDL程序中的齿轮建模取φ0= 0时的啮合状态，可得到直角坐标系下的渐开线方程：

渐开线的极坐标方程是：

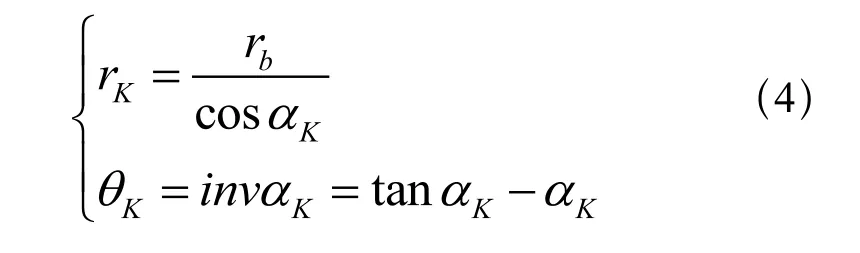
式中：rb为基圆半径；θK为渐开线K点的展角；αK为渐开线K点的压力角。

从渐开线方程可以看出，当基圆半径rb一定时，一个αK值对应一确定的rK和θK值，即确定了渐开线上一点坐标，设置取点步长φ，对得到的一系列关键点用光滑的样条曲线连接起来就形成了渐开线。

1.2 齿根过渡曲线的生成

研究表明[2]，齿根过渡曲线对齿根弯曲应力的影响是比较显著的。用齿条型刀具加工齿轮，相当于齿条与齿轮的啮合。被加工齿轮齿廓的渐开线部分由刀具切出。加工过程中，刀具加工节线与齿轮的加工节圆相切纯滚。如图2所示，直线nn是刀具圆角与过渡曲线接触点的公法线，α’是直线nn与刀具加工节线间的夹角。刀具的圆角加工出齿根过渡曲线，齿根过渡曲线的参数方程式：

以上各式中：d为分度圆直径； 为齿顶高系数；c为顶隙系数；m为齿轮模数；α为分度圆上的压力角；s为分度圆上的齿厚。

在参数方程中， 是变参数，在α ～ 90º范围内变化。对应于不同的 角，利用式（5）求出齿根过渡曲线上不同点的坐标。对得到的一系列关键点用光滑的样条曲线连接起来形成齿根过渡曲线。

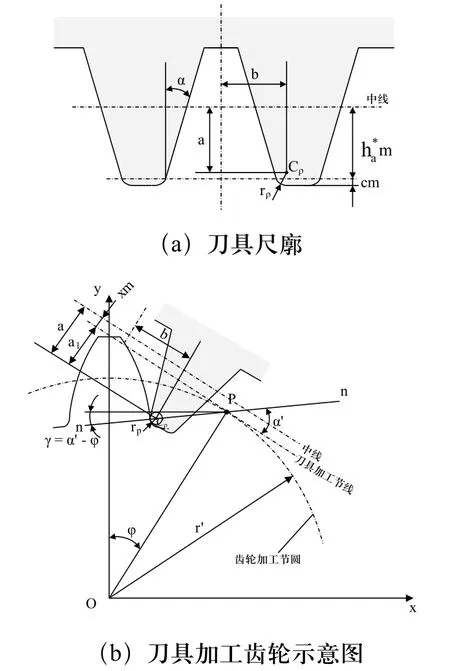
图2 刀具加工齿根过渡曲线

根据式（3） ～式 （5）推导出的齿廓渐开线和齿根过渡曲线计算式，在ANSYS中利用APDL编程求解出一系列关键点的坐标值并生成关键点。通过样条曲线联结关键点，生成部分齿廓及齿根过渡曲线，通过镜像、复制、旋转、布尔运算和拉伸等命令完成整个齿轮的建模。完成齿轮建模后，下一步的工作是实现齿轮的正确啮合，齿轮啮合的静力学分析应选取危险啮合位置，即单对齿啮合状态。将被动轮在x轴上平移中心距距离，主动轮旋转90°-θ1(θ1为主动轮分度圆啮合点处的展角 )，被动轮旋转 -(90° + θ2)(θ2为被动轮分度圆啮合点处的展角)。若重合度1≤ε <2时，危险啮合位置便是单齿啮合状态，如图3所示。

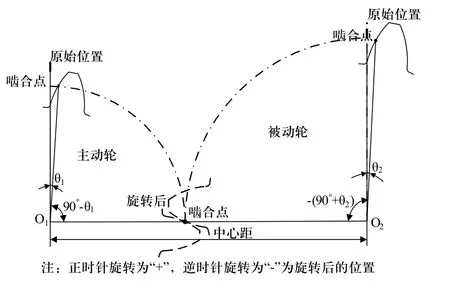
图3 齿轮啮合控制

运用APDL所建立的齿轮啮合三维实体模型如图4所示。

图4 齿轮啮合有限元分析模型

2 齿轮啮合有限元仿真

模型创建完成后，齿轮啮合有限元分析的步骤如图5所示。

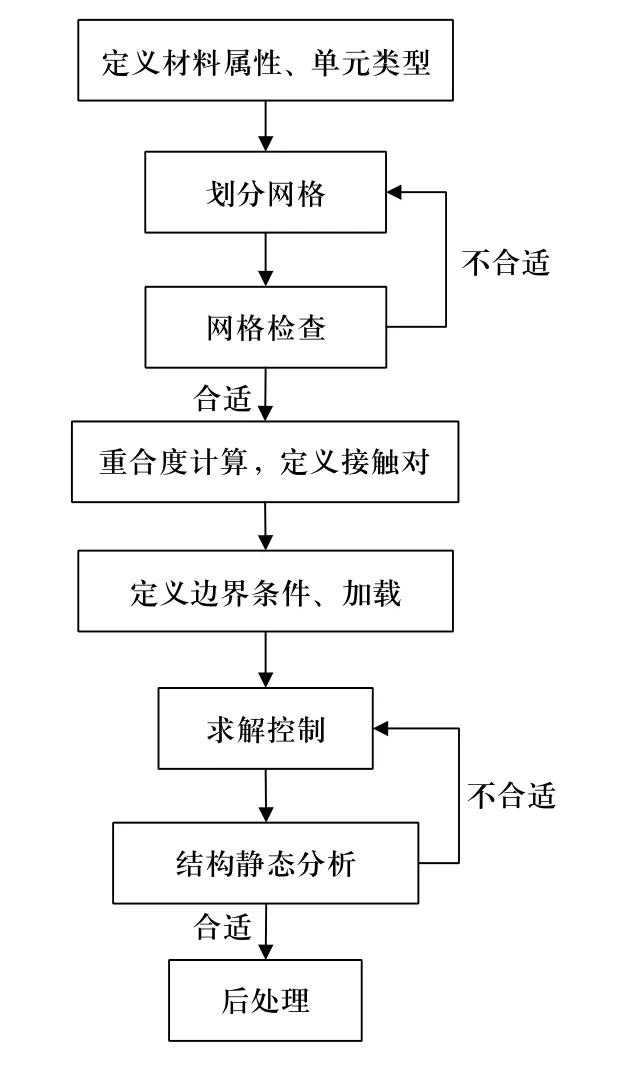
图5 齿轮啮合有限元分析步骤

网格划分是有限元分析前处理至关重要的一步，既影响计算的精度，又影响计算的速度。APDL程序设置的网格单元是SOLID185六面体实体单元，采用网格扫掠划分方式，对重点区域（轮齿部位）网格细化以保证计算结果的准确性，又使计算速度得到保证。网格划分后的模型如图6所示。接触对的数目依赖齿轮的重合度，程序根据用户在APDL对话框中输入的基本参数，计算齿轮对的重合度，并根据重合度的大小，自动识别、定义接触对（一般直齿轮重合度在1和2之间，但斜齿轮的重合度可能大于2）。当重合度ε ＞ 2时，危险状态时将会有两对齿啮合，需定义两对接触面。

图6 网格划分

图7 有限元分析结果

齿轮接触是典型的“柔体——柔体”的“面——面”接触问题。在非对称接触时，定义接触面和目标面遵循以下原则[3]：粗网格表面定义为目标面，细网格表面定义为接触面；材料刚度悬殊较大时，材料刚度大的一面为目标面；平直或凹面为目标面，凸面为接触面。程序中的两齿轮为对称接触，设主动轮为接触面，被动轮为目标面。接触单元选取TARGE170和CONTA174，接触算法采用Lagrange乘子法，并设置接触参数（接触刚度等）。

APDL程序通过以下方法对模型施加载荷：将被动轮的轮毂表面节点的所有自由度固定，将当前坐标系转换为柱坐标系，主动轮轮毂表面节点的节点坐标系按当前柱坐标系旋转，约束除主动轮表面节点绕中心转动的自由度外的两个自由度。同时将力矩转化为轮毂表面节点的均布切向力。

齿轮接触属于非线性问题，合理的控制时间步长可以减少求解收敛所需要的时间，因此采用自动时间步长特征，让程序自动选择足够小的时间步长。APDL程序中统一设置为50个平衡迭代次数，并且使用线性搜索命令。

APDL程序使用一般的后处理器（POST1）查看分析结果，主要包括位移、综合应力和接触应力等信息。分析结果如图7所示。

3 齿轮啮合有限元分析的APDL二次开发

APDL的宏是具有某种特殊功能的命令组合，可以当作ANSYS命令处理。通过对用户工具条的编写，用户可以很方便地使用宏命令。如图8所示。

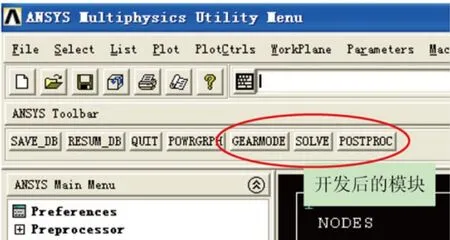
图8 用户工具条

创建的宏文件及其功能包括。

1）GearModel.mac：建立齿轮有限元分析模型的程序。可通过其交互界面输入齿轮的基本参数，包括模数、齿数、变位系数、压力角、螺旋角、齿顶高系数、顶隙系数、齿宽、齿轮轮毂直径、材料弹性模量和泊松比；

2）Solve.mac：求解计算模块程序。可通过其交互界面输入齿轮的载荷和边界条件，包括传动力矩、载荷系数和摩擦系数；

3）Postproc.mac：后处理程序。用户通过该模块查看仿真结果。

交互界面通过MULTOPRO和*CSET命令组合来实现，MULTOPRO命令的功能是构造一个多行提示对话框，该命令允许使用UIDL中的*CSET命令来产生提示，并为每个提示设定默认值。

APDL程序中定制多参数输入对话框的程序段如下：

MULTIPRO,'START',Prompt_Num

……

*CSET,1,3,mn,'NORMAL MODULUS',5.5!用户输入模数

*CSET,4,6,an,'NORMAL PRESS ANGLE(deg)',25 ！用户输入压力角（。）

*CSET,7,9,bita,'HELIX ANGLE(deg)',0！用户输入螺旋角（。）

*CSET,10,12,han,'NORMAL TOOTH ADDENDUM FACTOR',1 !用户输入齿顶高系数

*CSET,13,15,cn,'NORMAL TIP CLEARANCE FACTOR',0.2 !用户输入顶隙系数

*CSET,……

……

MULTIPRO,'END'

……

*IF,_BUTTON,EQ,1,THEN ！如果用户选择Cancel终止运行宏

/EOF

*ENDIF

用户点击用户工具条中的开发模块，调用相应的宏程序文件，在交互界面上输入相应的参数，进行建模、加载、计算，结束后可点击Postproc模块进行后处理操作。交互界面如图9所示。

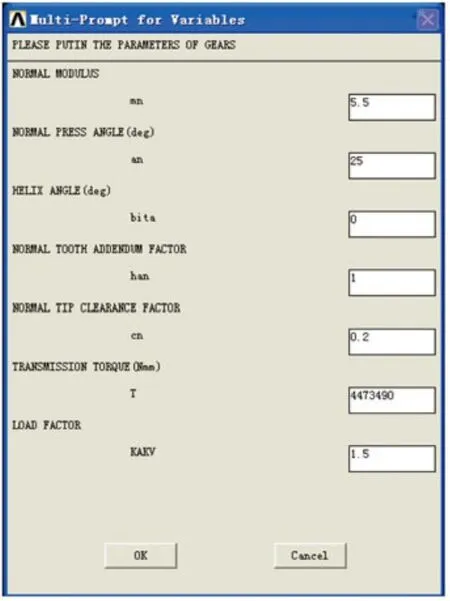
图9 交互界面

4 结论

运用APDL程序实现了齿轮啮合有限元分析的全过程，建立了参数化的分析模型和参数化的材料定义、自动化的网格划分与控制、自动化的载荷和边界条件定义以及自动化的后处理，用户通过交互界面直接与ANSYS求解器进行数据交换，与传统的GUI操作相比，大大提高了仿真效率，并且，减少了设计人员在仿真过程中对软件专业知识的依赖。

[1] 周宁. ANSYS APDL高级工程应用实例分析与二次开发[M]. 中国水利水电出版社, 2007.

[2] 吴继泽, 王统. 齿根过渡曲线与齿根应力[M]. 国防工业出版社, 1989.

[3] [美]Saeed Moaveni. 有限元分析—ANSYS理论与应用[M].电子工业出版社, 2008.