一种修正的灰色模型在交通量预测中的应用
杨 慧,王 峥
(郑州铁路职业技术学院,河南 郑州 450052)
灰色系统理论中应用最广泛的GM(1,1)模型,由于其所需样本数据较少,运算方便,短期预测精度较高等优点,已成功地应用于社会、经济等各个领域[1-9]。但对于既有总体变化趋势又有波动性的数据序列,GM(1,1)模型预测精度不高[3-6]。为了提高GM(1,1)模型的预测精度,一些学者在这方面做了许多工作,提出了一些改进的方法[1、2、5、6],如残差修正模型、遗传算法等。残差GM(1,1)模型要求残差尾段必须有相同的符号,对于既有总体变化趋势又有波动性的数据序列,这个条件很难得到满足。遗传算法具有模仿多种函数的能力,特别适合对GM(1,1)模型进行残差修正,但遗传算法需要有足够多的学习样本来训练这个网络,当样本数量较少时,预测的精度也不太理想。
在没有安装检测器的路段,交通流量数据的获得只能靠人工计数来完成,不可能获得大量的数据。陈淑艳、陈家胜[2]将GM(1,1)模型与遗传算法结合起来应用于交通量的预测,取得了比孙燕、陈森发[3]等人更好的结果,但受样本数量较少的限制,预测的精度仍不太理想。对既有总体变化趋势又有波动性的数据序列,笔者先用GM(1,1)模型筛选出趋势成份,然后对实际值与拟合值的差值构成的残差序列,作Fourier变换,提取出周期波动成份,最后将二者叠加,进行残差修正,将该方法应用于实际,效果比较理想。
1GM(1,1)模型的建立
1.1 传统的GM(1,1)模型
设 X(0)=x(0)(1),x(0)(2),…,x(0)(n(
))为非负的原始数据序列,其1-AGO为:
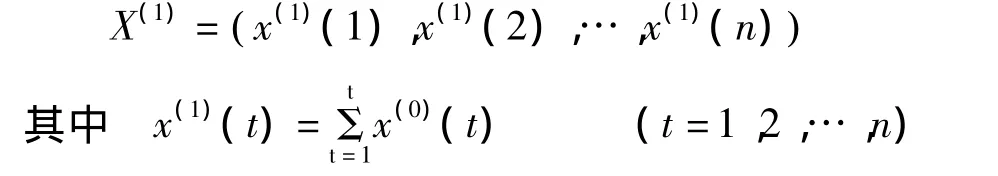
X(1)的近邻生值生成序列为

若原始数据序列X(0)满足:

则称X(0)为准光滑序列。
可以证明[1],若X(0)为准光滑序列,则其一阶累加生成序列X(1)具有准指数规律,可对X(1)建立GM(1,1)模型:

以x(1)(t)|t=1=x(1)(1)为初始条件的解为
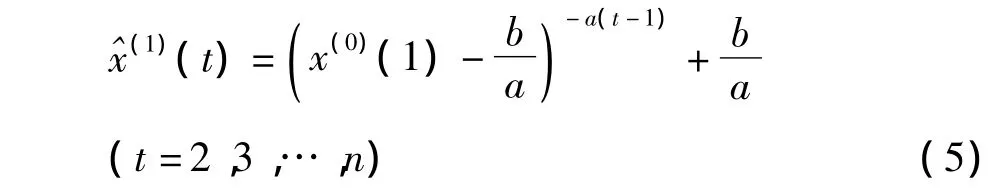
对 ^X(1)累减还原求出X(0)的模拟值

1.2GM(1,1)模型的改进
文献[7]证明了利用(7)式代替(1)式可以摆脱因背景值构造不当而产生的系统误差。
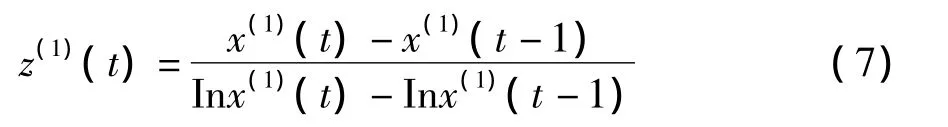
(7)式中当x(1)(t)=x(1)(t-1)时,规定 z(1)(t)=x(1)(t)。
(5)式是基于拟合曲线一定经过第一个数据点(1,x(1)(1))而得到的,我们知道,由最小二乘法得到的拟合曲线,理论上不一定通过任何一个点(m,x(1)(m))。因此,为进一步优化GM(1,1)模型,微分方程(3)的通解

中的任意常数c可根据X(1)与其模拟值 ^X(1)偏差平方和为最小的原则确定为[1]
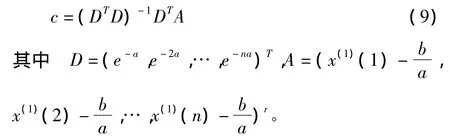

累减还原得X(0)的模拟值为

2 GM(1,1)残差尾段波动变化趋势的修正
交通量受多种因素的影响,具有很大的随机性,其时间序列往往含有多个周期波,这些周期波的波长和振幅又各不相同。本文采用傅立叶级数,将波动序列成份看成是各种周期波形叠加的结果。
设 X(0)=x(0)(1),x(0)(2),…,x(0)(n())的残差序列为

ε(t)等于 m 个波形在 t(t=1,2,…,n)时刻取值的总和:

应用最小二乘法,可得傅立叶系数[10]

在实际工作中,为简化计算,并不要求所有的周期分量都加入预测方程,而是寻求影响最大者,即振幅最大者。振幅的计算公式为
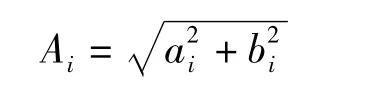
将趋势成份与波动成份叠加,得原始数据序列的模拟值

3 应用实例
无检测器的路段获得的交通量数据有限,故将该模型用于无检测器路段的交通量预测。为便于对比,使用文献[2]提供一组交通量数据序列
(11,10,11,13,15,16,16,15)
前6个数据用于建模,后2个数据用于模型检验。
经计算得 ρ(3)≈0.524,ρ(4)≈0.406,ρ(5)≈0.3333,ρ(6)≈0.2667,可以看出在 t>3 满足准光滑条件。建立GM模型为

利用该式可求出趋势模拟值,计算实测值与模拟值的差,得残差序列(0,-1.07342,-0.86,0.299,1.3984,1.43334),经计算得波动成份的回归方程为
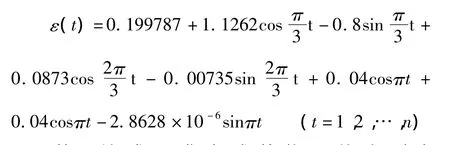
利用该式可求出残差修正值序列为(-0.20674,-1.2401,-1.0658,0.1328,1.19165,0.26664,-0.20673,-1.24),将趋势成份的模拟值与波动成份的模拟值叠加,即可得到拟合值和预测值,结果见表1。可以看出,本模型的预测精度略高于文献[2]。

表1 预测结果对比表
4 结语
对于既有趋势增长成份,又有波动成份的数据序列,若数据波动幅度比较小,可以应用该模型进行模拟,若波动幅度比较大,则需要先对原始数据进行变换,进行平稳化处理。
[1]刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2004,125 -209.
[2]陈淑燕,陈家胜.一种改进的灰色模型在交通量预测中的应用[J].公路交通科技,2004,21(2):80 -83.
[3]孙燕等.灰色系统理论在无监测器交叉口交通量预测中的应用[J].东南大学学报,2002,32(2):256 -258.
[4]李留藏,许闻天.灰色系统 GM(1,1)模型的讨论[J].数学的实践与认识,1993(1):15-22.
[5]Deng Julong.A novel GM(1,1)model for non - equigap series[J].The Journal of Grey System,1997,9(2):111 -116
[6]Kuo Ching Ying,Ching Tong Liao.Fourier modified non -equigap GM(1,1)[J].The Journal of Grey System,2000,12(2):139-142.
[7]罗党,刘思峰,党耀国.灰色模型 GM(1,1)优化[J].中国工程科学,2003,5(8):50 -53.
[8]高曙.基于残差变化趋势的GM(1,1)修正模型的算法实现与应用[J].武汉理工大学学报,2003,25(6):17 -19.
[9]孙才志,潘俊.修正的灰色模型在水文时间序列分析中的应用[J].工程勘察,2000(3):25-26.
[10]李铁映,张昕.预测决策方法[M].沈阳:辽宁科学技术出版社,1984:407-416.

