基于多元线性回归模型的中国人口老龄化影响因素研究
陈仁爱 刘 婷 冯贤财 吕云凯 陈佳君
(温州医学院 浙江 温州 325035)
0 引言
人口老龄化是指总人口中因年轻人口数量减少、年长人口数量增加而导致的老年人口比例相应增长的动态。 我国从1999 年开始就进入了老龄化社会[1],第六次全国人口普查显示,65 岁及以上人口占8.87%,比2000 年人口普查上升1.91个百分点。 据社科院权威发布,2011 年以后的30 年里,中国人口老龄化将呈现加速发展态势,到2030 年,中国65 岁以上人口占比将超过日本,成为全球人口老龄化程度最高的国家。 由于我国人口基数大,人均收入水平还很低,有可能是使老龄化带来的危机放大化,导致“未富先老”[2],所以对我国老龄化的影响因素进行研究并加以干预显得尤为重要。
1 数据来源与研究方法
人口老龄化最直接因素是出生率和死亡率,出生率下降会导致人口年龄金字塔的底部变窄即相对老龄化,而死亡率下降则会导致金字塔的顶部增宽即绝对老龄化[3]。 但仅仅通过出生率和死亡率来研究人口老龄化太过宏观,因为这两个因素本身是有众多其他间接因素所决定的,因而应从出生率和死亡率这两个方面出发,从微观角度对影响人口老龄化的间接影响因素进行分析研究。 本文根据数据的可获得性、借鉴国内外文献并结合我国国情,选取了5 个能够影响出生率和死亡率的因素进行定量分析:
(1)人均国内生产总值X1(元)。 该指标是衡量各国人民生活水平的标准。 人均国内生产总值越高,说明人民的生活水平越好,人的寿命就得到延长,我国解放前后的国情比较就是很好的例证。
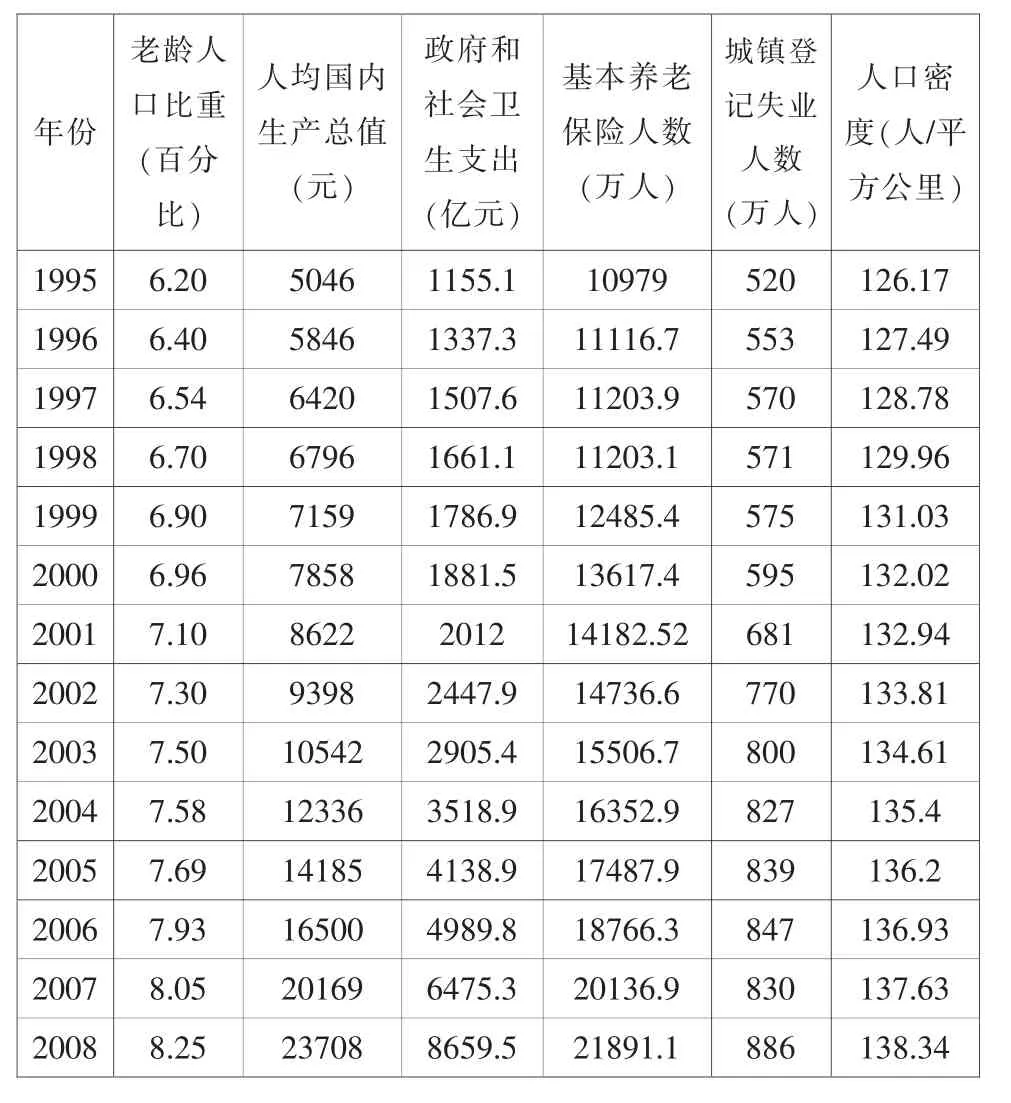
表1
(2)政府和社会卫生支出X2(亿元)。 该指标反映包括政府在内的社会各界对卫生事业的资金投入。 投入的资金越多,则公众能享受到的服务和保障力度越大,就越有益于人的寿命的延长。
(3)城镇基本养老保险人数X3(万人)。 该指标反映养老保险的普及率。 养老保险是为了保障老年人的基本生活需求,为其提供可靠的生活来源。
(4)城镇登记失业人数X4(万人)。 该指标反映一个国家或地区的就业情况。 失业人数越多,说明人们的就业压力就越大,影响人们的生育意愿,导致出生率降低。
(5)人口密度X5(人/平方米)。 该指标反映单位国土面积上居住的人口数,是描述人口密集程度的指标。 人口密度大时,由于空间与自然资源的限制,势必会导致出生率下降[4]。
根据我们选取好的指标,从历年的《中国统计年鉴》中得到了以下数据(见表1)。
2 人口老龄化与影响因素的回归分析
2.1 模型的建立
人口老龄化受多个因素影响,所以设人口老龄化比重为因变量Y,5 个影响因素(X1~X5)为自变量,准备建立多元线性回归模型:
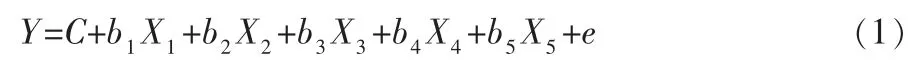
其中,C 为常数项,b1~b5为因变量Y 对自变量X1~X5的回归系数,e 为残差。
接着,作5 个影响因素(X1~X5)与人口老龄化比重(Y)的散点图。
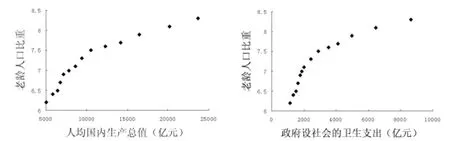
图1 人口老龄化比重与影响因素的散点图
由散点图得知,Y 与X3、X4、X5呈线性相关, 而与X1、X2线性相关性较差(如图1),通过SPSS 曲线拟合得知,自变量X1、X2与因变量Y 呈对数关系, 所以需对这2 个变量进行对数转换, 分别得到新的自变量X6=logX1,X7=logX2, 然后对(1)式进行修正,得到新的模型:
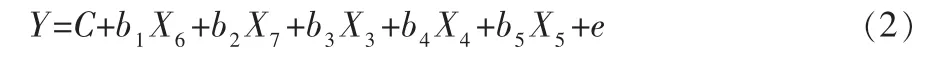
再用SPSS 进行逐步法(Stepwise)进行分析,得出的多元线性回归模型是:

2.2 模型检验结果分析
(1)模型拟合度与Durbin-Watson 值检验
根据SPSS 的运行结果, 表2 表明模型的相关系数R 为0.999,决定系数R2为0.998,校正的决定系数为0.997,即自变量可以解释因变量的变异的99.7%, 说明模型的拟合结果较好。 而模型的Durbin-Watson 值为2.391,接近于2,说明残差间相互独立。
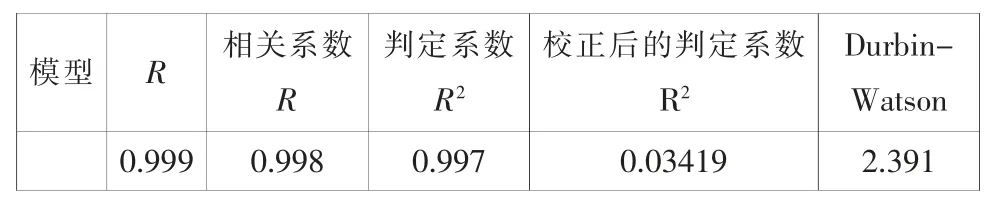
表2 模型拟合度与Durbin-Watson 值检验
(2)模型的统计学意义检验
根据SPSS 运行结果中的标准方差分析表得知, 回归模型的F 值为2268,P<0.01,说明模型有统计学意义。
(3)各变量的显著性检验
为了确定哪些自变量对因变量的影响显著,还需进一步对模型中的回归系数进行检验。 表3 中变量X5、X7和常数的非标准化回归系数的P 值均小于0.05,通过t 检验,说明模型中的自变量可以很好的解释因变量的变异。 而另外变量X1、X3、X4的t 检验未通过, 说明这3 个自变量对因变量的影响不显著,故不能存在于模型中。
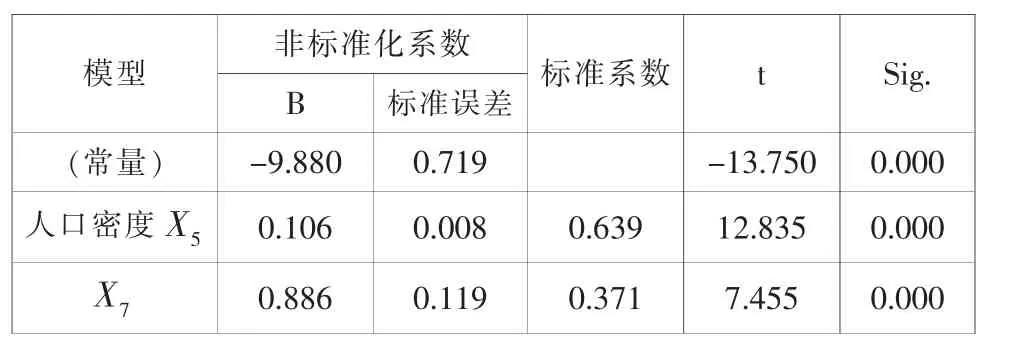
表3 回归模型系数
(4)残差分析
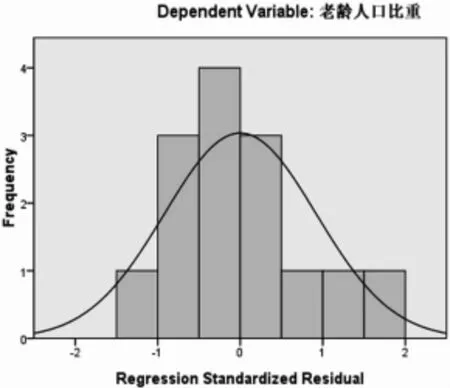
图2 残差分布直方图
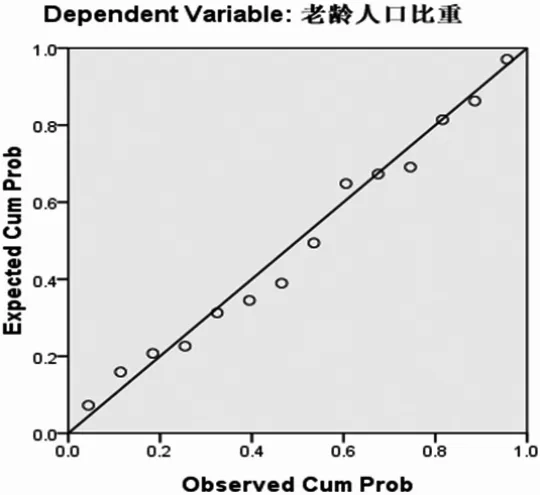
图3 PP 概率图
图2 为残差分布的直方图,直方图上残差分布大致呈正太分布,不存在极端值。 图3 为因变量累计概率和模型预测值累计概率间的正太PP 图,残差散点呈直线趋势,符合正太分布,也不存在极端值。
3 模型的应用价值与实际意义
前面已经对模型的合理性进行了理论上的分析检验,接下来要用模型来预测2009 年的老龄人口比重, 并与年鉴里的实际值比较,以检验模型的预测能力和实际应用价值。
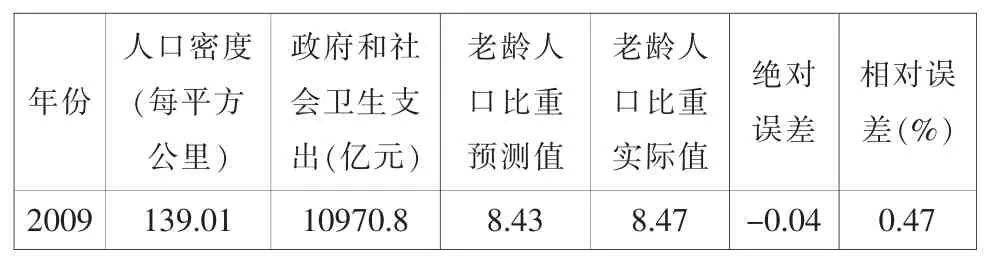
表4 2009 年老龄人口比重预测值与实际值比较
由表4 可见,模型的预测值与实际值几乎相等,说明模型具有很好的预测价值,可以应用于今后我国人口老龄化程度的预测。 有学者用GM(1,1)灰色预测模型对我国的人口老龄化趋势进行预测, 其预测的2009 年老龄人口占总人口的百分比为8.31%[5],可见本模型的预测结果更加准确。 这是因为灰色预测模型适用于统计数据少、 时间序列短的情况下,且不能够反映自变量与因变量的具体关系,因而当实际中某个自变量出现极端值时,就会导致预测的结果与实际值偏差较大。 而本模型在原始数据相对较多的情况下,通过对多个自变量的筛选得出多元线性回归模型,显然比GM(1,1)灰色模型相对笼统的预测更能准确预测实际情况。
同时,从模型中可以看出,政府社会卫生支出和人口密度是影响我国老龄人口比重最重要的影响因素,且两者对人口老龄化的影响都是正向的。2009 年我国个人卫生支出占卫生总费用降至37.5%,但仍然远高于欧美发达国家,依然给居民带来较重的经济负担[6],因而未来一段时间内,我国的政府社会卫生支出仍然会持续快速增长,人均寿命将会进一步提高。 而对于人口密度,自20 世纪80 年代以来,计划生育的实施很好控制住了人口密度过快增长,在控制人口老龄化方面起到了积极作用,因而今后很长一段时间计划生育依然会作为国策来实行,但不能一味地只控制人口数量而忽略世代更替,这反而会加重人口老龄化程度。
4 结语
人口老龄化虽然不可避免,但可以通过采取有效措施延缓其进程[7],而这些措施可以通过控制人口老龄化的影响因素来实现。 本文选取了5 个影响因素指标建立了我国人口老龄化的多元线性回归模型, 模型具有较高的预测准确度,并能很好地用实际情况加以解释,可以用来指导有关部门作好充分地准备,认清老龄化的危机,完善社会保障制度,同时也应当从危机中寻找契机,发展老龄化产业,充分利用老龄人力资源,使我国社会经济和谐稳定发展。
[1]原新,刘士杰.1982-2007 年我国人口老龄化原因的人口学因素分解[J].学海,2009(4):140-145.
[2]刘思敏.中国人口老龄化现状及其对策分析[J].理论探讨,2011(12):298-300.
[3]朱静芬.少子老龄化背景下我国商业保险的发展机遇[J].重庆科技学院院报,2011(16):73-76.
[4]任强,沃夫冈.人口密度与生育率:一项探索性分析[J].中国人口科学,2003(5):1-10.
[5]时丽娜,黄汉明,李小勇,等.基于等维灰数递补动态模型的人口老龄化趋势预测[J].鲁东大学学报,2009,25(4):315-317.
[6]李永胜.老龄人口统计分析[J].老龄人口,1989(3):35-41.
[7]徐颖科,张志超.中国个人卫生支出与经济增长协整关系研究[J].中央财经大学学报,2010(3):61-65.
——与非适应性回归分析的比较

