光纤可调F－P滤波器频率响应特性的实验研究＊

王 浩，余有龙，王雪微

（合肥工业大学 仪器科学与光电工程学院，安徽 合肥 230009）

引 言

光纤光栅（fiber Bragg grating，FBG）传感器具有质量轻、灵敏度高、抗干扰、易于复用成网等优点，而广受关注［1－2］。该传感器的信号采用波长编码，现有的解调技术主要有干涉法［3］、滤波法［4］和色散法［5］。其中可调Fabry－Perot（F－P）滤波解调技术，是通过波长扫描，确定FBG反射光透过滤波器后峰值对应的波长（即布喇格波长）所对应的驱动电压，利用两者的对应关系，反演算出传感量的变化［6］。现有的可调滤波器均采用压电陶瓷（PZT）驱动，PZT的蠕变以及迟滞效应会造成滤波器透过波长与驱动电压间呈非线性变化关系［7］，同时PZT驱动频率的变化也会使滤波器透射波长发生改变，从而会影响解调精度。针对PZT非线性对解调精度的影响，有学者提出了多项式拟合［8］、参考光栅［9］、F－P标准具［10］等方法加以改进。而对于PZT频率响应特性（简称频响特性）对滤波解调结果的影响至今尚未见报道。

现借助可调光纤F－P滤波器对固定的激光输出进行波长扫描，并改变滤波器的驱动频率，通过观测输出脉冲，获得可调滤波器频响特性的实验结果。

1 原 理

根据多光束干涉原理，F－P滤波器的透射率［11］

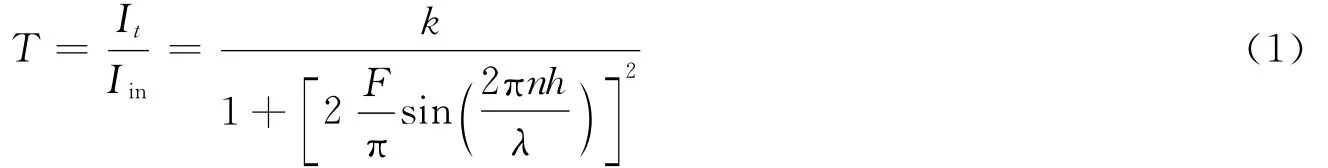
式（1）中，It和Iin分别是滤波器的透射和入射光强，h为腔长，λ为真空中光波长，n为腔内介质的折射率，k为反射膜的插入损耗，无损耗时为精细度，R为端面反射率。

平行光束垂直入射到全光纤可调F－P滤波器时，光在腔中往返光程Δ满足下述等式时，T取得最大值，即

式（2）中，m为干涉条纹的级次。对于特定的n和h，会有不同级次的分立波长输出，确定的级次m有对应的波长λm，此时

可调F－P滤波器中，腔长h是由PZT驱动，而PZT又受交变电压V（t）控制，这样h就随时间的变化而变化［12］，将腔长随时间的变化量表示为D（V（t））。根据压电陶瓷频率特性，PZT伸长量不仅与驱动电压大小有关，而且受到驱动频率的影响［13－14］，引入变量频率f，滤波器腔长变化的量可表述为

式（4）中，h0为初始腔长。将h（t）代入式（3），得

式（5）反应了滤波器的透过波长与压电陶瓷驱动电压大小和频率之间的关系，当驱动电压的大小或者频率改变的时候，滤波器的透过波长均会受到影响。因此，利用可调F－P滤波器对光纤光栅传感信号进行解调时，必须考虑驱动频率对解调结果的影响。

2 实验结果和分析

F－P滤波器的频率响应特性测试装置如图1所示，可调激光器输出波长为λ的单色光经衰减器后进入受锯齿波电压信号驱动的可调F－P滤波器，其输出经光电转换后放大，利用多路数据采集卡，对放大后的信号以及PZT驱动信号分别采集后输入电脑，借助LabVIEW软件平台，实时显示透过波长的位置和对应的驱动电压。

所用可调激光器的波长调节范围是1 500～1 630nm，波长分辨力1pm。可调F－P滤波器在1 550nm通信窗口的自由光谱程（FSR）为94nm，带宽为90.6pm，一个FSR调节电压18V。可调滤波器受锯齿波电压信号驱动，对光源输出波长进行周期性扫描。当滤波器透过波长与激光输出波长一致时，探测器输出达到最大值。对采集到的信号进行拟合、寻峰，拟合曲线的峰值对应于激光器输出波长。图2为时域内峰值以及驱动电压变化情况。试验中，激光器输出功率为0.02mW，锯齿波驱动电压信号的峰峰值和占空比分别为18V和为0%。

保持激光输出功率为0.02mW不变，在1 510～1 575nm范围内，每隔5nm依次调节激光输出波长，对于每一输出波长，扫描滤波后，在LabVIEW程序面板中读出峰值波长对应的驱动电压，得到如图3所示的实验关系。改变驱动频率，分别选取1Hz、10Hz、100Hz和200Hz，所得结果示于图3。

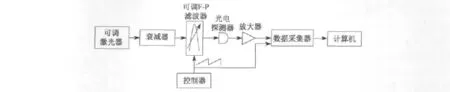
图1 系统原理图Fig.1 System diagram

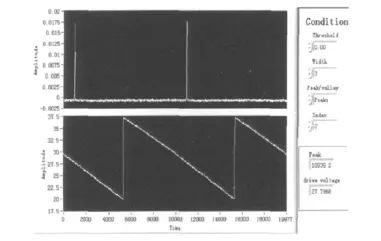
图2 LabVIEW程序面板Fig.2 LabVIEW program

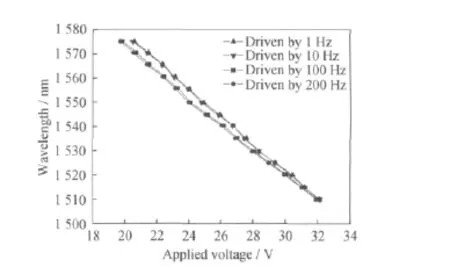
图3 在不同驱动频率下测得的滤波器波长－电压曲线Fig.3 Relationship between wavelength and applied voltage for different frequencies

从图3可以看出，F－P滤波器的透射波长与驱动电压间的关系明显受到驱动频率的影响，随着频率的增加，同一电压下F－P滤波器的透射波长会减小。这是因为PZT是由压电晶体组成，而压电晶体是各向异性的电介质，电介质在电场作用下会产生极化。当驱动电压的频率升高时，存在的极化弛豫将导致极化强度和电位移出现滞后。频率越高，滞后现象越明显，从而导致频率不同时，同一电压所对应压电陶瓷伸长量不相等［15］。

为了更好地说明滤波器透射波长随驱动频率的变化关系，排除掉所采集的两路信号经过距离不一样等原因产生的驱动电压和透射波长之间相位延迟的影响，现将所测得的曲线拟合成线性直线，只考量拟合所得到的直线的斜率。通过拟合所得到四条直线的斜率见表1。

表1中各频率所对应的斜率有单调递减的趋势。10Hz、100Hz和200Hz的斜率与1Hz时分别相差0.69%，5.10%，6.49%。对于依靠驱动电压与输出波长关系来解调光栅波长改变的解调仪，如果忽略这种频率带来差别，在改变解调频率的情况下，会使测量结果产生较大的误差。

对不同频率的曲线分别进行二次多项式拟合，用拟合出来的曲线代表不同频率下可调F－P滤波器透射波长与驱动电压的关系，可以减小频率改变对解调系统精度的影响。对上述曲线拟合后所得到的二次曲线与实际数据的相关系数分别是R1＝0.999 55；R10＝0.999 61；R100＝0.999 49；R200＝0.999 77。各拟合曲线表达式如下：

表1 拟合斜率Tab.1 The slope of fitting

以1 550nm波长的光为例，在1Hz、10Hz、100Hz和200Hz分别采集到的驱动电压是24.954 5V、24.873 5V、24.273 2V和24.129 7V。如果忽略可调滤波器频率特性，均以1Hz情况下驱动信号与透射波长的拟合曲线作为解调参考，上述电压所对应的波长分别为1 550.027 3nm、1 550.490 3nm、1 553.931 2nm、1 554.756 2nm，误差为0.027 3nm、0.490 3nm、3.931 2nm、4.756 2nm。而用对应各频率的拟合曲线所得结果为1 550.027 3nm、1 550.051 9nm、1 550.098 7nm、1 549.957 5nm，误差分别是0.027 3nm、0.051 9nm、0.098 7nm、0.042 5nm，相对忽略频率特性，10Hz、100Hz和200Hz情况下的误差分别减少了89.4%、97.5%、99.1%。如果采用参考波长结合多项式拟合的方法，可以实现不同频率下解调系统的实时标定，进一步提高系统的解调精度。

3 结 论

通过数据采集和基于LabVIEW的虚拟仪器，测试了光纤可调F－P滤波器在不同驱动频率下的响应。通过对比实验所获得的1Hz、10Hz、100Hz和200Hz下可调F－P滤波器驱动电压与透射波长的响应，观察到随着驱动频率的增加，同一电压对应滤波器的透过波长将减小，并解释了其原因。分析了忽略驱动信号频率与透射波长特性带来的解调误差，并采用二次多项式拟合对每个频率下的响应曲线进行拟合。当采用各自频率拟合曲线解调时，10Hz、100Hz和200Hz的波长解调误差分别减少了89.4%、97.5%、99.1%。通过对光纤可调F－P滤波器频率响应的实验研究，有利于进一步了解驱动频率对滤波器的影响，可以提高FBG传感系统滤波解调的精度。

［1］MAJUMDER M，GANGOPADHYAY T，CHAKRABORTY A K，et al.Fiber Bragg gratings in structural health monitoring－Present status and applications［J］.Sensors and Actuators A：Physical，2008，147：150－164.

［2］朱小平，吴晓冬，陈 军.基于DWDM 和LabVIEW 的新型光纤光栅传感技术［J］.光学仪器，2004，26（5）：21－25.

［3］KERSEY A D，BERKOFF T A，MOREY W W.Fiber－optic Bragg grating strain sensor with drift－compensated high－resolution interferometric wavelength－shift detection［J］.Optics Letters，1993，18（1）：72－74.

［4］KERSEY A D，BERKOFF T A，MOREY W W.Multiplexed fiber Bragg grating strain－sensor system with a fiber Fabry－Perot wavelength filter［J］.Optics Letters，1993，18（16）：1370－1372.

［5］JAMES S W，DOCKNEY M，TATAM R P.Photorefractive volume holographic demodulation of in－fiber Bragg grating sensors［J］.IEEE Photonics Technology Letter，1996，8（5）：664－666.

［6］余有龙，谭华耀，锺永康.基于可调F－P滤波器的光纤光栅传感器阵列查询技术［J］.中国激光，2000，27（12）：1103－1106.

［7］余有龙，谭玲，邹李刚等.用光纤光栅传感器研究压电陶瓷的特性［J］.光子学报，2011，40（7）：994－997.

［8］LIU K，JING W C，LIU T G，et al.Design and nonlinearity compensation of Fabry－Perot type tunable optical filters for dynamic strain sensing systems［J］.Optoelectronics Letters，2008，4（4）：248－252.

［9］NING Y N，MELDRUM A，SHI W J，et al.Bragg grating sensing instrument using a tunable Fabry－Perot filter to detect wavelength variations［J］.Meas Sci Technol，1998，9（4）：599－606.

［10］梁 霄，刘铁根，刘 琨，等.一种可调谐光滤波器非线性实时标定方法研究［J］.中国激光，2010，37（6）：1145－1149.

［11］江 毅，唐才杰.光纤Fabry－Perot干涉仪原理及应用［M］.北京：国防工业出版社，2009：9－95.

［12］LIU K，JING W，PENG G D，et al.Investigation of PZT driven tunable optical filter nonlinearity using FBG optical fiber sensing system［J］.Optics Communications，2008，281：3286－3290.

［13］陈 超，何玉琳，章海军.压电陶瓷微纳米伸缩测试系统［J］.光学仪器，2007，29（2）：27－30.

［14］肖 嘉，赵建伟，田 莳.压电陶瓷驱动器三角波频率特性［J］.压电与声光，2003，25（3）：203－206.

［15］吴一辉，杨宜民，王立鼎.压电定位元件的非线性及其线性化控制原理［J］.功能材料与器件学报，1996，2（3）：166－171.