渐变焦眼镜片的设计方法研究*
倪瑞遥,陈家璧,庄松林
(上海理工大学 光电信息与计算机工程学院,上海 200093)
引 言
随着年龄的增长,人们眼睛的调焦能力逐渐减弱,成为通俗意义上的老花眼。传统的矫正方法是佩戴正光焦度镜片即老花镜,但这种方法不能兼顾矫正近视眼。人们需要一副兼顾远近的眼镜,由此单光镜逐渐发展成双光镜和三光镜,但由于其观察中距离效果不佳,每个区域的聚焦范围有限,不能获得全程的连续视觉,在分界线处存在“像跳”的现象,给使用者带来不便。在这种需求下,渐变焦眼镜应运而生。渐变焦镜片是一种光焦度由上而下逐渐增加的镜片,只用一块镜片就可以提供连续的由远而近都较清晰的视觉。
1907年美国人Owen Aves首次提出渐变焦镜片的构思[1]:镜片由前后两个曲面构成,将前面设计成球面形式,将后面设计为垂直(子午线)方向为弹道曲线状的曲面形式。1910年Henry Orford Gowlland提出了使用非球面技术解决镜片渐进的思想,但由于技术限制,并没有获得实际应用。1920年,伯莱恩和考涅特提出了新曲面的概念,即镜片的两个曲面由弯曲度自上而下逐渐加大的镜面构成,从而实现镜度自上而下逐渐增加的目的[2-3]。但是,这两种镜片有同样的明显缺陷:像差太大,超出人眼所能承受的限度,无法佩戴使用。
法国依视路公司的光学工程师Bernard Maitenaz于1958年获得了突破性进展,第一次描述了这种镜片的加工方法,同年,依视路公司研制出真正适合临床佩戴的第一副渐变焦眼镜,1959年依视路正式命名这种镜片为Varilux I,并将其投入市场一举获得成功[4]。
而后,1972年依视路又推出了第二代的生理性渐进镜片,相比第一代着重提高了中距离的视效,强调视觉均衡,而第三代的多样化设计渐进镜片则寻找了多种加光度的合理曲面,以解决不同年龄的老视者的需求,1993年推出了第四代以使佩戴者得到更接近正常生理状态的舒适型渐进镜片,2000年已经推出第五代全景超视渐进镜片以期佩戴者得到更完美的空间视觉和知觉[5-6]。
正是渐变焦眼镜市场有很好的发展前景,所以国内外很多学者都进行了相关的研究工作,包括用哈特曼传感器进行一些测量工作[7]、比较各种渐变焦镜片的设计方法[8]和对渐变焦子午线的相关研究[9]。但是大多学者都只是进行了一些分析工作,关于渐变焦镜片的详细设计方法和研制报告并不多见。文中介绍了渐变焦眼镜片的结构和原理,给出其子午线上光焦度分布和面型的设计方法,并分析子午线光焦度分布设计在渐变焦镜片研制中的作用。
1 渐变焦眼镜片的结构
渐变焦镜片可以近似看成由若干个视球在垂直方向连接而成(图1)。当然,渐变焦镜片结构是任意点的光焦度平滑连接而成的曲面结构,正是这一连续的曲面结构,实现了镜片上的光焦度的渐进变化,使渐变焦镜片佩戴者的视野不再被割断而是连续的,从而佩戴者在视觉范围内可以得到自然的视觉生理状态。
渐变焦眼镜片一般分为视远区、视近区、中间过渡区和像散区4个区域,如图2所示。视远区A为位于渐变焦镜片上半部分的宽阔区域,在人眼处于放松平视状态下矫正视远能力,提供清晰、宽阔的视野。视近区C对于大多数渐变焦镜片来说位于视远参考圈中心下方约10~18mm,具体位置因渐变焦镜片使用类型、设计方法以及校正老视程度、人眼瞳距和用眼习惯等的不同而有相应的差异。渐变区B是连接视远区和视近区的中间区域,也是渐变焦镜片设计的核心,为渐变焦镜片区别于双光镜的主要特征区域。根据不同的设计样式,渐变区可以是线性变化,或呈其他函数形式变化。文中的设计方法是后者,这样的设计可以使渐变镜的视近区位置较高、宽度较大,改善视觉效果好。
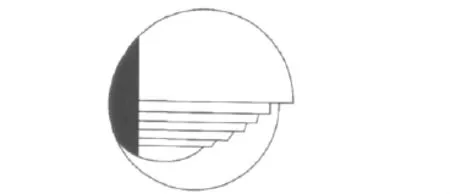
图1 镜片矢状剖面与多球面关系Fig.1 Relation of sagittal section to spherical
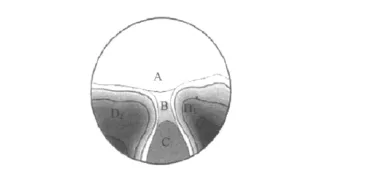
图2 渐变焦眼镜的分区示意图Fig.2 Areas of progressive power spectacles
像散区D1和D2为镜片两侧存在像差的区域,由于镜片表面曲率变化导致的像差,主要为散光和棱镜像差,在一定程度上会干扰视觉、产生视觉模糊或变形,影响佩戴者对镜片的适应。这些像差是渐变焦眼镜与生俱来的,它的存在无论是从设计上还是从工艺上都无法完全消除。镜片两侧的像差始终会造成视物变形,尤其当眼睛由渐变区向旁边看时更甚。
2 渐变焦眼镜片的设计方法
2.1 子午线设计
渐变焦眼镜片为一个平凹(凸)薄透镜,其前表面为平面(当需要将前表面制作成凸面时则另一面为平面)。如图3所示为平凸薄透镜,定义一个右手直角坐标系o-xyz,坐标面xoy和镜片后表面相切于几何中心点o,x轴竖直向下,y轴垂直纸面向外,z轴指向人眼,镜片的前表面为平面,对于光焦度没有贡献,不予考虑。若镜片材料的折射率为n,则渐变面上任意点的光焦度等于此点处的曲率和镜片与空气折射率之差(n-1)的乘积。
考虑子午线的情况,从视远区参考点F到视近区参考点N曲率半径逐渐变化。设F点相对o点沿x轴向上偏移长度为L,F,N 之间的距离为h,子午线MM′上任一点Q(u,0,z)的曲率和其x轴坐标值u{u∈[-L,-L+h]}的关系一般可以由下面的 N 阶多项式[10-12]表示:
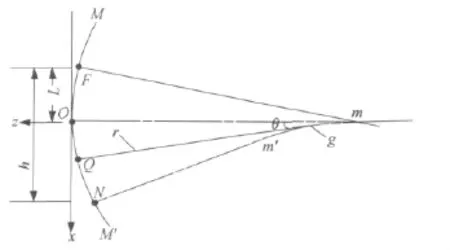
图3 渐变焦镜片子午线构造原理图Fig.3 The principal vertical meridian of progressive power spectacles
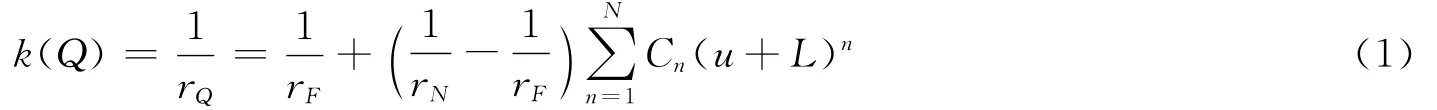
式(1)中,rF、rN和rQ分别表示F,N和Q点曲率半径,Cn为待定系数。
从式(1)可知通过取不同的阶次能够得到不同的子午线光焦度渐增方式,设子午线上任意一点Q的曲率半径为rQ,在Q点处的曲线法线上取一点q(见图3),使Qq=rQ,以q为圆心,rQ为半径作一个圆与子午线相切于Q点,这个圆叫做子午线在点Q处的曲率圆。所以,总可以把子午线上任意一点Q看成在一系列球面的某一个球面上,这些球面的曲率半径从rF逐渐变化成rN。当任意点Q在子午线上移动时,相应的曲率中心q的轨迹曲线mm′称为子午线的渐屈线。所以,任意点Q对应的曲率中心q位于子午线的渐屈线mm′上,长度Qq即为Q处的曲率半径,直线Qq垂直于子午线而与mm′相交于点q。
若用(ε,η,ζ)表示q点的坐标,已知子午线上Q点的x坐标值u和曲率半径r,容易从几何关系得出下面关系式:
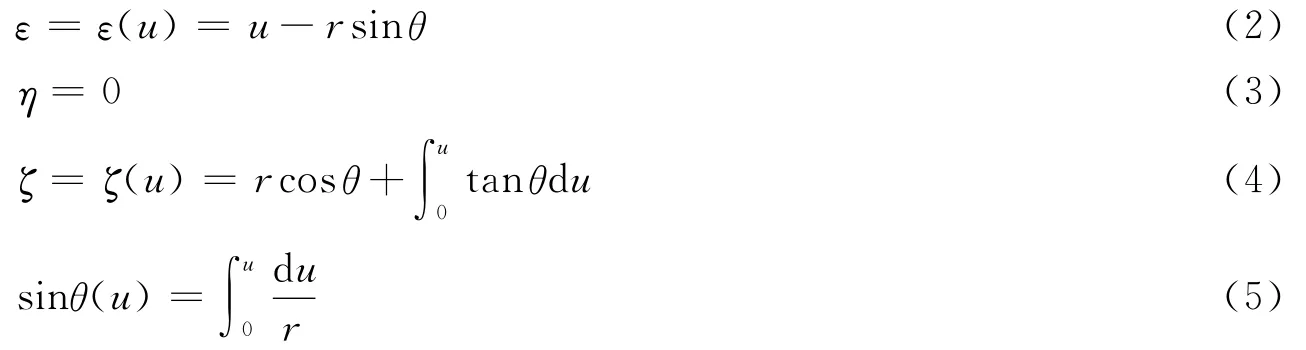
每一个球面与子午线切点的x坐标值u都不相同,所以从圆心坐标和半径可得到这一系列的球面方程为:

由式(1)和式(6)可以确定子午面内光焦度变化方式和密切圆方程,下面进一步确定整个渐变焦的面型。
2.2 渐变焦眼镜片的面型设计
首先在xoy坐标面中定义一个光焦度分布函数ω(x,y),它满足以下边界条件:

渐变焦眼镜的设计思想是在镜片的渐变区做到光焦度平缓渐变,从而解决双光镜存在的视觉阻断、跳跃等现象。若需要函数ω(x,y)平缓渐变,则要求其梯度的平均值达到最小,即下述函数的值最小:
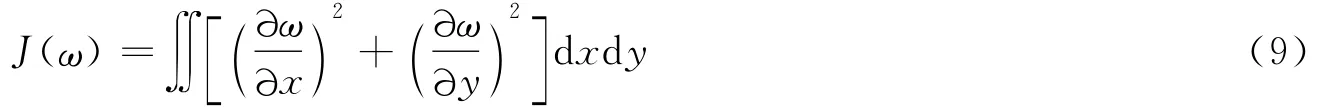
根据变分法中的欧拉-拉格朗日公式可知,当式(9)取最小值时,函数ω(x,y)必须满足拉普拉斯方程[10-11],即

分析到这里可发现等光焦度线需要满足式(7)、式(8)式的边界条件和式(10)的拉普拉斯方程。这样的解很多,需要选择与子午线正交的等光焦度线的曲线形式,等光焦度线可以是直线、抛物线、双曲线、圆或椭圆,其曲线形式的选择需要与镜片佩戴者个性化设计要求相匹配。现采用圆作为等光焦度线,如图4所示。
设通过镜面任一点总存在一个圆柱面和子午线相交,交点x坐标值为u,并且沿着此柱面和坐标面xoy的交线的光焦度值恒等于(u,0)处的光焦度,由式(7)、式(8)和式(10)联立求解可得满足条件的一个近似解[12-14]:
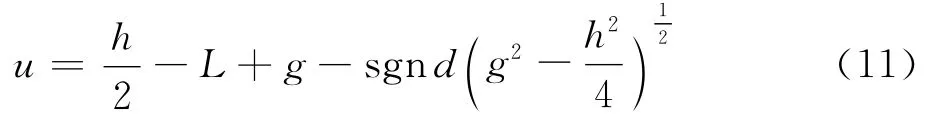
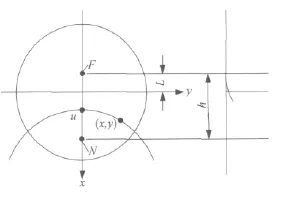
图4 xoy坐标下渐变焦镜片的平面图Fig.4 Veiw in vertical elevation(xoy)of progressive addition lens
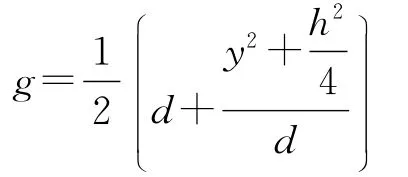
对于-L到-L+h之间的任意一个u值,总存在一个包含等曲率线的圆柱面。这些圆柱面在区间(h-L,-L)中与x轴只有一个交点,这些圆柱面和渐变镜片表面相交处的曲率半径为对应光焦度ω(u,0)的常数。这些交点连起来就成为一条等曲率或者说是等光焦度的交线,这些交线构成了整个渐变镜片的表面。而且,根据前述证明,这些曲线组成的曲面是一个光滑连续渐变的曲面。
将式(11)代入式(2)~式(6)可得渐变焦镜片表面上任意点的矢高表达式:
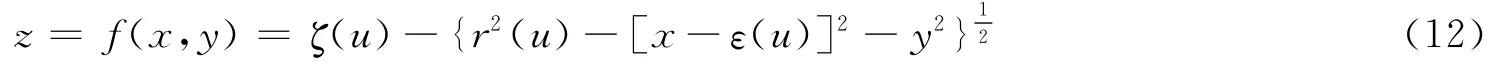
3 子午线上屈光度分布设计的比较
为了比较不同子午线屈光度分布对渐变焦镜片的影响,选择同一镜片参数进行设计:视远点镜片度数为1.0m-1,视远与视近之间的加光度数为1.5m-1,镜片渐变区高度h=18mm,视远点与镜片中心点的间距L=7mm。镜片直径为60mm,折射率n=1.498。
根据式(1)所定义的子午线的N 次多项式,分别取N=8、N=4、N=1设计出3种不同的子午线屈光度分布,如图5所示。三种子午线在视远点和视近点有相同的屈光度值,曲线1为N=4时子午线屈光度分布;曲线2为N=8时子午线屈光度分布;曲线3为N=1时,子午线屈光度分布(呈线性变化)。从图中可以看出,与曲线1相比,曲线2的屈光度在视远点和视近点之间变化较快,而在视远点和视近点附近皆有比较缓慢的稳定变化趋势。曲线3为线性变化,在整个子午线上无屈光度缓慢变化的区域[15]。
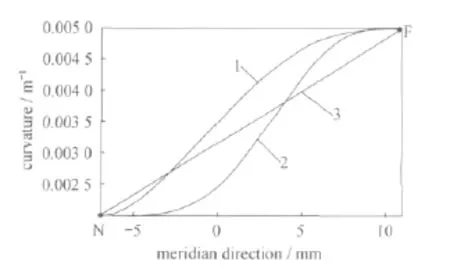
图5 三种子午线屈光度分布图Fig.5 Power curves for three kinds of the meridian line
由此可知,线性变化的曲线3由于接近视远区和视近区时屈光度都变化过快,所以在镜片的过渡区会产生很大的像差。由曲线1设计制作出来的镜片会拥有开阔的、象散较小的视近区域和较为宽阔的渐变区域,但其视远区域狭窄,在实际使用上有一定的局限性。它代表了一个类型的渐变焦眼镜,近距离作业为主的工作人员可以选择佩戴这种眼镜,但如果较长时间使用远视区域就会出现不适反应,所以并不是日常生活的首选。而曲线2虽然使其渐变区域狭窄,在使用渐变区时会产生较大的像差,但其在渐变区过度到远视和近视区时均变化缓慢,可以拥有较为宽阔的视远区和视近区,满足日常生活的使用要求,能够达到设计渐变焦眼镜的要求。
4 设计实例
光焦度增量为2.00m-1的镜片,选取视远区参考点F和视近区参考点N 的光焦度分别为0.5m-1和2.5m-1,选用折射率为1.6的树脂材料作为镜片。取F点和N 点之间距离h=18mm,视远点F与镜片中心点的间距L=7mm,镜片直径为60mm,取N=8并合理选取式(1)中系数Cn,加工得到镜片像散分布图如图6所示。
首先,从设计要求来看镜片实现了从-0.5m-1到-2.5m-1的渐进变化。参照图6可以发现,视远区和视近区像散很小,渐变区通道的像散有所增加,但也相对不大,周边区域像散逐渐增大。故该镜片的测量结果与设计要求相符,佩戴该镜片在视远和视近时都有理想的视觉效果。

图6 渐变焦镜片的像散分布图Fig.6 Contours of constant surface astigmatism of progressive addition lens
5 结 论
根据渐变焦镜片的结构论述了渐变焦镜片的设计思想,介绍了渐变焦镜片运用高阶多项式设计的子午线方程和以圆作为等屈光度轮廓线的面型设计方法,通过采用微分和几何学原理得到渐变焦镜片上任意点的矢高表达式。根据子午线方程给出三种不同的子午线屈光度分布,比较了三种设计所对应的镜片并分析了各自的特点。从上述的结果可见,子午线屈光度变化对渐变焦镜片的设计结果影响较大,根据使用条件,合理选取渐变焦镜片子午线高阶多项式参数,可以设计出满足不同使用要求的渐变焦镜片。
[1]BORISH I M,GRISDALE E.Optical guide[M].陈雄编,译.上海:上海医科大学出版社,1999.
[2]DARRYL M.Fundamentals of progressive adiition lens design[J].SOLA Technical Marketing,1998,26(13):40.
[3]呼正林.实用渐进眼镜学[M].北京:军事医学科学出版社,2004.
[4]瞿 佳.眼镜学[M].北京:北京中国标准出版社,1992.
[5]DAVID P R.Progressive addition lenses:history,design,wearer satisfaction and trends[J].OSA TOPS Vision Science and Its Applications,2000,35:38.
[6]JAMES S E,MARKUS B.Optics of progressive addition lenses[J].Optometrv and Physiological Optics Copyright,2006,35:38.
[7]DIDIA S P,GERARDO T.Ophthalmic lenses measurement using hartmann test[J].SPIE,2004,5622:102-107.
[8]吴泉英.渐进多焦点眼用镜片的子午线设计研究[J].光学学报,2009,29(11):3186-3191.
[9]吴泉英.渐进多焦点镜片的设计方法[J].激光杂志,2009,30(6):12-14.
[10]叶其孝,沈永欢.实用数学手册[M]2版.北京:科学出版社,2006:449-452.
[11]梅向明,黄敬之.微分几何[M]2版.北京:高等教育出版社,1998:89-141.
[12]WINTHROP J T.Progress power ophthalmic lens:US,4514061[P].1989-08-29.
[13]WINTHROP J T.Progress addition spectacle lens:US,5123725[P].1992-07-23.
[14]WINTHROP J T.Hard/soft superposition pressive lens design:US,52726734[P].1998-03-10.
[15]李 笑,孙 惠,李湘宁.渐进多焦点镜片的评价[J].光学仪器,2012,34(2):26-30.

