线性调频步进信号雷达微动目标成像方法

常 沙， 张战兵， 李开明， 李宏静

（①空军工程大学 信息与导航学院，陕西 西安 710077；②西南大学 地理科学学院，重庆 400715）

0 引言

目标或目标部件除质心平动以外的振动、转动等称为微动[1-2]。目标微动会使回波频谱存在旁瓣或展宽，这称为微多普勒效应[1-2]。微多普勒被认为是雷达目标的独特特征，对目标识别与分类具有重要意义[1-3]。

周期性旋转或振动的微多普勒近似为正弦规律的调制[1-3]。在此基础上，V. C. Chen提出利用时频分析方法提取微多普勒[1-2]，Thayaparan T提出采用S时频变换方法计算微多普勒谱图，并采用 Viterbi最短路径算法进行瞬时频率估计[4]；Pawan Setlur通过设计正弦指数基函数来参数化微多普勒信号并实现其分离[5]，又提出迭代加权最小二乘的微动参数估计方法[6]；Li J和Ling H提出自适应chirplet分解方法[7]，实现信号的分解并提取微多普勒信息；文献[8]提出利用扩展Hough变换方法在谱图域搜索正弦曲线参数来提取具有大旋翼目标的微多普勒信息；文献[9]基于经验模态分解法分析了进动锥体目标回波，并利用分离的本征模态函数提取了进动周期等参数；文献[10]提出基于多普勒极值点信息的平动参数提取和平动补偿方法，实现了平动补偿和微多普勒的高精度实时提取。

由于微多普勒极其敏感，对雷达分辨率提要求很高。线性调频步进信号在保持距离高分辨的同时，降低了对雷达系统的硬件要求[11]。在该信号体制下，文献[12]研究了鸟类目标振翅的微多普勒，文献[13]对微动目标运动的距离走动和卷绕进行分析，基于Hough变换方法分离并提取微多普勒信息，但运算量较大。借鉴相消处理的思想，在线性调频步进信号体制下分离并提取目标微动的微多普勒，得到清晰的ISAR像，仿真验证了方法的有效性。

1 线性调频步进信号ISAR成像原理

设线性调频步进信号chirp子脉冲个数为N，子脉冲宽度为T1，子脉冲调频斜率为μ，子脉冲带宽B1=μT1，起始载频为f0，频率步进值为Δf，脉冲重复周期为Tr，则雷达发射的第0簇子脉冲串中的第k个子脉冲可表示为：

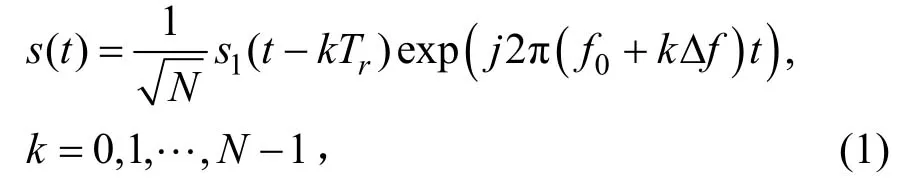
假设目标由J个散射点Pj组成，将发射信号幅度归一化，则第k个子脉冲的回波可写为：

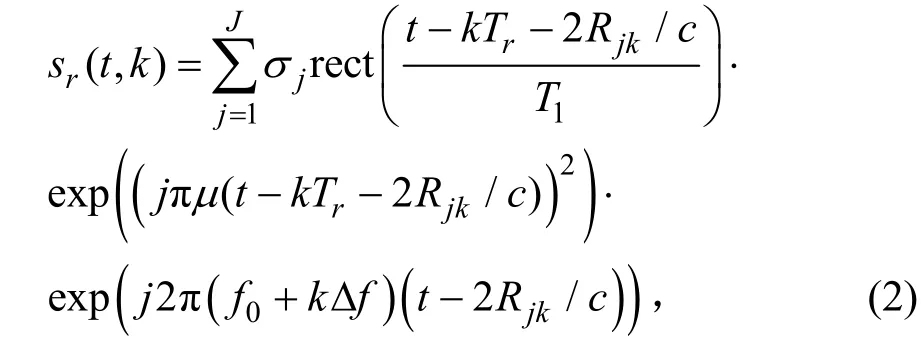
其中Rjk为散射点Pj在发射第k个子脉冲时到雷达的距离。

假设精确的运动补偿已经完成，设参考信号为s0( t, k)，参考点到雷达的初始距离为R0k。则以参考点的时间为基准，将回波信号与参考信号进行拉伸处理后，作关于快时间的FFT并去除RVP（剩余视频相位）和包络斜置项得[12-13]：

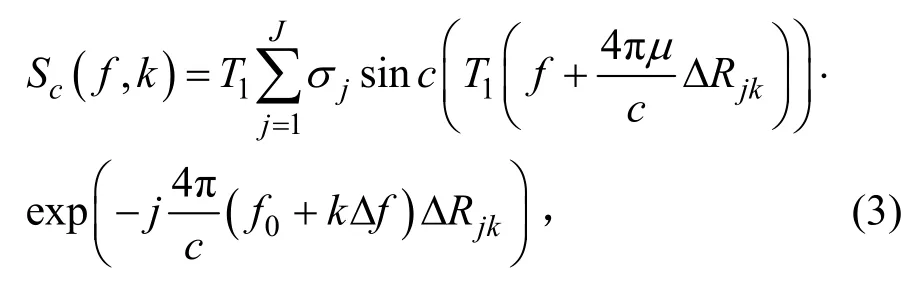
令f=-4πμΔRjk/c ，再对各次粗分辨距离像作关于k的FFT，得：的峰值出现在

文献[13]详细讨论了精分辨距离像不发生卷绕的条件，这里不再赘述。假设成像期间不发生越距离单元徙动，这样，每发射一簇脉冲串都能得到一幅精分辨距离像，发射多簇脉冲串后，对每一个精分辨距离单元作慢时间的 FFT，可得到目标的二维精分辨像。

2 线性调频步进信号微多普勒提取

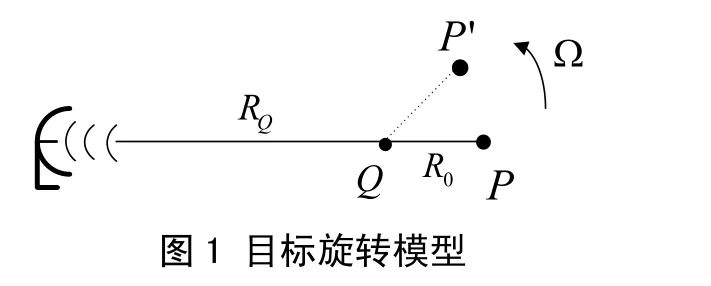
图1为目标旋转模型，点P、Q同时位于雷达视线方向，点Q到雷达的初始距离为RQ，且点P、Q的初始距离为R0。设目标由J个非旋转点Pj和M个旋转点构成，以Q点为参考点，则式(4)可写为：

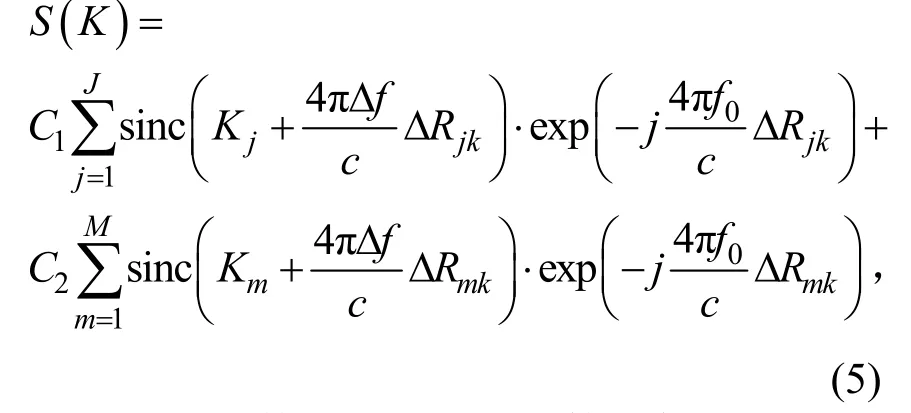
其中C1、C2为常数，ΔRjk为发射第k个子脉冲时非旋转点Pj到旋转中心Q的相对距离，ΔRmk=R0cos Ω t ，为旋转点到旋转中心Q的距离。可见非旋转点和旋转点的精分辨距离像峰值分别位于：

对式(5)两边同时取模（或取模平方），即得到目标的精分辨谱图。

可以看出，在精分辨谱图上，旋转点表现为正弦曲线形式，该曲线周期即为旋转点的运动周期。文献[13]在线性调频步进信号体制下，对旋转目标的微多普勒进行了推导，并对微多普勒正弦曲线的振幅、相位及旋转速度的影响进行了分析。这里重点研究微多普勒的分离与提取。

相消技术(或称“延迟线”技术)是基于固定目标回波振幅不变，将相邻重复周期的信号相减消去固定目标回波，它是雷达信号处理中一种经典的剔除地杂波方法[14]。由于在较短时间内，非旋转点相对于参考点的相对位置近似不变，其对应的直线谱图幅度近似不变，而旋转散射点到参考点的距离周期性地变化。因此，将相消技术应用于精分辨谱图域，相隔一定间隔对精分辨谱图进行相消处理，将直线谱图对消掉，对正弦谱图予以保留，从而分离并提取微多普勒，进而得到目标ISAR像。

在实际信号处理中，S( K )被表示为一个矩阵，不失一般性，设其行向量为慢时间域采样值，列向量为快时间域采样值。因此，对固定慢时间间隔的精分辨谱图进行相消处理可等效为对矩阵的列向量作差。该方法具体步骤如下：

1）保存S( K )的相位到新的矩阵H( K)。

中的直线成分，对正弦谱图进行保留。

5）利用L( K′)与相位矩阵H( K)恢复复矩阵S'(K )，慢时间压缩得到非旋转点的ISAR像。中进一步分离出直线谱图

3 仿真验证

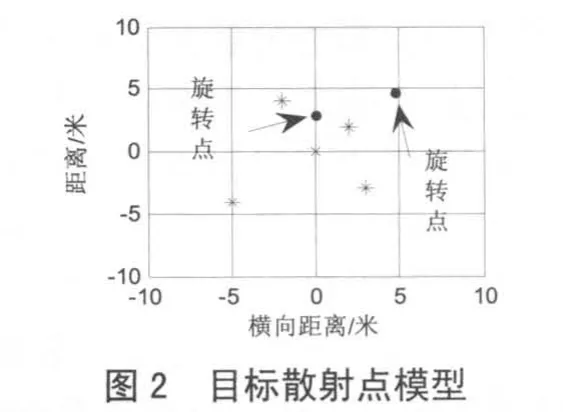
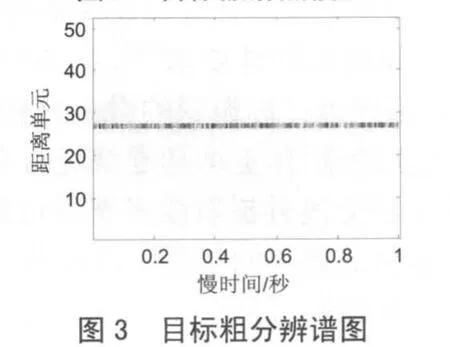
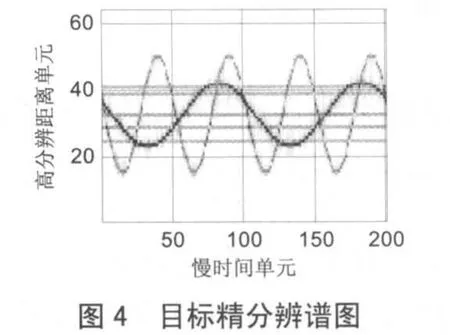
设线性调频步进信号载频为10 GHz，频率步进值Δf＝4.687 5 MHz ，每个脉冲串中包含64个子脉冲，PRF=400，合成带宽B=300 MHz，成像时间为 1 s。目标到雷达的距离为 10 km，运动速度为300 m/s，横向分辨率为0.5 m。图2为散射点模型，两个旋转点围绕(0,0)点旋转，作旋转半径分别为3 m、7 m，旋转频率分别为2 Hz和4 Hz。图3为目标粗分辨谱图，图4为目标精分辨谱图。

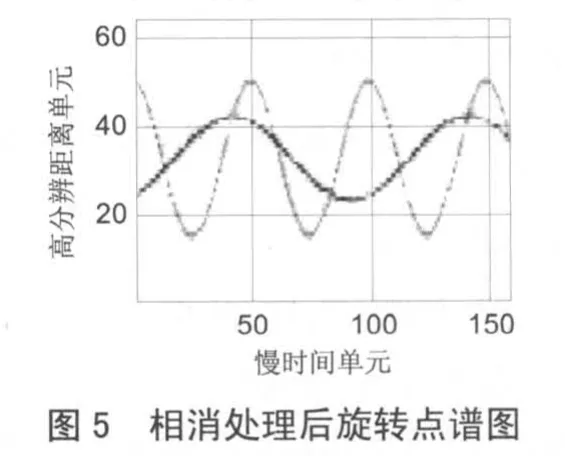
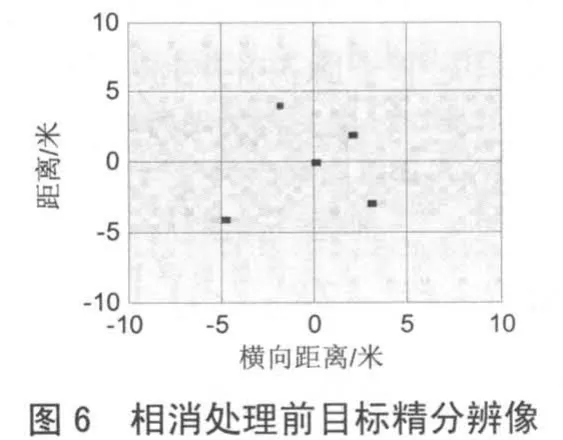
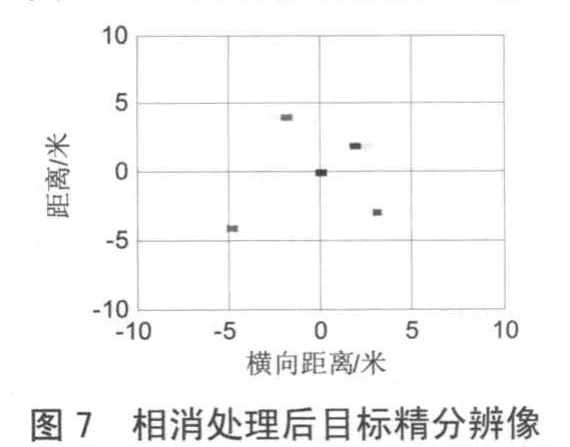
仿真中将目标精分辨谱图相隔 39列进行对消处理，图5为相消处理后得到的正弦谱图，通过相关运算可提取出旋转点的旋转频率和旋转半径等微动信息。图 7为相消处理后目标精分辨像，与图 6相消处理前的精分辨像相比，成像质量有较大提高。仿真表明，该方法对线性调频步进信号下微动目标的微多普勒分离、提取与成像是有效的。

4 结语

在精分辨谱图域，使用相消处理的方法可有效提取目标微动的微多普勒信息，并得到目标清晰的ISAR像。作为高分辨信号，线性调频步进信号可以精细刻画目标微动的微多普勒特征，在 ISAR成像及微多普勒提取方面必将发挥更大的作用。

[1] CHEN V C,LIPPS R.Time-frequency Signatures of Micro-Doppler Phenomenon for Feature Extraction[J]. Proc.SPIE, 2000(4056): 220-226.

[2] CHEN V C, LI F Y, HO S S, et al. Micro-Doppler Effect in Radar: Phenomenon, Model and Simulation Study[J]. IEEE Trans. on AES, 2006, 42(01): 2-21.

[3] 庄钊文,刘永祥,黎湘.目标微动特性研究进展[J]. 电子学报,2007,35(03):520-525.

[4] THAYAPARAN T, STANKOVIC L, DJUROVIC I. Target Detection and Feature Extraction in Indoor and Outdoor Environments Using Micro-Doppler Analysis[R]. Ottawa: Defence Research and Development Canada, 2008.

[5] SETLUR P, AMIN M, AHMAD F. Analysis of Micro-Doppler Signals Using Linear FM Basis Decomposition[C].SPIE Proceedings on Radar Sensor Technology,2006(6210):1-11.

[6] SETLUR P, AMIN M, AHMAD F. Optimal and Suboptimal Micro-Doppler Estimation Schemes Using Carrier Diverse Doppler Radars[C]. Taipei: IEEE International Conference on Acoustics, Speech and Signal Processing, 2009: 3265-3268.

[7] LI J, LING H. Application of Adaptive Chirplet Representation for ISAR Feature Extraction from Targets with Rotating Parts[J].IEE Proc. Radar Sonar Navig.,2003,150(04):284-291.

[8] ZHANG Qun, YEO T S, TAN H S, et al. Imaging of a Moving Target with Rotating Parts Based on the Hough Transform[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(01):291-299.

[9] 牛杰,刘永祥,秦玉亮,等.一种基于经验模态分解的锥体目标微动特征提取方法[J].电子学报,2011,39(07):1712-1715.

[10] 杨有春,童宁宁,冯存前,等.弹道目标中段平动补偿与微多普勒提取[J].宇航学报,2011,34(10):47-49.

[11] 龙腾,毛二可,何佩琨.调频步进雷达分析与处理[J].电子学报,1998,26(12):84-88.

[12] 朱丰,冯有前,罗迎,等.一种基于最小熵准则的鸟类目标ISAR成像新方法[J].通信技术,2008,41(08):198-200.

[13] 罗迎,张群,柏又青,等.线性调频步进信号雷达微多普勒效应分析及目标特征提取[J].电子学报,2009,37(12):2741-2746.

[14] 丁鹭飞,耿富禄.雷达原理[M].第3版.西安:西安电子科技大学出版社,2002.

[15] 石燚,陈光,吴士云.基于窗函数的Chirp-UWBw信号研究[J].通信技术,2010,43(06):43-46.

[16] 夏琳,王艳萍,李黎明.情报作战中的信息伪装技术[J].通信技术,2002(02):47-49.