基于信任度函数的认知无线电频谱感知算法研究

李 转，任旭虎

(中国石油大学(华东)信息与控制工程学院,山东 青岛266555)

认知无线电CR(Coynitive Radio)技术能够感知并分析某个特定区域的频段，找出适合自己通信的“频谱空洞”，利用某些特定的技术来处理利用合适的频段，使其在不影响已有的通信系统的前提下进行工作[1]。如何进行高效的无线频谱分析和估计是认知无线电感知无线环境工作中的关键技术之一[2-3]。频谱分析是一个发展相对成熟的数字信号处理技术，它已经形成了许多具有特色的理论和算法。在认知无线电技术中，也可利用已有的算法进行无线环境检测。

1 信任度函数

在认知无线电系统中，假设有多个认知用户，且第i个和第 j个认知用户测得的数据分别为 xi和 xj，若xi的真实性越高，则认为xi被其他数据所信任的程度就越高[2-3]。 所谓 xi被 xj信任程度，即从 xj来看 xi为真实数据的可能性，这种可能性被称为信任度。为了对测得的数据间的信任度进行统一量化处理，通常定义一个信任度函数f来表示xi被xj信任的程度。根据信任度定义，设：

式(1)中，f为一个连续的下降函数，且 0≤f≤1,则信任度函数可表示为：

式(2)中，mij为融合上限。根据信任度数f的定义，可将其表示为指数函数的形式：

式(3)中|xi-xj|的值越小，bij的值就越大，数据 xi和 xj间的相互信任度就越大。当|xi-xj|的值为0时，bij=1。反之，如果|xi-xj|的值很大，则bij的值很小，说明数据 xi和 xj间的相互信任度bij很小。

由于指数函数 bij在|xi-xj|∈[0,∞]上的取值是 1～0单调递减的，所以满足了信任度函数应该具有的性质。在实际应用中,当|xi-xj|的值超过了设定的上限值mij时，可认为这两个数据已经不再相互信任，此时bij=0。即：

式(4)中，bij为满足模糊性要求的指数函数形式。它既充分利用了模糊理论中信任度函数确定的优点，同时也避免了数据之间相互信任程度的绝对化，更加符合实际问题的真实性，可使融合结果更加精确和稳定。

假设有n个认知用户，根据测得数据间的信任度函数bij，可建立信任度矩阵 B。

对于 B中第i行元素来说，若Σbij(j=1,2,…,n)的值较大，则表明第i个认知用户测得的数据被大多数认知用户信任。反之，信任度较小，即第i个认知用户测得数据为真实数据的可能性较小。

2 数据融合

假设用wi来表示第 i个认知用户测得的数据 xi在融合过程中所占的权重[4]。由于wi值的大小反映了其他认知用户测得的数据对第i个认知用户测得数据xi的综合信任程度，因此可以利用wi对 xi进行加权求和，得到数据融合的表达式：

式(6)中，wi应满足

wi综合了一个关于xi的信任度系统中各子系统bi1,bi2,…,bin的全部信息，因此只需求出一组非负数a1,a2,…,an,使得：

可以将式(7)改写成矩阵形式：

式(9)中,W=[w1,w2,…,wn]T,A=[a1,a2,…,an]T。

由bij≥0可知信任度矩阵B是一个非负矩阵，且该对称矩阵存在最大模的特征值 λ(λ＞0)，使得

可以求出λ及其对应的特征向量A，且A中的分量满足 ai＞0(i=1,2,…n)的条件。 由此可得：

式(11)可作为对各认知用户测得的数据间综合信任程度的度量，即：

对wi进行归一化处理，得到：

因此可求出对所有认知用户测得的数据融合估计的最终结果为：

3 信任度函数在频谱感知中的应用

3.1 频谱感知的基本步骤

基于信任度函数的频谱感知算法是在原来的能量频谱感知算法的基础上提出来的[5-6]，该算法针对未知信号模型，对于各认知用户首先分别采用能量感知算法，然后对感知能量进行归一化处理，再由融合中心确定信任度[7-9]。频谱感知的流程图如图1所示。

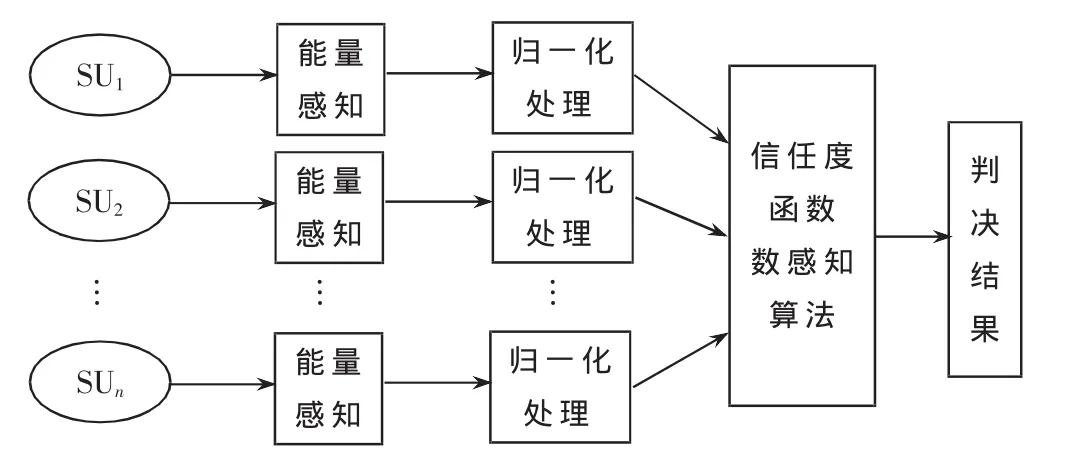
图1 基于信任度函数频谱感知流程图

3.2 仿真及分析

假设具体仿真条件为：5 km×5 km的方形认知无线电网络，单个认知用户SU(Second User)的感知半径RD为500 m。

假设认知用户SU1～SU9在不同时刻利用能量感知算法对主用户是否存在进行多次感知。再将各认知用户的能量统计量归一化处理得到14组数据如表1所示。其中，各认知用户的判决结果取值范围为0～1(若取值接近0则表示主用户信号不存在，接近1则表示主用户信号存在，判决结果在0.5附近时不确定性最大)。

经过多次检验，取 mij=0.2。 当|xi-xj|＞0.2时，bij=0；当|xi-xj|≤0.2时，对一般信任度函数来说 bij=1；对指数信任度函数来说bij=e-|xi-xj|。利用本文提出的方法对14组数据(可看作是14个时刻的检测值)分别进行计算，其中以第2组数据为例，建立信任度矩阵，由矩阵计算得T2时刻一般信任度矩阵和指数信任度矩阵的最大模特征值 λ02、λ′02以及其对应特征向量 B02、B′02(即各信任度所占的权重)分别为：

表1 各认知用户在不同时刻感知信道的利用情况

单从数学的角度来看信任度函数的表达式，一般信任度函数的取值只有0和1两种结果，而指数信任度函数是从0到1变化的[10]。因此，如果用一般信任度函数来处理不确定的信息，可能就会因为主观判断过于绝对化从而会出现错误的判断结果。而对于指数信任度函数来说，当数据较多时可以近似为一个逐渐递减的函数，对不确定信息的判断不会过于绝对化。

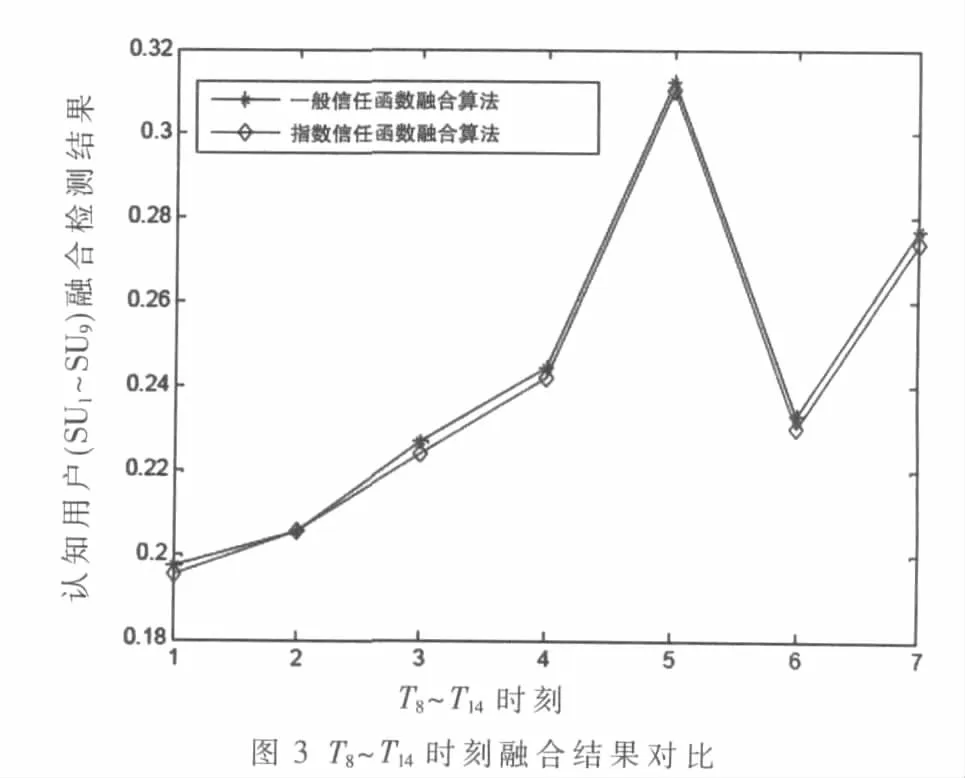
由图2和图3可知，在T1～T7时刻时，指数信任度函数的值大于一般信任度函数的值，在 T8～T14时刻，指数信任度函数的值小于一般信任度函数的值。这就说明若信任度较高，则指数函数的信任度大于一般函数的信任度；若信任度较低，则指数函数得出的信任度小于一般函数的信任度，即指数函数得出的信任度更接近实际的信任度。

对于融合结果来说，若授权用户存在，则融合结果越大越好；反之，融合结果越小越好。例如在T2时刻时，授权用户存在，采用指数信任度函数法和一般信任度函数法得到的融合结果分别为0.801 7和0.798 4。在T8时刻时，授权用户不存在，采用指数信任度函数法和一般信任度函数法得到的融合结果分别为0.195 3和 0.197 4。即采用指数信任度函数法得到的结果更可靠。若某一认知用户的信任度在0.5附近，则它的模糊性很高，但我们希望得到的融合结果能降低这种模糊性。由上述结果可知指数信任度函数法能满足上述要求。

基于信任度函数的认知无线电频谱感算法是考虑不同认知用户和主用户之间的信道环境以及各个用户的感知可靠度的一种算法。采用一般信任度函数时，在可信度范围内认知用户的测量结果就会被完全信任。这样不利于对实际情况做出客观判别，从而导致融合结果受主观因素的影响较大。若使用指数信任度函数，则能满足信任度函数应该具有的特性，使得融合结果更加准确，具有更高的参考价值。由实际应用结果可知，采用指数信任度函数法得到的最终数据融合结果比一般信任度函数法得到的结果更加精确，并使数据融合过程具有更好的抗干扰性。

[1]吴今培,孙德山.现代数据分析[M].北京：机械工业出版社,2006.

[2]周贤伟,王建萍,王春江.认知无线电[M].北京：国防工业出版社,2008.

[3]冯文江,郭瑜,胡志远.认知无线电中的频谱感知技术[J].重庆大学学报(自然科学版),2007，30(11)：46-49.

[4]焦竹青，熊伟丽，张林，等.基于信任度的多传感器数据融合及其应用[J].东南大学学报，2008,38增刊(1)：253-257.

[5]林威,吴捷,张钦宇,等.基于认知无线电系统合作检测的数据融合研究[J].通信学报，2009(10)：135-140.

[6]卞荔，朱琦．基于数据融合的协作频谱感知算法[J]．南京邮电大学学报(自然科学版),2009，29(2)：73-78.

[7]杨志伟,杨家玮.认知无线电中的一种干扰温度估计算法[J].通信技术,2006,39(12)：128-130.

[8]SAHAI A,HOVEN N,TANDRA R.Some fundamental limits in cognitive radio[C].Allerton Conf.on commun[C].Control and Computing 2004,October,2004.

[9]殷振华,耿志,刘郁林,等.基于能量检测的频谱感知方法的介绍[J].通信技术,2007,40(11)：83-85.

[10]胡振涛,刘先省.基于相对距离的一种多传感器数据融合方法[J].系统工程与电子技术,2006,28(2)：196-198.