纯滚动隔震系统位移计算方法的对比分析
魏 标,戴公连,于向东,曾庆元,王军文
(1.中南大学 土木工程学院,长沙410075;2.石家庄铁道大学 土木工程学院,石家庄050043)
关于隔震,新西兰、美国、日本、意大利等国主要通过引入隔震装置来延长结构的基本周期,避开地震能量集中的范围,从而减小主体结构地震反应,代表性的隔震装置有分层橡胶支座、铅芯橡胶支座、高阻尼橡胶支座等[1],相应隔震结构有一固定水平刚度或者水平刚度范围,对应着一固定周期或者周期范围。因此,如果实际发生的地震频谱特性与设计地震不同,结构可能发生共振现象;如果实际发生的地震加速度比设计地震大,隔震层在发生较大位移的同时,传给结构的地震力仍很大,结构可能遭受破坏[2]。
为了真正隔离地震,已有研究者开始关注以滚动为基础的隔震方法。为了避免软场地震波对墨西哥城建筑的破坏,墨西哥Flores等设计了一种滚球装置,用来取代传统的橡胶支座,并已安装在墨西哥城的一幢5层钢筋混凝土框架结构的教学楼的柱脚处[3]。美国Lee等发明了一种由2层滚轴组成的滚动隔震支座,并尝试应用于高速公路桥梁[4-5]。印度Jangid等起初认为椭圆形滚轴比圆形滚轴隔震效果更好,之后又认为圆形滚轴装配恢复力装置后,具有较好的隔震效果[6-7]。葡萄牙 Guerreiro等[8]提出了一种滚球隔震装置,并尝试用来保护轻型结构或装置。中国曾庆元指导博士生舒文超[9],通过理论分析和振动台试验指出,对于纯滚动隔震系统,地震作用下,地面运动传递给结构的地震力可以预先控制为一很小值,从而避免结构破坏[9-11];另外,隔震层以上的主体结构基本呈平动状态,如能准确预测隔震层的位移反应,即基本预测了整个结构的位移反应。
目前,对于结构中的摩擦现象,一般采用刚塑性力 位移曲线来简单描述摩擦性能,并计算相应结构的地震反应(简称为“传统的刚塑性力 位移曲线方法”)。为了更加合理地分析纯滚动隔震系统的地震位移反应,笔者根据滚动摩擦的性能特点,首先编制了数值分析程序,然后与传统的刚塑性力 位移曲线方法进行了实验对比,最后对比分析了这2种理论方法在简谐振动和地震作用下计算结果的差异。
1 数值分析程序
在分析纯滚动隔震系统运动特点的基础上,建立了数学模型,并编制了数值分析程序。
1.1 数值分析程序原理
地震作用下,纯滚动隔震系统的位移反应是一个复杂过程——地面和结构都在运动。为了描述地面和结构的运动,定义空间中的绝对位移坐标如图1所示。另外,已有研究表明[9],对于纯滚动隔震系统,地震作用下的主体结构基本呈平动状态,这里假定隔震层以上的主体结构为刚体。

图1 纯滚动隔震系统
根据地面运动速度ve与结构运动速度vs的大小对比,可以将纯滚动隔震系统的位移反应分为以下几种情况:
1)ve>vs,说明结构与地面之间有相对运动,作用于结构的摩擦力μmg使结构产生加速度μg。
2)ve<vs,说明结构与地面之间有相对运动,作用于结构的摩擦力-μmg使结构产生加速度-μg。
3)ve=vs,说明结构与地面之间没有相对运动,这有2种可能:结构与地面都是静止的,这一般对应着地震开始发生的时刻;结构与地面都是运动的,但在某些时刻,两者速度相同。但上述2种可能仍只是表面现象,为了预测结构下一刻的运动,需要比较此时地面的加速度绝对值与μg的大小:
另外,对于ve>vs或ve<vs的情况,当时,可以判定结构下一刻将随地面一起运动(包含静止状态),即ve=vs,其中,Δti为地震动输入数据的时间间隔。联合3)情况(2),便建立起了结构运动速度vs与地面运动速度ve的3种关系之间的转化。
1.2 数值分析程序的编写
根据以上分析,结构地震位移反应的计算流程图如图2所示,并采用Tcl/Tk语言编写了数值分析程序(为独立程序,不是大型软件的二次开发子程序)。
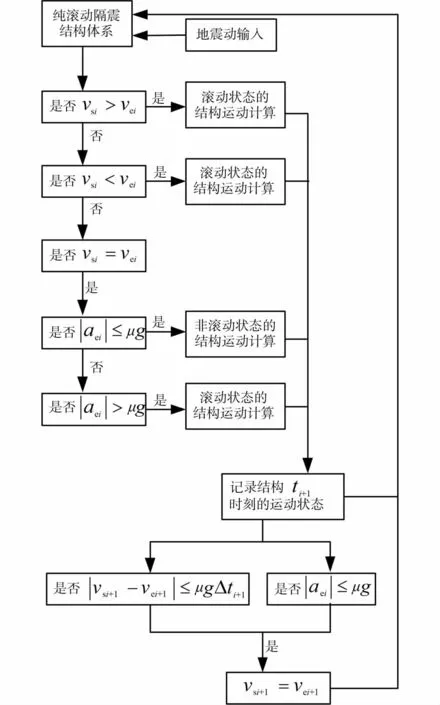
图2 数值分析程序的计算流程图
备受关注的结构地震反应主要为结构地震力和相对位移。已有研究表明[9],对于纯滚动隔震系统,地震作用下,地面运动传递给上部结构的地震力近似为隔震层的摩擦力,可以预先确定,所需计算的结构地震反应仅为结构的相对位移。所以,本程序主要针对结构位移反应的计算而编写。
2 实验验证
分别进行模型实验、数值分析程序计算和传统的刚塑性力 位移曲线方法计算,最后进行对比,主要完成2个目标:首先验证数值分析程序是否正确;然后考察传统的刚塑性力 位移曲线方法是否合理。
2.1 实验方案
1)首先在室内墙壁上做好刻度标记,作为绝对位移坐标;然后在地面上放置一块可移动薄板,手工拉动薄板做随机非匀速水平往复运动,用于模拟地面运动;薄板上放置滚球,作为隔震装置;滚球上放置混凝土块,用于模拟结构。实验示意图如图3所示。
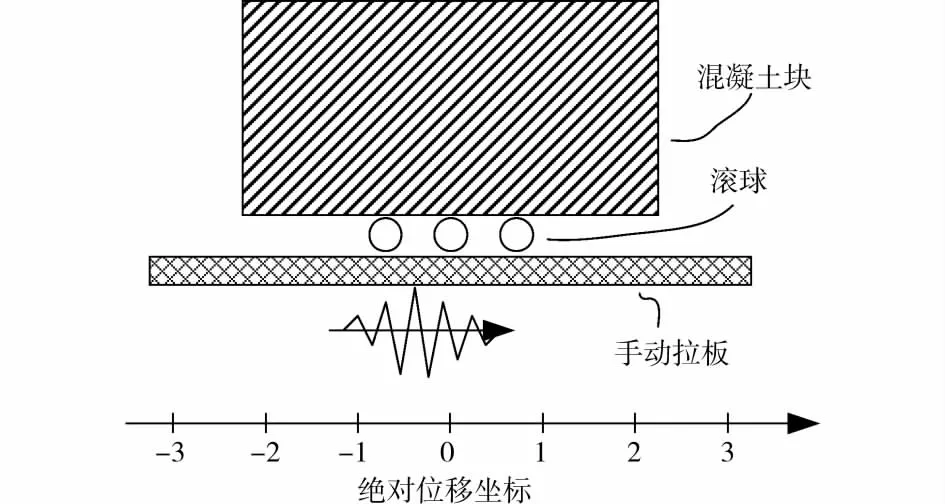
图3 实验示意图
2)在手工拉动薄板运动的过程中,采用数码相机拍摄录像,记录手动拉板和混凝土块的每一时刻的绝对位移,即位移时程曲线。
3)对手动拉板的位移时程曲线进行求导处理,得到手动拉板的速度时程曲线和加速度时程曲线。
4)将得到的手动拉板的加速度时程曲线作为地震动输入,并分别采用数值分析程序和传统的刚塑性力 位移曲线方法计算,得到混凝土块的理论位移时程曲线。
5)对比混凝土块的实验位移时程曲线与2种理论方法得到的位移时程曲线。
2.2 实验材料和实验步骤
所采用的实验材料如下:
1)混凝土块的尺寸为0.8m×0.2m×0.1m,重0.4kN。
2)手动拉板采用木板。
3)滚球采用钢球,直径为0.01m,40个。
经手动拉板、滚球和混凝土块的组合,测得滚动摩擦系数为0.008。
按照图3,进行20次实验。对于每次实验,手工拉动移动板的时间为20~60s不等,实验数据记录间隔为0.1s。
2.3 实验结果
将理论方法(包括数值分析程序和传统的刚塑性力 位移曲线方法)计算的结构相对位移时程曲线的最大值简称为“理论计算最大位移”,将实验得到的结构相对位移时程曲线的最大值简称为“实验最大位移”,最后,将“理论计算最大位移”与“实验最大位移”的比值绘于图4中。
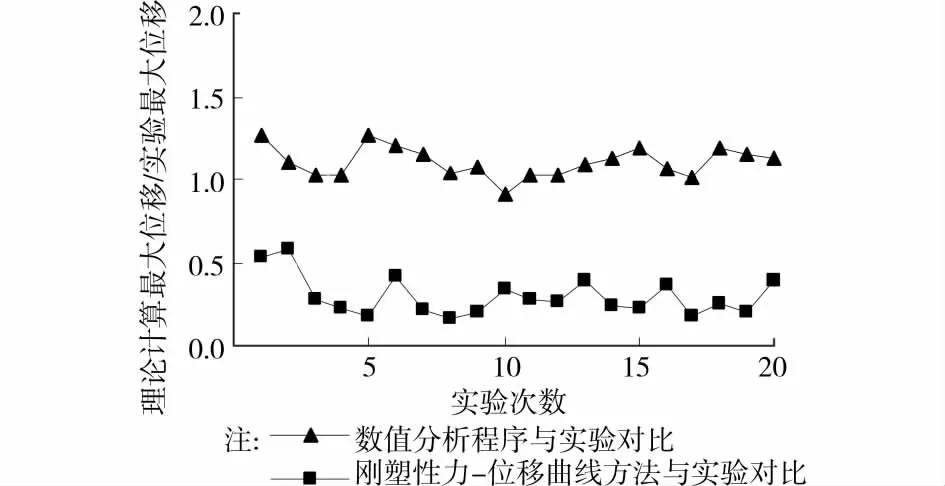
图4 实验结果与理论分析结果的对比
从图4看出,数值分析程序得到的“理论计算最大位移”与实验得到的“实验最大位移”的比值位于0.9~1.3区间内,说明数值分析程序结果总体上比较精确,且比较保守;传统的刚塑性力 位移曲线方法得到的“理论计算最大位移”与实验得到的“实验最大位移”的比值位于0.2~0.6区间内,说明传统的刚塑性力 位移曲线方法的计算结果总体上偏小,且偏于不安全,不合理。
对于传统刚塑性力 位移曲线方法计算结果的不合理性,有没有理论上的深层原因,是值得深入分析的。
对于纯滚动隔震系统,结构的力 位移关系一般表达为图5,它使得传递到结构的地震力预先控制为一固定值或固定范围,近似为隔震层摩擦力。
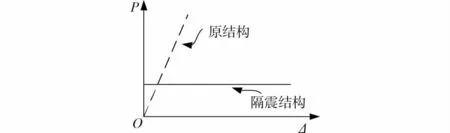
图5 纯滚动隔震系统的力 位移关系的一般表达方式
然而,图5中的力仅仅是对应每一相对位移值Δ时,隔震层传递到结构的地震力的最大包络值,而非真实值。例如,如果在某一时刻,结构与地面同速运动,即使结构已经发生了某一相对位移Δ,此时滚动隔震层传递到结构的地震力应为0,而非图5中的力。所以,采用传统的刚塑性力 位移曲线(图5中的水平线)来简化计算纯滚动隔震系统的地震位移反应,则过于粗糙,理论上存在不合理性。
相反,由于数值分析程序能合理反映纯滚动隔震系统在每一瞬间的力 位移关系,所以计算结果与实验结果比较接近。
3 2种理论方法在谐振作用下的对比
任何周期荷载均可用一系列谐振荷载项来表示,下面研究正弦波输入下的结构位移反应。首先选定正弦波和结构的隔震层摩擦系数,然后分别采用传统的刚塑性力 位移曲线方法和数值分析程序计算,最后对计算结果进行对比分析。
3.1 正弦波和隔震层摩擦系数
所采用的正弦波如下,持续时间为80s。

其中:ω为频率,分别采用31.4、20.93、13.96、8.97、1.57、0.79s-1,对应周期T分别为0.2、0.3、0.45、0.7、4.0、8.0s;a为加速度峰值,分别采用0.4~20.0(间隔0.02s,单位 m/s2)。
隔震层摩擦系数取为0.02。
3.2 分析结果
对于每一周期T对应的正弦波输入,分别将传统的刚塑性力 位移曲线方法计算的结构最大相对位移和数值分析程序计算的结构最大相对位移的比值绘于图6。
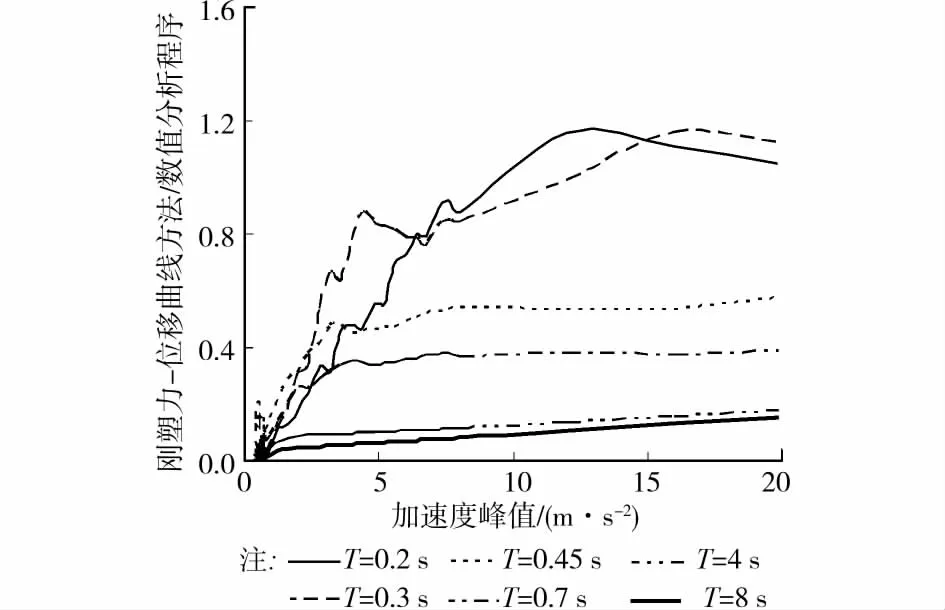
图6 传统的刚塑性力-位移曲线方法与数值分析程序计算的结构最大相对位移的比值
根据图6,可以看到以下规律:
1)总体上,传统的刚塑性力 位移曲线方法得到的结构最大相对位移远小于数值分析程序得到的结构最大相对位移,前者偏于不安全。
2)只有在正弦波周期T较短且加速度峰值a较大的情况下,两者才比较接近。
之所以能出现规律2),主要因为正弦波是一种比较特殊的输入,地面运动始终是同方向的,而且,正弦波周期T越短且加速度峰值a越大,超越滚动临界状态的时间比例就越大。此时,对于纯滚动隔震系统,在多数时间内,传统的刚塑性力 位移曲线与数值分析程序每一瞬间的力 位移关系曲线总体上比较一致,计算结果将比较接近。
4 2种理论方法在地震作用下的对比
地震波不同于正弦波,前者地面运动不是始终同方向的,下面研究地震波输入下的结构位移反应。首先选定地震波和结构的隔震层摩擦系数,然后分别采用传统的刚塑性力 位移曲线方法和数值分析程序计算,最后对计算结果进行对比分析。
4.1 地震动输入和隔震层摩擦系数
对于中国公路工程抗震设计规范(JTJ 004-89)中的II类场地反应谱,采用Simqke程序[12]生成加速度时程波作为地震动输入,加速度峰值分别采用0.2~0.8g(间隔0.01g),持续时间为40s。
隔震层摩擦系数取为0.002~0.03(间隔0.002)。
4.2 分析结果
采用数值分析程序得到的结构最大相对位移与地面最大绝对位移的比值见图7;采用传统的刚塑性力 位移曲线方法得到的结构最大相对位移与地面最大绝对位移的比值见图8。
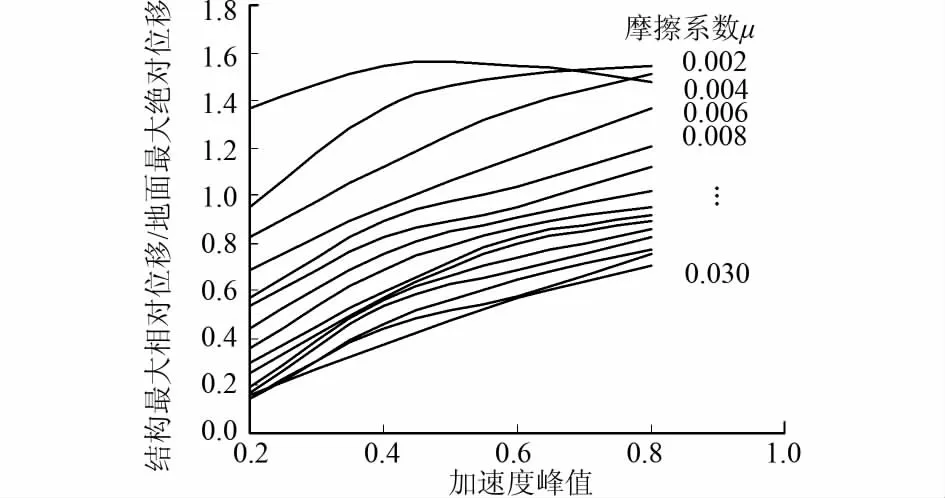
图7 数值分析程序结果
对于相同的地震动输入,地面最大绝对位移是一固定值,与分析方法无关,所以,通过对比图7和图8,可以看出数值分析程序和传统的刚塑性力 位移曲线方法得到的结构最大相对位移的大小对比。
对比图7和图8,可以得到以下规律:
1)针对结构最大相对位移与地面最大绝对位移的比值,隔震层摩擦系数对于数值分析程序的影响程度很大,对于传统的刚塑性力 位移曲线方法的影响程度相对较小。
2)数值分析程序得到的结构最大相对位移远大于传统的刚塑性力 位移曲线方法得到的结构最大相对位移。在隔震层摩擦系数较小的情况下,这种规律更加突出。
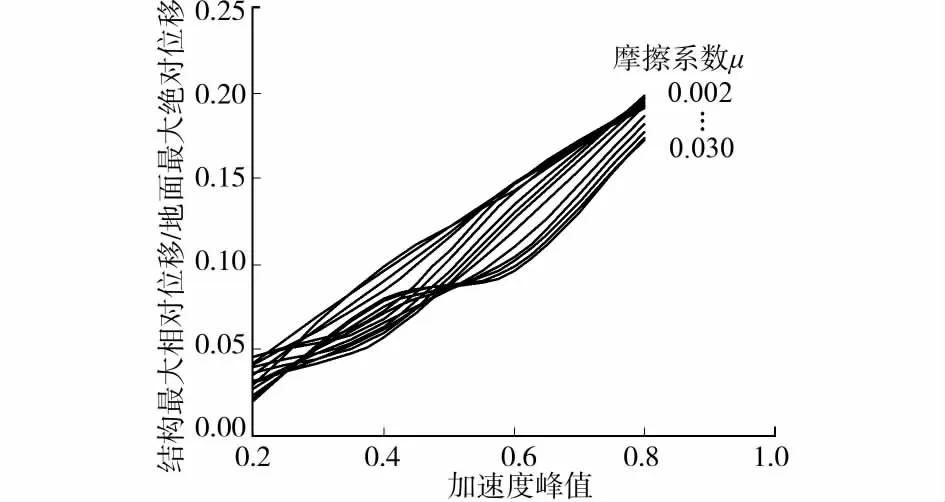
图8 传统的刚塑性力-位移曲线方法结果
另外,从图7看出,结构最大相对位移与地面最大绝对位移的比值是可能超过1.0的。而对于图8,无论如何增大加速度峰值(图中未显示),结构最大相对位移与地面最大绝对位移的比值都无法超过1.0。结构最大相对位移与地面最大绝对位移的比值,在理论上是否会超过1.0?是值得深入分析的。
理论上,对于纯滚动隔震系统,地面可以很大的加速度运动,而结构的最大加速度绝对值仅为μg,所以结构的运动趋势往往滞后于地面。例如,如果最初地面缓慢往正方向运动,那么,结构将随之往正方向运动;不久,如果地面突然朝反方向运动,并在短时间发生很大的位移,而此时结构由于具有一个朝正方向运动的速度,且最大加速度-μg不足以迅速改变结构的惯性运动,那么,在较短的时间内,结构的绝对位移和地面的绝对位移是反方向的,即结构的相对位移(结构的绝对位移和地面的绝对位移的差值)的绝对值大于地面的绝对位移的绝对值,也就是两者的比值出现了大于1.0的情况。
下面进行实例分析,取加速度峰值0.2g,隔震层摩擦系数0.002。采用数值分析程序和传统的刚塑性力 位移曲线方法得到的结果分别见图9和图10。
根据图9,对于地震波,在0~25s区间,正方向的位移变化较为平缓,而负方向的位移变化较为湍急。根据上述理论分析,结构最大相对位移与地面最大绝对位移的比值超过1.0,是正确的。同时,还可以看出,就位移曲线形状来讲,结构绝对位移滞后于地面绝对位移。这说明,数值分析程序是合理的。
图10则无法反应上述规律。图10中,结构基本与地面同步运动,无滞后现象,与理论上的逻辑相矛盾。传统的刚塑性力 位移曲线方法夸大了滞回阻尼的作用[13],导致计算得到的结构最大相对位移偏小,是不合理的。
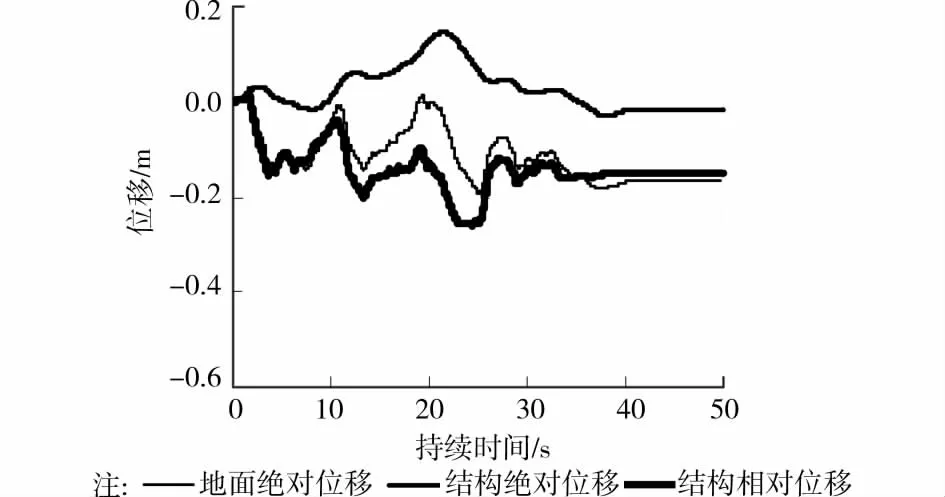
图9 数值分析程序结果
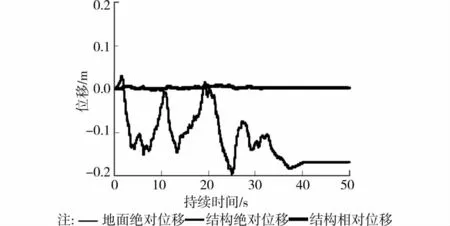
图10 传统的刚塑性力-位移曲线方法结果
5 结 论
针对纯滚动隔震系统的地震位移特点,编制了数值分析程序,并与传统的刚塑性力 位移曲线方法进行了实验对比和理论对比。主要得到以下结论:
1)纯滚动隔震系统的运动可以分解为多种基本运动过程,可以通过数值分析方法求解。所编写的数值分析程序总体上比较合理,计算结果比较精确,并偏于保守。
2)传统的刚塑性力 位移曲线方法不适合计算纯滚动隔震系统的地震位移反应,否则计算结果偏小,且偏于不安全。
需要说明的是,对于隔离地震力来讲,纯滚动隔震系统是一个非常理想的隔震系统,但可能导致过大的地震相对位移。在今后的研究中,可以在纯滚动隔震系统的基础上,加设阻尼装置和恢复力装置,用于减小结构相对位移和震后残余位移,此时,是否有负面影响,以及如何进行数值分析,都是需要进一步研究的内容。
[1]Priestley M J N,Seible F,Calvi E M.Seismic design and retrofit of bridges[M].New York:John Wiley &Sons,1996.
[2]Fan F G,Ahmadi G,Mostaghel N,et al.Performance analysis of aseismic base isolation systems for a multistory building [J].Soil Dynamics and Earthquake Engineering,1991,10(3):152-171.
[3]李宏男,霍林生.结构多维减震控制[M].北京:科学出版社,2008.
[4]Ou Y C,Song J W,Lee G C.A parametric study of seismic behavior of roller seismic isolation bearings for highway bridges [J].Earthquake Engineering and Structure Dynamics,2010,39:541-559.
[5]Lee G C,Ou Y C,Niu T C,et al.Characterization of a roller seismic isolation bearing with supplemental energy dissipation for highway bridges [J].Journal of Structural Engineering,2010,136(5):502-510.
[6]Jangid R S,Londhe Y B.Effectiveness of elliptical rolling rods for base isolation[J].Journal of Structural Engineering,1998,124(4):469-472.
[7]Jangid R S.Stochastic seismic response of structures isolated by rolling rods [J].Engineering Structures,2000,22:937-946.
[8]Guerreiro L,Azevedo J,Muhr A H.Seismic tests and numerical modeling of a rolling-ball isolation system[J].Journal of Earthquake Engineering,2007,11:49-66.
[9]舒文超.桥梁与房屋结构水平地震力隔离理论与试验研究[D].长沙:长沙铁道学院,1998.
[10]史红福,樊剑,李黎.滚动基础隔震机构的动力分析[J].振动与冲击,2005,24(6):91-94.SHI Hongfu,FAN Jian,LI Li.Dynamic analysis of structure isolated by rolling base [J].Journal of Vibration and Shock,2005,24(6):91-94.
[11]王荣辉,许群,舒文超,等.竖向弹簧—钢球隔震系统的隔离水平地震作用[J].华南理工大学学报:自然科学版,2003,31(6):20-25.WANG Ronghui,XU Qun,SHU Wenchao,et al.Horizontal earthquake isolating funetion of the vertical spring-steel rolling base isolation seismic system [J].Nature Science of Journal of South China University of Technology,2003,31(6):20-25.
[12]Fahjan Y,Ozdemir Z.Scaling of earthquake accelerograms for non-linear dynamic analysis to match the earthquake design spectra [C]//The 14th World Conference on Earthquake Engineering,Beijing,China,2008.
[13]Clough R W,Penzien J.Dynamics of structures[M].New York:Mc Graw-hill,Inc,1993.

