持续小强度降雨入渗对非饱和土边坡稳定性的动态影响
刘子振,言志信,彭宁波,段 建,任志华
(1.兰州大学a.西部灾害与环境力学教育部重点实验室;b.土木工程与力学学院,兰州730000;2.台州学院 建筑工程学院,浙江 台州318000)
持续降雨入渗导致滑坡是重大地质灾害之一,降雨诱发滑坡灾害的形成机理和准确预测仍然是一大难题。在雨水的不断侵蚀下,土边坡的地质特性和物理力学特性也在不断变化。持续降雨渗入边坡后,一方面,雨水入渗对土体有切割作用;另一方面,坡体含水量增加,负孔隙水压力减小,使土体的抗剪强度处于动态降低过程,最终导致边坡失稳。国内外学者针对降雨诱发的饱和-非饱和土边坡失稳作了大量的研究。Fredl und等[1-3]提出了双变量非饱和土抗剪强度公式,建立了土体含水量与抗剪强度的关系,拟合了土-水特征曲线方程,随着雨水渗入边坡后,土体内的基质吸力不断降低,导致土体抗剪强度降低。Au[4]全面分析了暴雨引发香港边坡失稳灾害情况。Collins等[5]研究了降雨引发滑坡的原理,认为降雨形成的孔隙水压力影响了边坡稳定,并通过极限平衡理论和有限元方法分析降雨条件下的边坡稳定性。Mohamed等[6]通过改装试验研究了不饱和土抗剪强度与水土特征曲线的关系。Chu-Agor等[7]、Huang等[8]、Oh等[9]等分析了降雨入渗对土体抗剪强度及边坡稳定性的影响。吴宏伟等[10]研究了雨水入渗对非饱和土坡的参数影响。李萍等[11]运用饱和-非饱和渗流有限元法模拟土质高边坡的降雨渗流场。李兆平等[12]以土壤体积含水率作为控制变量,应用非饱和土水分运动基本理论建立了降雨入渗过程中土体瞬态含水率的计算模型,并通过实际工程,讨论了降雨入渗对土质边坡稳定性的影响。
以上研究主要基于非饱和土理论和渗流理论,考虑降雨入渗过程中孔隙水压力增加或基质吸力减小导致的土体抗剪强度降低,没有分析小强度降雨入渗的影响,而且没有分析持续入渗时间对边坡稳定性的影响。而当降雨强度很小或降雨入渗强度较小时,非饱和土边坡内渗流场的影响较小,土体主要是吸湿过程。土体吸湿后,容重增大,力学强度显著降低,导致边坡失稳破坏。随着降雨持续进行,降雨历时、入渗强度、土体抗剪强度和边坡安全系数之间存在一定的定量关系。笔者研究了降雨入渗强度较小时,非饱和土边坡抗剪强度与含水量和降雨持续时间关系,揭示边坡失稳动态过程。运用强度折减法[13-15]求解边坡持续小强度降雨过程的渐进破坏模式及动态安全系数。
1 小强度降雨条件下非饱和土边坡数值计算
1.1 建立非饱和土抗剪强度与含水量关系
边坡土体抗剪强度是影响边坡稳定性的最主要因素,影响土体抗剪强度的主要参数有凝聚力、内摩擦角和基质吸力。基质吸力对非饱和土的力学特性有重要作用,基质吸力会因土体含水量的变化而改变,当土体达到饱和时,基质吸力为零。Fredl und等[1-3]对非饱和土特性作了深入研究,提出了非饱和土抗剪强度理论,见式(1),

式中:τf为非饱和土抗剪强度;为土体的有效凝聚力;为土体的内摩擦角;σ为土体的总应力;ua为土体内的孔隙气压力;us为土体的基质吸力,us=(ua-uw),uw为孔隙水压力;φb为随基质吸力变化的内摩擦角,当土体接近饱和时,φb接近。
令:

式中:c为土体的总凝聚力。
将式(2)代入式(1),得式(3),

当土体达到饱和时,可得式(4)。

非饱和土的含水量对抗剪强度的影响主要通过有效凝聚力c′,内摩擦角φ′和基质吸力us来体现。通过试验可以确定非饱和土含水量与抗剪强度参数的关系,并将非饱和土抗剪强度及相关参数与含水量的变化关系拟合成曲线[16-17]。
有效凝聚力与含水量之间可按式(5)拟合。

将内摩擦角与含水量之间按近似直线拟合,见式(6)。

基质吸力与含水量之间可按式(7)拟合,

式(5)~(7)中:A、B、D、E、F、G和H 为待定系数。
假定降雨入渗经过时间t后边坡内含水量与入渗强度关系为

式中:e为降雨入渗强度,mm/s;λ为待定参量,mm-1;t为降雨持续时间,s;ω0为土体初始含水量。
因此,通过持续降雨入渗强度和时间可得到土体的含水量,进而获得降雨入渗边坡的动态稳定性情况。
1.2 建立抗剪强度与降雨历时的计算式
降雨入渗条件下,边坡土体吸湿后,土体含水量的增加影响边坡的稳定性。以土体含水量作为抗剪强度的主要控制参量,运用FLAC3D有限差分的强度折减法,求解边坡渐进破坏下的安全系数Fs,分析不同含水量时边坡的动态稳定性。按强度折减法原理,定义安全系数为边坡土体的实际抗剪强度与临界破坏时的折减后强度的比值,即:
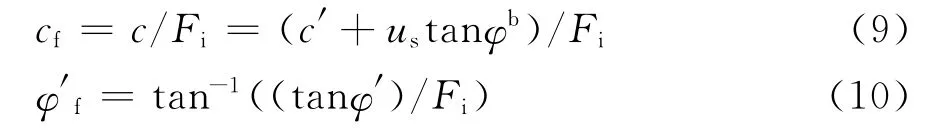
式中:cf和为土体折减后的抗剪强度指标;Fi为不断变化的折减系数,边坡达到临界破坏时的Fi即为边坡安全系数Fs。
土体处于非饱和状态时,小降雨入渗在坡体内处于吸湿过程,坡体内渗流影响较小。用Fredl und等提出的非饱和土抗剪强度理论[3],可以得到基质吸力对边坡稳定性的影响。将式(5)~(7)分别代入式(9)、(10)后,可以建立边坡土体含水量与折减强度的关系式,见式(11)、(12)。
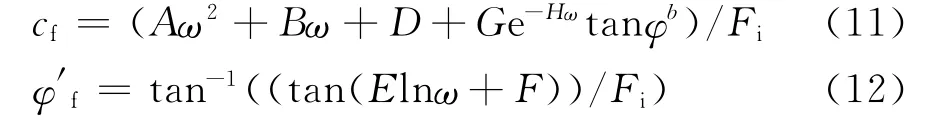
将式(8)分别代入式(11)、(12),得式(13)、(14)。

在持续降雨作用下,土的吸湿饱和过程比较缓慢,边坡体附加的雨水作用力可看作入渗雨水形成的均布荷载q,见式(15),

式中:ρ为水的密度,h为降雨入渗的积水厚度。
因此,通过数值计算,可以得到降雨入渗条件下非饱和土边坡的渐进破坏模式和动态安全系数,从而可以得到出边坡失稳时降雨强度和降雨持续时间的临界值。
1.3 计算持续小强度降雨条件下边坡安全系数
降雨入渗后,受影响区域土体吸湿引起抗剪强度不断减小,导致边坡处于动态的不稳定过程。根据边坡稳定性力学机理,以土体弹塑性理论为基础,通过含水量对土体抗剪强度特性的影响规律,确定抗剪强度指标cf(ω)、φ′f(ω)和us(ω)随含水量(或时间)的定量变化关系。随着降雨入渗持续进行,降雨影响区域不断扩大[18],通过强度折减法求得不同含水量时边坡的安全系数 Fs(ω)。当 Fs(ω)<Fs(工程规定值)时,判定边坡破坏(见图1)。

图1 安全系数计算程序
运用强度折减法分析边坡稳定时,必须有能够反映边坡失稳破坏的依据判断依据[13-15]:非饱和土边坡失稳破坏主要由于降雨入渗引起土体的凝聚力cf(ω)和内摩擦角(ω)不断减小,以及土体容重增加,导致边坡破坏,通过FLAC3D分析可以得到贯穿整个边坡的强度最弱滑动带。
通过计算,求得边坡失稳时间及相应的含水量,判别边坡失稳时的非饱和状态。因此,可以通过监测边坡土体的含水量和降雨持续时间来判定边坡的稳定状态,为边坡防护提供依据。
2 工程应用分析
2.1 工程概况
某土边坡位于亚热带多雨地区,在持续的小强度降雨入渗后,边坡失稳破坏(图2)。降雨入渗后,土体吸湿后的抗剪强度显著降低,随着降雨持续进行,土体含水量增加。边坡物理力学参数见表1,降雨影响边坡的计算模型如图3所示,纵向宽度取1 m。土体初始处于非饱和状态,含水量ω0=21%,吸力摩擦角取为土体饱和时的内摩擦角,基质吸力采用张力计测得。降雨入渗强度e=1.93×10-4mm/s,雨水渗入边坡后形成均布荷载;降雨入渗受影响区域土体含水量均匀变化,经过时间t后的含水量为ω=6.5×10-7t+0.21;拟合总凝聚力和内摩擦角与含水量 的 关 系 式 为c=440ω2-459ω +141.2;φ′ =-11.0ln(100ω)+59.2。

图2 降雨入渗后的失稳边坡
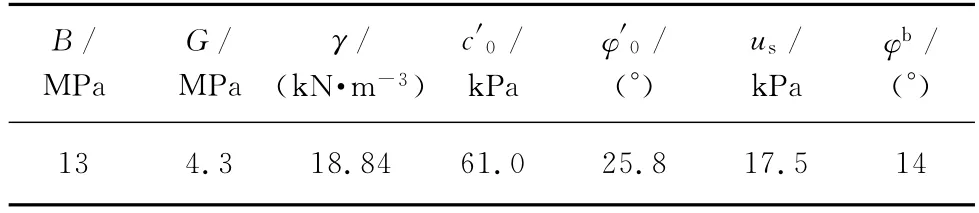
表1 非饱和土的物理力学参数
2.2 边坡动态安全系数数值计算
采用FLAC3D进行数值分析,对边坡进行计算网格划分,共划分6 672个节点、3 200个单元(如图4)。计算模型底面3个方向采用固定约束,2侧面和宽度方向受水平方向约束,自由面及坡面不受任何约束。
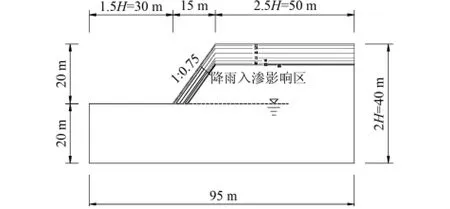
图3 降雨影响边坡计算几何模型
根据强度折减法的基本原理和降雨入渗条件下安全系数求解程序(图1),不断折减不同时间降雨条件下的强度指标c(ω)和(ω),直到边坡达到临界破坏时,塑性区将贯穿整个边坡,形成明显的滑动带,即为边坡最弱面或最危险面。降雨初始时刻按=61.0 k Pa、=25.8°进行强度折减分析,计算得到降雨影响区域如图4,得到相应的边坡安全系数Fs( t = 0)=1.73。随着降雨持续进行,按每12 h找到相应的边坡渐进破坏面和安全系数。当t=84 h,Fs( t = 84 h)=1.04,边坡即将破坏,此时将降雨间隔时间定为1 h,可得到比较高的精度。
随着降雨持续进行,土体吸湿不断向内发展,边坡形成渐进的破坏模式(图5)。当t=86 h,滑移面贯穿整个边坡,说明边坡已经破坏。边坡受降雨影响区域的土体参数及动态安全系数计算结果见表2,边坡吸湿后含水量增加20.1%,边坡就发生失稳破坏,此时边坡滑动面仍处于非饱和状态。根据工程边坡的重要性及要求,当t=84 h可以认为边坡将发生失稳,应及时采取相关措施防治。

图4 降雨影响的边坡计算FLAC3D模型

表2 边坡安全系数计算结果

图5 持续降雨入渗边坡的应变增量变化图
随着降雨持续进行,边坡土体抗剪强度指标和安全系数是一个动态变化过程,边坡各参数c(ω)、(ω)和Fs(ω)的降低变化情况如图6所示。图6反应了持续降雨条件下非饱和土边坡稳定性情况,降雨前阶段土体指标和安全系数的变化率越越大,降雨后阶段的参数变化率逐渐减小,直到边坡失稳破坏。持续降雨条件下,边坡安全系数的变化规律主要受土的凝聚力影响。

图6 参数c(ω)、(ω)和Fs(ω)随时间的变化率
3 结论
通过持续小强度降雨对非饱和土边坡稳定性的动态影响分析,可以得到如下结论:
1)建立了持续小强度降雨入渗条件下非饱和土边坡安全系数的定量关系式,将土体含水量引入到强度折减法中。
2)边坡降雨影响区域土体吸湿后,凝聚力和内摩擦角以及基质吸力都降低了,随着降雨持续进行,边坡土体抗剪强度指标和安全系数是一个动态变化过程,降雨前阶段土体指标和安全系数的变化率越越大,降雨后阶段的参数变化率逐渐减小,直到边坡失稳破坏。
3)以含水量作为抗剪强度的主要控制参量,通过强度折减法得到了持续降雨过程中边坡的渐进破坏面、动态安全系数和破坏时间,为持续的小强度降雨条件下土边坡的加固防护和失稳预测提供参考。
4)计算结果表明,持续小强度降雨条件下,边坡主要呈现吸湿过程,边坡的临界滑动面含水量仍处于非饱和状态。
[1]Fredlund D G, Rahar djo H.Soil mechanics f or unsaturated soils [M].New York:John Wiley and Sons,Inc.,1993.
[2]Fredlund D G,Xing A,Fredlund M D,et al.The relationship of the unsat urated soil shear strength to t he soil-water characteristic curve [J].Canadian Geotechnical Jour nal,1996,33(3):440-448.
[3]Fredlund D G.Unsat urated soil mechanics in engineering practice[J].Jour nal of Geotechnical and Geoenvironmental Engineering,2006,132(3):286-321.
[4]Au S W C.Rain-induced slope instability in Hong Kong[J].Engineering Geology,1998,51(1):1-36.
[5]Collins B D,Znidarcic D.Stability analyses of rainfall induced landslides [J].Jour nal of Geotechnical and Geoenvironmental Engineering,2004,130(4):362-372.
[6]Mohamed T A,Ali F H,Hashi m S,et al.Relationship bet ween shear strength and soil water characteristic curve of an unsaturated granitic residual soil[J].American Journal of Environmental Sciences,2006,2(4):142-145.
[7]Chu-Agor M L,Fox G A,Cancienne R M,et al.Seepage caused tension failures and erosion undercutting of hillslopes[J].Journal of Hydrology,2008,359(3/4):247-259.
[8]Huang M,Jia C.Strength reduction FEM in stability analysis of soil slopes subjected to transient unsaturated seepage[J].Co mputers and Geotechnics,2009,36(1/2):93-101.
[9]Oh W T,Vanapalli S K.Influence of rain infiltration on the stability of compacted soil slopes[J].Computers and Geotechnics,2010,37(5):649-657.
[10]吴宏伟,陈守义,庞宇威.雨水入渗对非饱和土坡稳定性影响的参数研究[J].岩土力学,1999,20(1):1-14.WU Hongwei,CHEN Shouyi,PANG Yuwei.Parametric study of effects of rain infiltration on unsaturated slopes[J].Rock and Soil Mechanics,1999,20(1):1-14.
[11]李萍,张毅,房明.土质高边坡的降雨渗流场数值模拟分析[J].建筑科学,2009,25(1):28-31.LI Ping, ZHANG Yi, FANG Ming.Numerical si mulation of seepage field of high soil slope under rainfall[J].Building Science,2009,25(1):28-31.
[12]李兆平,张弥.考虑降雨入渗影响的非饱和土边坡瞬态安全系数研究[J].土木工程学报,2001,34(5):57-61.LI Zhaoping,ZHANG Mi.Effects of rain infiltration on transient safety of unsaturated soil slope[J].China Civil Engineering Journal,2001,34(5):57-61.
[13]Dawson E M,Roth W H,Drescher A.Slope stability analysis by strength reduction [J].Geotechnique,1999,49(6):835-840.
[14]栗茂田,武亚军,年廷凯.强度折减有限元法中边坡失稳的塑性区判据及其应用[J].防灾减灾工程学报,2003,23(3):1-8.LUAN Maotian, WU Yajun, NIAN Yankai.A criterion f or evaluating slope stability based on develop ment of plastic zone by shear strength reduction FEM [J].Jour nal of Seismology,2003,23(3):1-8.
[15]Liu Z Z,Yan Z X,Duan J.Couple analysis on strength reduction theory and r heological mechanis m f or slope stability[J].Jour nal of Central Sout h University of Technology,2008,15(Sup1):351-356.
[16]杨庆,贺洁,栾茂田.非饱和红粘土和膨胀土抗剪强度的比较研究[J].岩土力学,2003,24(1):13-16.YANG Qing,HE Jie,LUAN Maotian.Co mparative study on shear strength of unsaturated red clay and expansive soils[J].Rock and Soil Mechanics,2003,24(1):13-16.
[17]Çokça E,Tilgen H P.Shear strength-suction relationship of compacted Ankara clay [J].Applied Clay Science,2010,49(4):400-404.
[18]汤有光,郭轶锋,吴宏伟,等.考虑地表径流与地下渗流耦合的斜坡降雨入渗研究[J].岩土力学,2004,25(9):1347-1352.TANG Youguang,GUO Yifeng,WU Hongwei,et al.A preli minary study of rainfall infiltration on slope using a new coupled surface and subsurface flow model[J].Rock and Soil Mechanics,2004,25(9):1347-1352.

