基于复合学习算法的配电网理论线损计算模型
邓敏,刘克文,王宇飞
(1.北京电力建设公司,北京市,100024;2.中国电力科学研究院,北京市,100192)
0 引言
目前基于机器学习的各种理论线损计算方法已逐渐成为配电网理论线损计算的重要手段[1-4],其思路是先将理论线损计算问题抽象成多元回归问题,进而利用机器学习算法求解多元回归问题。但是随着研究的深入上述方法逐渐暴露出一些问题:一方面,文献[1-2]仅使用神经网络作为理论线损计算方法,因而难以克服神经网络固有的易陷于局部极小值、计算误差大等缺陷;另一方面,文献[3-4]虽然利用遗传算法(genetic algorithm,GA)优化神经网络训练参数提高了理论线损计算精度,但GA本身迭代次数多、运算复杂,降低了计算方法的实用性。
针对配电网理论线损精确计算,本文利用复合学习算法(hybrid learning algorithm,HLA)设计理论线损计算模型,HLA由广义回归神经网络(generalized regression neural network,GRNN)和粒子群算法(particle swarm optimization,PSO)复合而成。HLA方法将理论线损计算问题抽象成多元回归问题(multi regression problem,MRP),并利用GRNN对各已知理论线损线路的数据训练得到理论线损计算模型,以其求解待测线路的理论线损,HLA引入 PSO优化GRNN的训练参数选取,以改善理论线损计算模型的计算精度。经算例验证,基于HLA的配电网理论线损计算方法具有更高的计算精度。
1 复合学习算法
1.1 广义回归神经网络及训练参数
GRNN是一种基于径向基函数的回归型神经网络[5]。GRNN具有局部非线性逼近能力强、收敛速度快、自学习能力强等特点,GRNN由径向基传输层和线性输出层组成,如图1所示。

图1 广义回归神经网络模型Fig.1 GRNN construction
GRNN依靠径向基函数完成输入向量到线性输出层输入向量的变换,图1中‖dist‖是径向基距离,用于控制映射输出。通常采用Gauss函数作为径向基函数,设函数K为Gauss函数,x为输入向量,x'为Gauss函数中心,σ为Gauss函数的平滑因子,用以控制函数径向作用范围,e=2.718 3,如公式(1)所示。

σ是GRNN最重要的训练参数,σ的取值过大,易造成GRNN欠拟合,σ取值过小,易造成GRNN过拟合。
1.2 粒子群算法
PSO是一种高效的群智能优化算法,拥有较强的全局寻优能力和较快的收敛速度[6]。PSO的核心思想是对目标问题构造n维解空间,在解空间中初始化1个包含若干粒子的种群,每个粒子代表目标问题的1个n维可行解,并且每个粒子具有各自的速度。每个粒子根据自身飞行经验和群体飞行经验调整飞行轨迹,向最优点(目标问题最优解)靠拢,直至种群中的某个粒子达到最优点,或PSO算法达到种群最大迭代次数终止。
1.3 复合学习算法工作过程
HLA由GRNN和PSO复合而成,其中GRNN通过对样本集的训练得到学习模型,以求解目标问题。由1.1节可知,训练参数σ将直接决定GRNN的计算精度,故而HLA使用PSO动态地搜索训练参数σ的最优值,以改善GRNN的计算精度。HLA工作过程如图2所示。

图2 复合学习算法工作流程Fig.2 Work process for hybrid learning algorithm
2 配电网理论线损计算
2.1 理论线损计算的数学模型
配电网理论线损通常由线路的有功供电量P、无功供电量Q、线路长度L、配电变压器总容量T等因素决定,可以视为一个具有“多输入、单输出”特性的复杂函数。因此基于HLA的理论线损计算方法将理论线损计算问题抽象成多元回归问题(multi regression problem,MRP)[7],将配电网理论线损的若干影响因素作为MRP的输入向量,将理论线损值y作为MRP的输出向量,利用HLA对配电网各线路的历史数据进行训练学习得到理论线损计算模型。对于某待测线路i的理论线损计算,只需将其若干影响因素输入到理论线损计算模型即可得到高精度结果,如图3所示。
由图3可见,求解配电网理论线损主要由“数据预处理”和“求解MRP”组成,其中“数据预处理”将理论线损计算问题抽象成MRP。数据预处理由2个步骤组成,分别是“特征选择”和“样本集构造”。
步骤1特征选择。通过特征选择确定MRP的输入向量和输出向量。配电网台区实际情况复杂,各种用户类型和线路类型同时存在,并且影响理论线损的因素很多,故而需要选择对理论线损计算影响最大的几类因素。经反复实践发现有功供电量P、无功供电量Q、线路长度L、配电变压器总容量T共4个因素对理论线损计算影响巨大,选其作为MRP的输入向量。
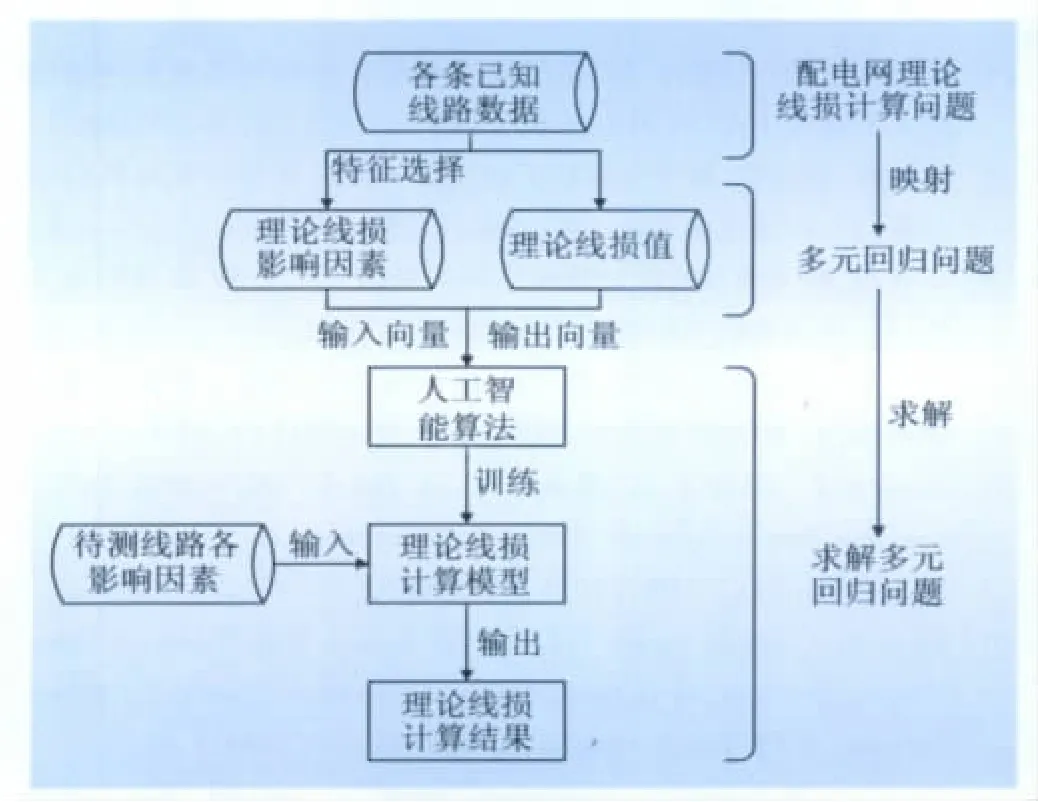
图3 利用复合学习方法求解理论线损工作流程Fig.3 Work process for theoretical line loss calculation by HLA
步骤2样本集构造。样本集中每条记录有6维,第1维是线路编号,第2~5维分别是无功供电量P、有功供电量Q、线路长度L、配电变压器容量T,第6维是线路理论线损值。进而将样本集分为训练样本集和测试样本集,训练样本集用以供HLA生成临时计算模型,测试样本集用于修正临时计算模型误差以得到最终高精度计算模型。
2.2 复合学习算法设计
HLA设计主要是GRNN和PSO的参数设定。
理论线损计算包括4维输入向量、1维输出量,因而GRNN的网络结构为4-4-1。径向基函数是Gauss函数,平滑因子σ最优值由PSO迭代搜索。
PSO通过适应度函数F控制GRNN计算误差。设某条线路i的理论线损实际值yi,^yij是根据粒子j的训练参数所得线路i的理论线损计算值,该条线路i的误差为

若测试样本包含m条待测线路,则对应PSO中j点坐标的测试样本平均计算误差θj可由式(3)得到,PSO的适应度函数F定义如式(4)所示。

F(j)的值越小,说明根据当前粒子j的训练参数所得HLA模型计算误差越小。本文设定F的阈值ε=0.08,当F≤ε时迭代结束。
公式(5)~(7)是PSO迭代公式,用以更新粒子速度和位置。公式(5)~(7)中,V为粒子速度,S为粒子位置,pbest为粒子的历史个体最优位置,gbest为种群的历史最优位,k为迭代次数。
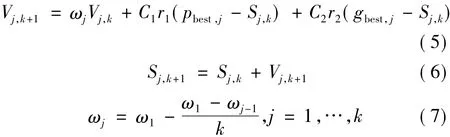
3 算例验证
为充分说明基于HLA的配电网理论线损计算方法的优势,采用文献[1-4]的标准数据设计实验。标准数据采集自某低压台区时间跨度为1个月的长期理论线损,并以能量损耗表示理论线损。该台区有68条线路,并且理论线损已知,现以这68条线路数据构造样本集,选择第1~60条线路数据组成训练样本集,第61~68条线路数据组成测试样本集。每条线路样本均有6维数据,分别为线路编号、月有功供电量 P(×104kW·h)、月无功供电量Q(×104kW·h)、配电变压器总容量T(kVA)、线路总长度L(km)、理论线损y(×104kW·h)。同时选用BP神经网络、RBF神经网络、GA优化的BP神经网络、GRNN共4种方法做横向对比实验,实验结果见表1。表1中理论线损的单位是“×104kW·h”,HLA的适应度函数曲线如图4所示。
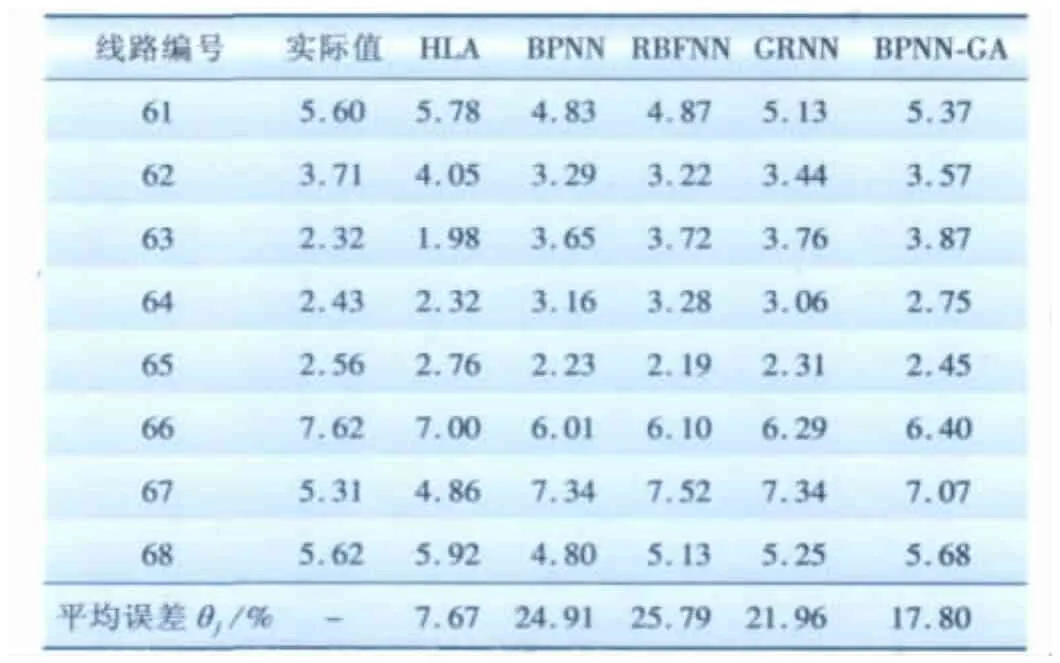
表1 测试样本集实验结果Tab.1 Experimental results of sample set
由表1可见,HLA方法的计算误差要远小于另外4种方法,其原因在于:一方面,BPNN、RBFNN、GRNN 3种方法未采用任何训练参数优化措施,导致误差偏高,虽BPNN-GA利用GA优化其训练参数,但GA自身易陷于局部极小点,计算误差仍较高;另一方面,HLA利用PSO动态地搜索GRNN最优训练参数,并且PSO的全局寻优能力优于GA,因而HLA方法的计算误差较小。
如图4所示,随着PSO迭代,适应度函数值逐渐下降。从第1代至第10代适应度函数值下降明显,第10代之后适应度函数值变化趋于平缓,最终在第91代适应度函数值收敛于最小值0.076 7,这充分说明了PSO前期全局收敛能力强,后期局部收敛能力强的特点。

图4 适应度函数曲线Fig.4 Fitness function curve
综合上述分析,HLA方法在配电网理论线损计算中有较高实用价值。
4 结语
本文提出一种基于复合学习方法HLA的配电网理论线损计算方法。通过PSO动态搜索GRNN最优训练参数,克服了原有智能化理论线损计算方法中普遍存在的训练参数选取困难的问题,改善了理论线损计算精度。通过横向对比实验证明,与传统方法相比基于复合学习算法HLA的配电网理论线损计算方法具有较高的实用价值。
[1]姜惠兰,安敏,刘晓津,等.基于动态聚类算法径向基函数网络的配电网线损计算[J].中国电机工程学报,2005,25(10):35-39.
[2]文福拴,韩祯祥.基于分群算法和人工神经元网络的配电网线损计算[J].中国电机工程学报,1993,13(3):41-50.
[3]辛开远,杨玉华,陈富.计算配电网线损的GA与BP结合的新方法[J].中国电机工程学报,2002,22(2):79-82.
[4]李秀卿,赵丽娜,孟庆然,等.IGA优化的神经网络计算配电网理论线损[J].电力系统及其自动化学报,2009,21(5):87-91.
[5]Keem S Y,Chee P L,Abidi I Z.A Hybrid ART-GRNN Online Learning Neural Network With a e-Insensitive Loss Function[J].Neural Networks,2008,19(9):1641-1646.
[6]Ko C N,Chang Y P,Wu C J.A PSO Method With Nonlinear Time-Varying Evolution for Optimal Design of Harmonic Filters[J].Power Systems,IEEE Transactions on,2009,24(1):437-444.
[7]Chen S. Multi-output Regression using a Locally Regularized Orthogonal Least-squares Algorithm [J].Vision,Image and Signal Processing,IEE Proceedings,2002,149(4):185-195.

