塔高对冷却塔风振系数的影响分析
侯宪安,柯世堂,马峰,梁娅莉
(1.中国电力工程顾问集团西北电力设计院,西安市 710075;2.南京航空航天大学土木工程系,南京市 210016)
0 引言
冷却塔是典型的钢筋混凝土高耸旋转薄壳结构,模态耦合性强,对风荷载的作用十分敏感,风荷载是冷却塔结构设计的控制性荷载之一[1-2]。随着冷却塔塔高及直径的增加,结构的柔性也随之增大,自振频率相应降低。由于自然界脉动风的能量主要集中在低频区域,因此对于柔性更大的超大型冷却塔而言,结构风致动力响应也将更为显著。
目前,国内外冷却塔结构设计规范[3-5]在考虑脉动风对冷却塔结构的影响时通常采用拟静力法,即采用平均风压乘以风振系数或采用阵风风压乘以动力放大系数后作为等效静风荷载用于冷却塔结构静力分析。影响冷却塔结构风振响应数值和分布特性的因素很多,从本质上可以分为2类:一是结构自身的特性,如结构的自振频率、阻尼比等;二是来流的特性,如所在场地的地貌特征、结构表面的风压分布、周边建筑物的干扰效应等[6]。
国内冷却塔设计规范[3-4]在定义冷却塔的风振系数时较为简单,仅仅考虑了地貌特征因素,忽略结构自身特性等其他重要影响因素,同一地貌类型场地上的不同冷却塔采用相同的风振系数,在考虑风的作用时采用10 min平均风压乘以风振系数后作为等效静风荷载。
尽管国内冷却塔的最大塔高已从20世纪70年代的100 m左右,增大到目前接近甚至突破200 m,但几十年来国内电力行业普遍采用的冷却塔结构设计规范关于风振系数的取值规定,几乎没有变化,仅风振系数取值适用塔高范围从“适用于塔高150 m以下”扩展到“适用于塔高165 m以下”。
德国冷却塔设计导则[5]在考虑风的作用时,考虑了地貌特征和结构特征(自振频率、喉部直径等),采用3 s阵风风压乘以风作用动力放大系数后作为等效静风荷载。研究表明,冷却塔不同的部位对风激励的响应并不一致,而且风振系数数值上差异还比较大,整座冷却塔乘以一个统一的风振系数或动力放大系数而得到的所谓等效静力风荷载,与风对结构的等效激励存在差异。
本文针对3座体型比例相近而塔高不同的双曲线冷却塔,采用考虑背景、共振以及背景和共振分量之间交叉项的风致响应计算方法,分别计算各自的风振系数数值及其分布特征,研究冷却塔塔高对风致动力作用的影响程度,得到各自对应的等效静力风荷载。本文研究结论可为冷却塔的结构设计和抗风安全性研究提供参考。
1 研究对象
为了对比研究冷却塔不同高度对其风振系数的影响,本文选择了3座体型比例相近而塔高不同的冷却塔作为研究对象,其主要特征尺寸如表1所示。
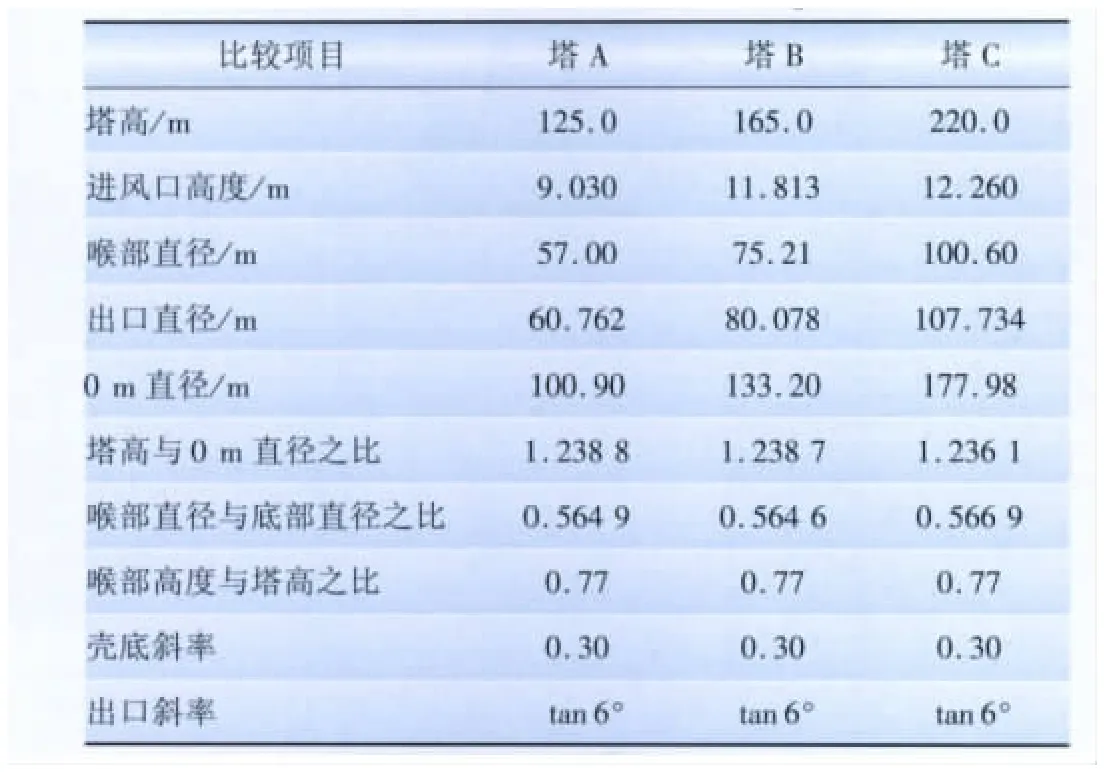
表1 研究对象冷却塔主要特征尺寸Tab.1 Main feature size of cooling towers
本文采用有限元分析软件考察风致动力系数与自振频率的关系,对研究对象分别建模,进行了模态分析,提取了其前10阶自振频率,结果如表2所示。
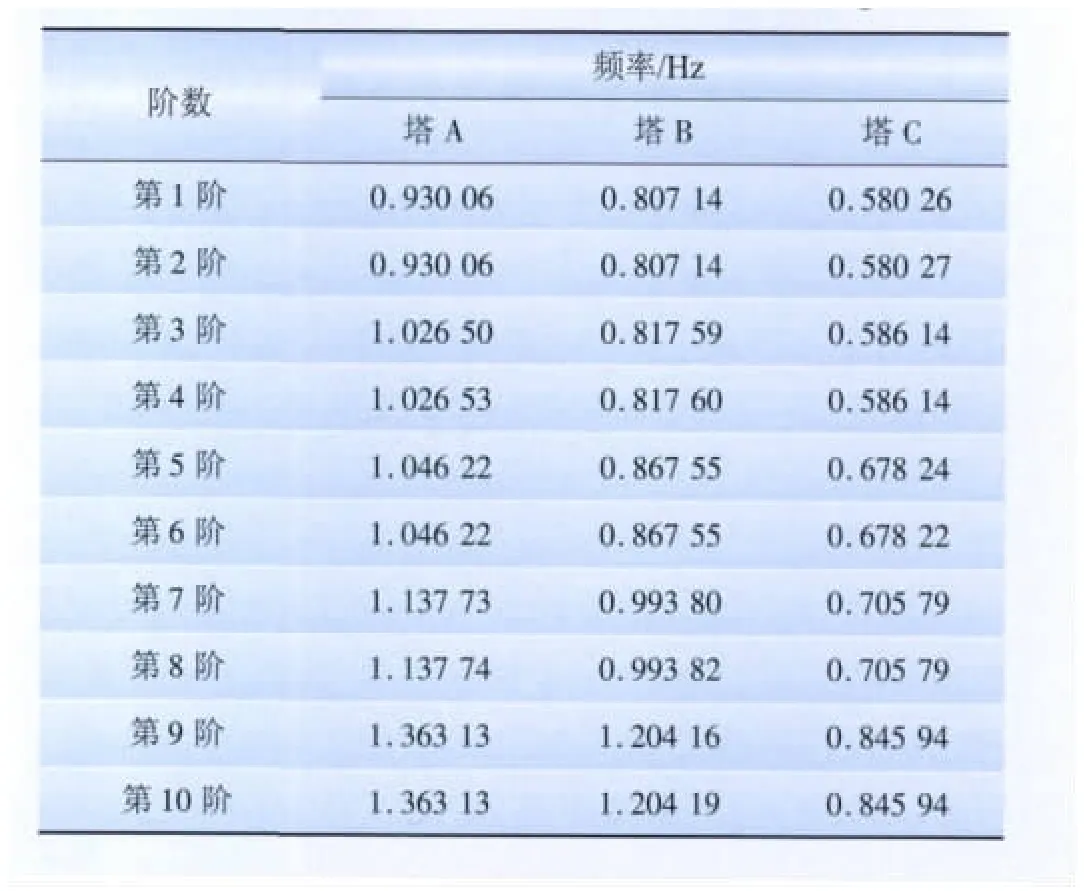
表2 冷却塔前10阶自振频率Tab.2 The front 10 natural frequencies of cooling towers
2 风振一致耦合分析方法
柔性结构在风荷载激励下的随机动力响应方程可表达为
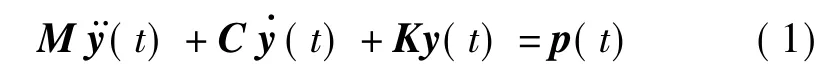
使用模态叠加原理,式(1)可表示为
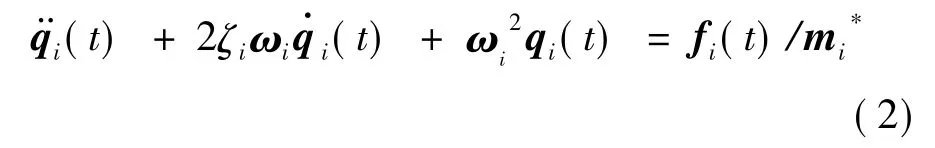
式中:qi(t)表示第i阶模态的广义位移向量;fi(t)表示第i阶模态的广义力向量。
对于柔性结构的风致动力响应来说,高阶模态的共振响应通常可以忽略,这样,动态位移可以表示为

式中:Φ为振型矩阵;q(t)表示模态广义位移向量;φi为第i阶振型向量;qi,b(t)为仅包含准静力贡献的第i阶背景位移响应向量;qi,r(t)为仅包含共振效应贡献的第i阶共振位移响应向量;yb,n(t)为包含所有模态准静力贡献的背景响应向量;yr,m(t)为仅包含共振效应贡献的前m阶模态共振位移响应向量。
2.1 传统的频域求解方法
(1)采用平方和开根号(square root of sum of squares,SRSS)方法来组合背景和共振分量,可以表示为
式中:σt、σb,n、σr,m分别代表了响应向量 y(t)、yb,n(t)、yr,m(t)的均方差。其中背景分量可作为准静力响应,采用荷载-响应相关方法(load response correlation method,LRC)来求解,共振分量采用惯性风荷载方法来计算。不足之处,这一方法不能考虑背景和共振之间的模态耦合项,也不能很好地考虑共振模态之间的耦合项。
(2)求解总脉动响应的组合方法为
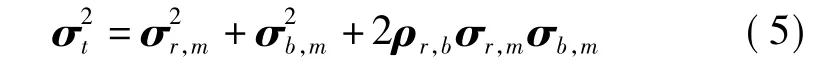
式中:背景分量σb,m是前m阶背景位移向量yb,m(t)的均方差;ρr,b为背景分量和共振分量之间的相关系数,即

从式(5)可以看出,背景分量仅仅包含前m阶模态准静力贡献,相应地,背景和共振分量之间的交叉项也是仅仅包含前m阶模态的贡献。
2.2 改进的频域求解方法
根据式(5),可将脉动风总响应均方差精确地表述为
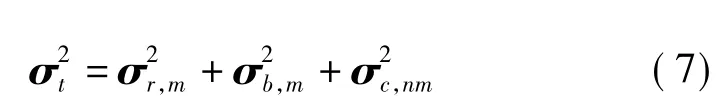
式中σc,nm代表前n阶背景分量和前m阶共振分量的交叉项。
与传统方法最大的不同在于式(7)能考虑所有模态的准静力贡献,前m阶共振模态之间的耦合效应,n阶背景模态和前m阶共振模态之间的交叉项。
2.3 风振一致耦合分析方法原理
背景分量可以基于外荷载激励的协方差矩阵,并采用LRC原理进行精确求解。借鉴这一思路,提出广义恢复力协方差矩阵、共振恢复力协方差矩阵和耦合恢复力协方差矩阵这一概念,统一引入LRC方法来求解共振和交叉项分量,进而使得相应的等效静力风荷载的求解有了理论基础。这样,式(7)变成

式中:I为影响线矩阵;Cppt为广义恢复力协方差矩阵;Cppb为外荷载协方差矩阵;Cppr共振恢复力协方差矩阵;Cppc为耦合恢复力协方差矩阵。
这样,耦合恢复力协方差矩阵的表达式可以进一步简化为

求解式(9)时,可先分别求解背景、共振和耦合恢复力协方差矩阵,然后基于LRC方法获得各响应分量和等效静力风荷载分量[7-8]。
3 结果分析
本文基于风振一致耦合分析方法,采用B类地貌某电厂冷却塔风洞试验测得的表面脉动风荷载数据作为激励输入,阻尼比为0.05,考虑所有阶模态的背景响应和前50阶模态的共振响应,分别计算得到3座研究对象冷却塔的风振系数,结果如图1所示。

图1 节点风振系数分布Fig.1 Distribution of wind vibration coefficients at nodes
3.1 典型节点风振系数的三维分布
从图1可看出:在相同的激励下,单个冷却塔不同部位的风振系数并不统一,数值起伏较大;在平均风压分布较小的区域(如在环向40°和120°处),风振系数往往较大,但由于这些区域的风压绝对值不大,对结构响应的影响不大;再对比3个不同塔高的冷却塔风振系数分布等值线图发现,风振系数数值沿子午向和环向变化较大,但存在一个共同点——均在环向40°和 120°出现最大值。
3.2 风振系数沿高度方向的分布
分别计算了纬向平均风振系数分布、0°子午线上风振系数分布、70°子午线上风振系数分布,结果如图2所示。从图2可看出:无论是平均风振系数还是典型部位的风振系数,3座冷却塔均表现出相同的趋势——冷却塔越高,风振系数越大;3个塔沿着子午向高度的增大均是先增大、再减小、最后再增大的变化规律;不同标高处各点的风振系数数值差别较大;由于0°子午线区域的来风比塔两侧及尾区脉动小,所以与70°子午线相比,0°子午线各点的风振系数要小。
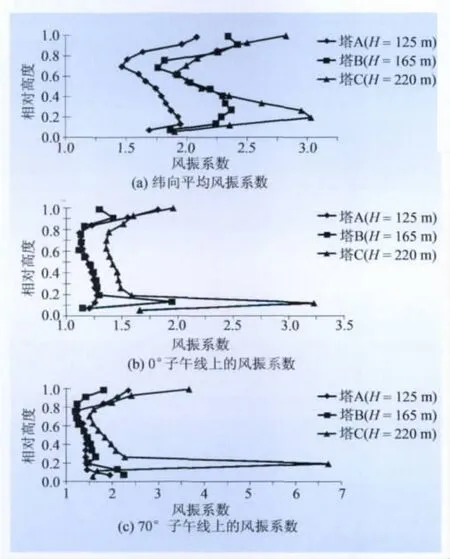
图2 子午向风振系数分布曲线Fig.2 Distribution curves of meridian wind vibration coefficients
分别计算了喉部标高纬向风振系数分布、子午向平均的风振系数沿纬向的分布、子午向平均风振系数等效风压沿纬向的分布,结果如图3所示。从图3可看出:从等效风压曲线上看尽管某些区域的风振系数数值相当大,但对曲线的影响并不如风振系数的变化反应那么大,不过也不能忽略。例如图3(c)中塔C在70°左右的等效风压系数几乎达到3.5,比规范给出的风振系数高出近2倍,在结构设计时对其影响应予以重视。
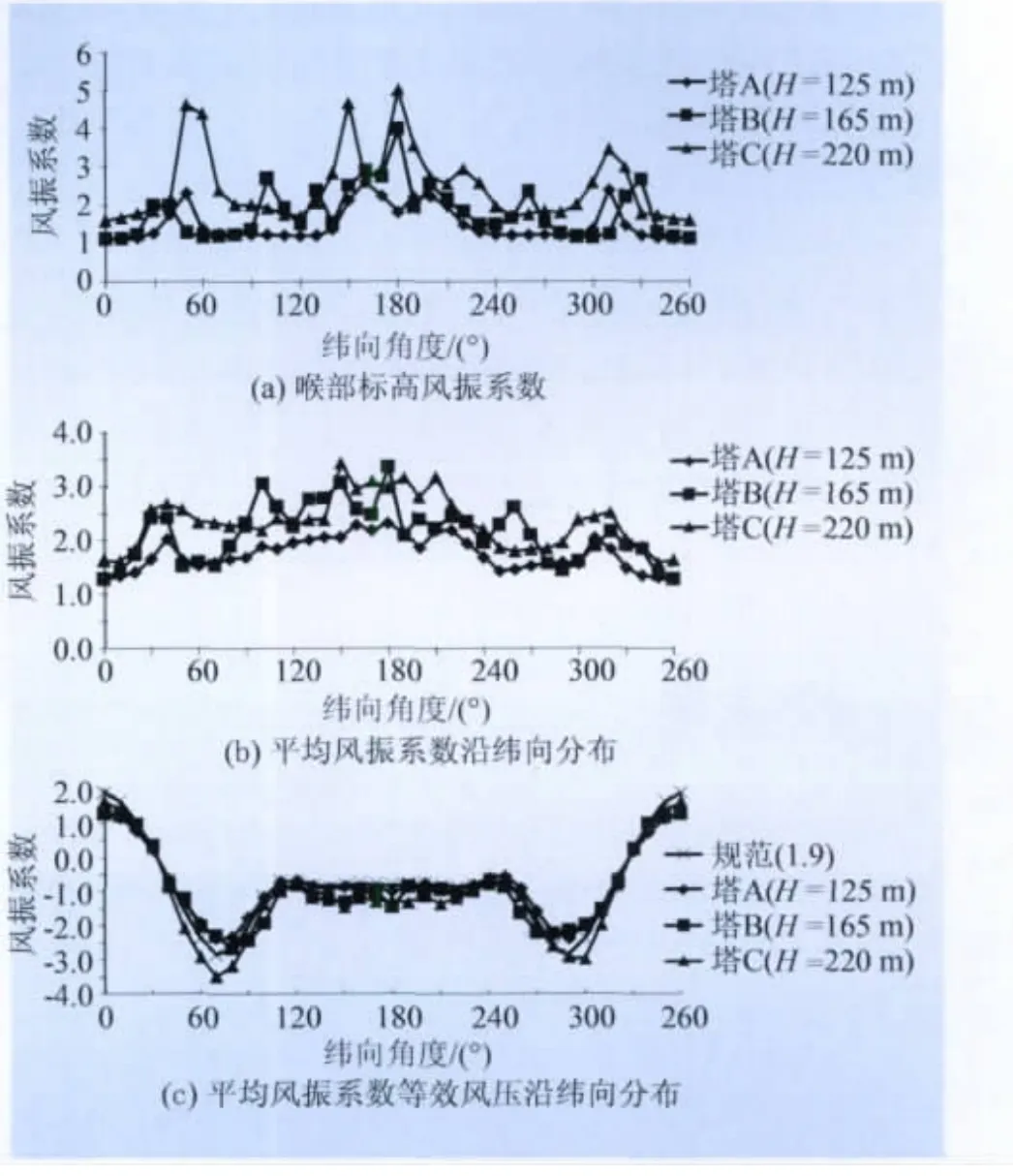
图3 环向风振系数分布曲线Fig.3 Distribution curves of loop wind vibration coefficients
3.3 动力放大系数
按照德国冷却塔设计导则 VGB-R610Ue[5]给出的方法,分别计算了3座冷却塔的动力放大系数,结果如表3所示。表3所示动力放大系数计算结果显示,3座塔的动力放大系数从塔A到塔C呈现两头大的趋势。

表3 研究对象冷却塔动力放大系数Tab.3 Dynamic amplification coefficients of cooling tower
4 结论
(1)冷却塔不同部位的风振系数并不统一,数值上差别还比较大,故规范在考虑风振影响时全塔采用单一的风振系数不合理。
(2)冷却塔风振系数受塔高的影响明显,较高的冷却塔风振系数相应也大。分析其原因,冷却塔风振系数与结构的自振频率有关,体型相同的条件下,结构自振频率越低,越接近自然界风脉动的频率,风振系数越大。
(3)3座研究对象冷却塔中,塔A基频最高,直径最小,结构环向刚度相对较大,从理论分析和风振计算结果看,其受到的风振影响应该最小。但按德国规范计算得到的动力放大系数却是3座冷却塔中最高的,由此可以看出,尽管德国冷却塔设计导则VGB-R610Ue考虑了基频、塔顶风压、喉部直径等因素的影响,但可能仍不够完善。
[1]张彬乾,李建英,阎文成.超大型双曲冷却塔双塔干扰的风荷载特性研究[J].流体力学试验与测量,2003,17(S):93-97.
[2]刘若斐,沈国辉,孙炳楠.大型冷却塔风荷载的数值模拟研究[J].工程力学,2006,23(6):177-184.
[3]DL/T 5339—2006火力发电厂水工设计技术规范[S].北京:中国电力出版社,2006.
[4]GB/T 50102—2003工业循环水冷却设计规范[S].北京:中国计划出版社,2003.
[5]VGB-R 610Ue Structural design of cooling towers technical guideline for the structural design,computation and execution of cooling towers[S].VGB-Guideline,2005.
[6]柯世堂.大型冷却塔结构风效应和等效风荷载研究[D].上海:同济大学,2011.
[7]柯世堂,葛耀君.基于一致耦合法的大型博物馆结构风致响应精细化研究[J].建筑结构学报,2012,33(2):23-29.
[8]柯世堂,侯宪安,陈少林.大型冷却塔结构多目标等效静风荷载分析[J].电力建设,2012,33(9):6-10.

