基于谱回归判别分析的LPP算法*
杨 凡,张银玲,牛 静(浙江师范大学 数理与信息工程学院,浙江 金华321004)
人脸识别中的维数约简是一个关键问题,流行的维数约简方法包括主成分分析PCA(Principal Component Analysis)[1]、线性判别分析 LDA(Linear Discriminant Analysis)[2]、局部保持投影 LPP(Locality Preserving Projection)[3]等。LPP被认为是一种有效的维数约简方法,它在保持数据集的局部结构的同时,通过邻接图来确认流形结构模型的一种线性变换,它已经成功应用于许多邻域[4]。LPP的目的是寻找一个投影矩阵,在投影后,两个样本点的距离最小,然而,它却忽略了样本间的判别信息。参考文献[5]中,Yu提出了判别局部保持投影DLPP(Discriminant Locality Preserving Projection)算法,他在 LPP算法中加入了判别信息来提高识别率。但是,在DLPP算法计算过程中,需要解决密度矩阵的特征分解问题,这给时间和内存方面带来了非常高的计算成本。参考文献[6]中,Cai证明了LDA的空间复杂度为:O(mnt+t3),并且占用内存为:O(mn+mt+nt),其中m是样本的个数,n是类个数,t=min(m,n)。当m和n很大时,应用到较大的数据集上,几乎是不可行的。最近,谱方法作为一种有效的维数约简方法已经运用到人脸识别中。参考文献[6]中,Cai提出一个新的判别分析算法,即谱回归判别分析SRDA(Spectral Regression Discriminant Analysis)。通过使用谱图分析,SRDA将判别分析投射到回归框架上,它只需要解决一系列正则化的最小二乘问题,而不需要计算特征向量,节省了时间和内存的消耗,在计算方面明显地优于LDA算法。本文提出了一种新的改进算法——谱回归判别局部保持投影SRDLPP(Spectral Regression Discriminant Locality Preserving Projection)。其在LPP算法中加入了谱回归判别分析算法,这样可以避免解密度矩阵特征分解时带来的高昂的内存和时间的消耗。分别在Yale、Orl和扩展Yale_B人脸库上进行实验,实验结果表明,本算法优于其他算法。
1 算法介绍
1.1 LDA算法
线性判别分析LDA(Linear Discriminant Analysis)是从高维特征空间中提取出最具有判别能力的低维特征,以达到抽取分类信息和压缩特征空间维数的效果,投影后保证样本在新的子空间有最大的类间距离和最小的类内距离。算法思想如下:
假设对于一个 Rn空间有{xi}个样本分别为 x1,x2,…,xm,即每个 x是一个 N×M行的矩阵,假设有 C个类,则n1+n2+…+ni+…+nc=m。
样本类间离散度矩阵定义为:

样本类内离散度矩阵定义为:

LDA的目的是寻找一个变换矩阵W:

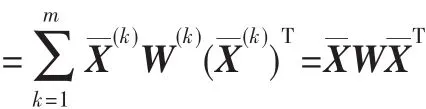


在过去的几十年中,有人提出各种各样的方法来解决这个问题(例如SVD、PCA+LDA等方法)[2,8-11]。谱回归判别分析算法思想来源于谱方法SR(Spectral Regression)。SR算法从根本上是基于回归和谱图分析[12]。SR能够有效地应用标记点和非标记点来发现数据内在的固有的判别式结构。这个图用于得到标记点和非标记点的学习响应。一旦得到响应,嵌入函数可以通过一般的回归模型得到。SR算法避免了解密度矩阵的特征分解问题。根据SR算法,CAI提出SRDA算法。
1.2 SRDA算法
为了有效解决LDA方程(4)的特征问题,利用如下定理:

定理1求特征方程(4)的解,从下列两步获得:



称为正则化,在统计学中有很好的研究。正则的最小二乘法同样被称为脊回归[13]。该算法是在图的谱分析之后对LDA的特征方程进行回归处理,因此称为谱回归判别分析,简记为SRDA。
1.3 SRDLPP算法
根据以上的分析可知,LDA的计算包括解密度矩阵的特征分解,这使得时间内存上都带来了很大的消耗。SRDA算法可以有效地节省时间和内存。受SRDA算法启发,本文提出一种改进的LPP算法:谱回归判别局部保持投影 SRDLPP(Spectral Regression Discriminant Locality Preserving Projection)。算法如下:
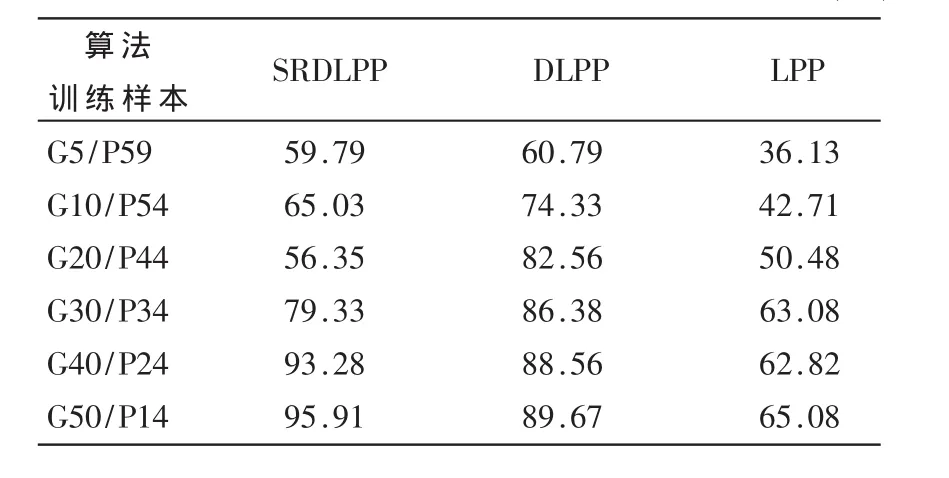
LPP的目的是寻找xi经过投影后在低维空间中对应的 点 yi,yi=aTxi。 Y=[y1,y2,…,ym], 是 一 个(d×m)矩 阵(d< W是对称的矩阵,最小化目标函数就是要确保当ai和aj距离很近时,yi和yj的距离也很近。 (1)创建邻接图:设G是表示m个顶点的图,每一个顶点代表一个数据点。W是对称的m×m矩阵,表示连接点i和j的权值为Wij。这里采用K邻域法构造权值矩阵W。 用 Nk(xj)表示 xi的 K邻域集。 在一定的约束条件下使得式(8)中y是最佳的,描述为: 那么a就是下列方程最小特征值问题对应的特征向量: (2)特征分解:计算特征方程(13)的解,可以从以下两步中获得: 根据定理1: ①求解特征问题式(11)得到y. 其中最优化的y是下列特征问题的最大特征向量 又因为存在一个线性函数:yi=aTxi 则特征方程(11)为: (3)正则化最小二乘问题:根据上面分析,最小化方程(14)可能是病态的,所以加入一个范数a: 找到 d 个向量 a1,…,ad∈Rn,aj=(j=1,…,c-1)。 设 A=[a1,…,ad],A 是 n×(c-1)变换矩阵,样本数据点可以嵌入 c-1维空间中:xi→yi=ATxi,A=[a1,a2,…,ad] y是样本点数据的d维表示,A是本文算法的转变矩阵。根据以上分析,在数据库上进行实验。 Yale人脸库共有165张人脸图像,每个人有11张的表情照片,归一化为32×32人脸图像。这些照片有戴眼镜、不戴眼镜、开心、悲伤等,共11种表情。Gp/Pq表示每人随机选取p张训练集人脸训练,q张测试集人脸测试。 每一个训练集选取(3,4,5,6,7,8)图像,例如:3 训练集表示训练图像共有45张人脸用来训练,剩余8测试集共120张人脸用来测试。为了确保实验结果的可靠性,每次实验重复20次,取平均识别率和时间消耗值,正则化参数a根据经验选择0.01。实验结果如表1、表2所示。表1、表2显示了Yale人脸库上的识别率和时间消耗,可以看出,本文算法的结果优于DLPP和LPP算法。DLPP需要计算密度矩阵特征分解问题,它占用更多的时间和内存;对于LPP来说,当训练数增加时,识别率下降;本文提出的算法最高识别率达到94.53%。表2表示每一次识别的平均时间,当训练样本数增加时,DLPP时间消耗越多。 表1 Yale人脸库识别率 (%) 表3 在ORL人脸库识别率 (%) 表4 在ORL人脸库上时间消耗 (s) ORL人脸库,共有40人,每人有10幅图像,这些图像包含表情和姿态变化。原图像的大小为112×92,在预处理阶段,统一归一化成32×32大小的人脸图像。随机选择每人(3,4,5,6,7,8)图像 集作为 训练,其他作为测试。例如:3训练集共120个人脸图像作为训练,余下7测试集共280个人脸图像作为测试。为了确保得到稳定的实验结果,每次实验重复20次。取平均识别率和平均时间消耗。实验结果如表3、表4所示。 DLPP 的 识别率优于本文提出的算法和LPP算法。但是它同时也消耗了大量的时间。计算平均数据集每一次所占用的时间消耗,最高的达到50 s。 扩展的Yale_B人脸数据库包含16 128幅人脸图像,共38类,9种姿态65种细节下进行,本文选择正面且所有的图片细节不同,每人得到64图片。所有人脸图片剪裁为 32×32像素,256灰度级。 特征(像素值)在[0,1]之间(除以256)。实验结果如表 5、表6所示。 表5 在扩展Yale_B人脸库识别率 (%) 表6 在扩展Yale_B人脸库上时间消耗(s) 表5、表6为在扩展的Yale_B人脸库上的识别率和时间消耗。可见,DLPP的识别率比较高,但是占用了太多的时间,平均识别一次所需要时间最高达到900 s。本文提出的算法最高识别率达到95.91%. 综合以上3个实验结果可知,本文提出的算法,在一定程度上提高了识别率,特别是时间消耗方面具有明显的优势,尤其是在数据集较大的情况下,优势越明显。 本文提出一种新的人脸识别算法——谱回归判别局部保持投影算法SRDLPP(Spectral Regression Discriminant Locality Preserving Projection)。它利用谱回归判别分析的思想加入到局部保持投影中。实验结果表明,虽然DLPP的识别率有较好的效果,但是由于它需要计算密度矩阵求解特征问题,占用了很大的时间和内存消耗,在实际运用中存在弊端。谱回归判别分析算法只需要解决一系列正则化的最小二乘问题,而不需要计算特征问题,这大大地节省了时间和内在的消耗。SRDLPP算法不仅提高了识别率而且时间和内存的消耗都比较少。分别在Yale、Orl及扩展Yale_B人脸库上进行实验,结果表明该算法具有高效的识别率、低的时间及内存消耗。 [1]MARDIA K V,KENT J T,BIBBY J M.Multivariate analysis[M].Academic Press,1980. [2]SWETS D L,WENG J Y,Using discriminant eigenfeatures for image retrieval[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(8):831-836. [3]He Xiaofei,NIYOGI P.Locality preserving projections[A].Neural Information Processing System[C].Vancouver:MIT Press,2003. [4]FOLEY D H,SAMMON J W Jr.An optimal set of discriminant vectors,IEEE Transactions on Computer,1975,C-24(3):281-289. [5]Yu Weiwei,Teng Xiaolong,Liu Chongqing.Face recognition using discriminant locality preserving projections[J].Image and Vision Computer,2006(24):239-248. [6]Cai Deng,He Xiaofei,Han Jiawei.SRDA:an efficient algorithm for large scale discriminant analysis[J].IEEE Transactions on Knavledge and Data Engineering,2008,20(1):1-12. [7]FUKUNAGA K.Introduction to statistical pattern recognition 2nd edition[M].Academic Press,1990. [8]TORKKOLA K.Linear discriminant analysis in document classification[C].Proceedings of IEEE ICDM Workshop Text Mining,2001. [9]HOWLAND P,PARK H.Generalizing discriminant analysis sing the generalized singular value decomposition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(8):995-1006. [10]YE J.Characterization of a family of algorithms for generalized discriminant analysis on undersampled problems[J].Journal of Machine Learning Research,2005(6):483-502. [11]FRIEDMAN J H.Regularized discriminant analysis[J].Journal of the American Statistical Association,1989,84(405):165-175. [12]CHUNG F R K.Spectral graph theory[M].AMS,1997. [13]HASTIE T,TIBSHIRANI R,FRIEDMAN J.The elements of statistical learning:data mining,inference,and prediction[M].New York:Springer-Verlag,2001.







2 SRDA嵌入到LPP中
3 实验结果与分析
3.1 Yale人脸库

3.2 ORL人脸库


3.3 扩展 Yale_B人脸库