小波去噪在超声多普勒信号处理中的应用⋆
梁 璐, 高国旺, 殷 光, 马桥斌
(西安石油大学光电油气测井与检测教育部重点实验室, 陕西西安 710065)
0 引言
去噪处理是信号处理中的一项重要内容,信号在产生、传输、接收等过程中因为受电噪声、传输噪声等的干扰对有用信号造成了污染,不利于进一步对信号进行分析与处理。现在信号去噪的方法有很多,如维纳滤波、卡尔曼滤波等。在超声多普勒流量计的研制过程中,需要对回波信号特征的提取与分析,因此,信号去噪这一步为进一步获得有用信息显得尤为重要。本文采用小波变换对信号进行去噪处理。小波变换是在傅里叶变换的基础上发展起来的一种处理信号的时频分析方法,它具有多分辨率分析的特点,而且在时、频域都具有表征信号局部特征的能力,是一种窗口大小固定不变,但其形状可变、时间窗和频率窗可变的时频局部化分析方法[4]。即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,很适合于探测正常信号中夹带的瞬态反常现象并展示其成分,所以被誉为分析信号的显微镜[9]。1994年D.L.Donoho和I.M.Johnstone在小波变换的基础上提出了小波阈值去噪的概念,并证明了此方法可在Besov空间中得到其他任何线性形式不可能达到的最佳估计[1],由于小波变换中阈值去噪方法的出众的表现,使得它得到了广泛的推广与应用,阈值法去噪不仅能够达到很好的噪声抑制作用,而且可以很好地保留反映原始信号的特征尖峰点,具有很好的去噪效果。但由于硬阈值函数的不连续,软阈值函数中函数中估计小波系数与带噪信号的小波系数之间存在着恒定的偏差的缺陷,限制了它的进一步应用。为克服这一缺点,本文在超声波信号的处理中采用了一种改进后的阈值函数对其进行去噪,通过硬阈值、软阈值函数及改进后的阈值函数进行图形仿真、信噪比和均方误差的对比可看出此方法的优越性。
1 超声多普勒流量测量原理
声学中,当声源与观察者之间的距离随时间缩短时收听到的频率高于声源发出的频率;反之,收听到的频率低于声源频率。声源发出的频率与观察者听到的频率之间的频率差称为多普勒频移,它的大小取决于两者之间的相对运动速度,这种现象称为多普勒效应[3]。
利用多普勒法测量时,超声波传感器的激励方式分别为:单载频脉冲波激励、连续正弦波激励等。本文中采用连续正弦波信号激励方式,用一对斜探头垂直对称安装在管道外侧(如图1所示),发射探头产生的连续波超声信号经声楔和管壁进入运动中的流体,并被随流体一起运动的固体悬浮颗粒、气泡等可以散射超声波信号的物质散射而进入接收探头。通过测定流体中运动粒子散射声波的多普勒频移,完成流量检测。

图1 多普勒流量测量示意图
超声多普勒流量测量示意图如图1所示,超声波在被测流体中的传播速度为c,u为悬浮颗粒在流体中的流速,f1为发射超声波的频率,f2为接收的超声波信号的频率,Δf为多普勒频移,其中θ1为发射的连续超声波束与流速之间的夹角,θ2为散射超声波束与流速之间的夹角。通常情况下θ1=θ2。
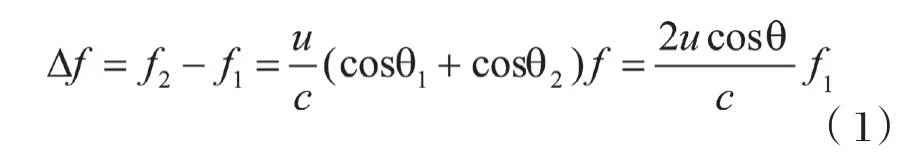
被测管道中的流体的流速为:
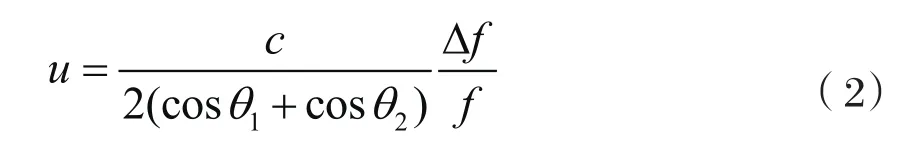
实验当中由于所获得的信号噪声较大,有用信号成为了小信号,对于后续为获得频偏信息的频谱分析等信号处理工作造成了一定影响,因此下面将采用了小波分析的去噪方法对超声波回波信号进行去噪处理。
2 小波去噪
2.1 小波去噪原理
工程中通常采集上来的数据信号,由于采集工具和工作环境的影响,采集到的信号大多数是含有噪声的降质信号,要想对信号分析出理想的结果来,降噪成为信号处理中的必要条件。传统的去噪方法有线性滤波和非线性滤波去噪法,它的不足在于使信号变换后的熵增高、无法形象地表征非平稳信号的特性,并且无法得到信号的相关性,而小波变换可以很好地克服这一缺点,达到很好的信号去噪效果。在小波去噪的方法中阈值去噪是一种简单实用的方法,它的原理是利用了小波分解后的各层系数中模值大于和小于某阈值的系数分别处理,再对处理完的小波系数进行反变换,重构出经过去噪后的信号。
假设采集的信号为:
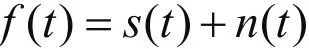
其中s(t)为原始信号,n(t)为服从N(0, δ2)的高斯白噪声,对f(t)进行离散采样,得到n点离散信号f(n),n=0, 1, 2, N-1;为了简单对噪声进行说明,我们认为n(t)为高斯白噪声N(0, 1)。其小波变换为:

Wf(j, k)为小波系数,由于上式计算小波系数比较复杂,工程应用中通常采用小波变换的递归实现方法[10]:
在15份访谈资料中,药费虚高、去人性化和缺少共情是大医院为人诟病的地方,而曼巴扎仓在这些方面却比大医院做得好,更有公益心和人性化。在曼巴扎仓,病人的医疗费人均50元,住院部提供的病房每间每月60元。对于那些贫困无靠和孤寡老人,医药、住宿全部予以豁免,且无偿提供燃料和食物。这就是为什么在医保覆盖90%以上藏区人口的情况下,人们还涌向曼巴扎仓治病的原因。
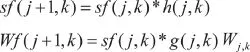
其中,sf(0, k)为原始信号,sf(j, k)为尺度系数,wf(j, k)为小波系数,h和g分别为尺度函数和小波函数对应的低通和高通滤波器,从而得到小波重构公式如式(4)所示:
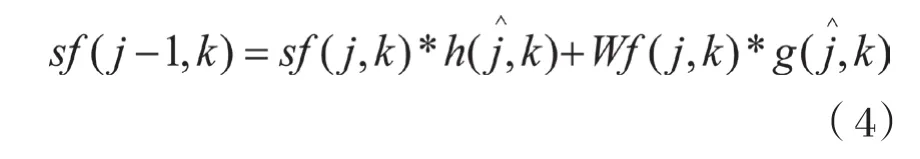
2.2 小波阈值去噪
Donoho在小波变换的基础上提出了小波阈值去噪的概念,它的去噪基本思想是: 当小波系数Wj,k小于某个临界阈值时, 认为这时的小波系数主要是由噪声引起的,要将其归为零; 当Wj,k大于这个阈值时, 认为这时的小波系数主要是由信号引起的, 则把这一部分的Wj,k直接保留下来 (硬阈值方法), 或者按某一个固定量向零收缩 (软阈值方法 ), 然后用新的小波系数进行小波重构, 从而得到去噪后的信号,具体步骤如下:
1)小波分解。选择小波基函数和小波分解的层次,对含噪信号进行小波变换得到一组小波系数Wj,k;
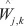
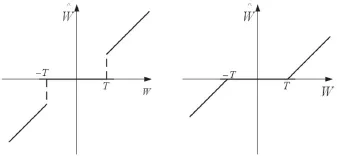
图2 估计小波系数的软硬阈值函数
在实际应用当中我们发现,影响去噪效果的关键不仅与阈值和阈值函数的选取有关,小波分解的层数对于去噪效果也有十分重要的影响。以往在使用小波阈值去噪时通常都是根据经验预先设定一个分解层数,但依据仿真结果来看,对不同的信号,在信噪比不同的情况下分解层数的选取直接影响到去噪的效果,当分解层数过多时,对所有各层小波系数都进行阈值处理,会造成有用信号信息的丢失,反而使信噪比下降,而且计算工作量也大为增加;当分解层数过少时,导致不能有效地去除噪声,信噪比不能得到很大提高。因此,确定一个合理的分解层数对去噪也是必要的,通常在实际应用中选取3~5层。
3 改进后的小波阈值函数去噪
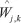
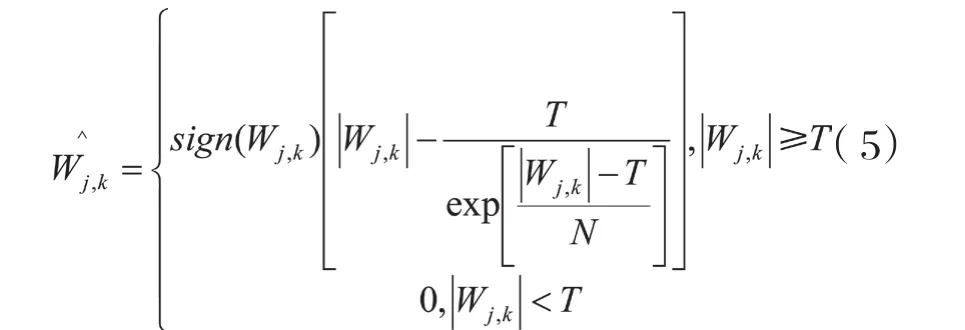
式中N为正常数。
当阈值T极小,且当N→∞时,式(5)为:
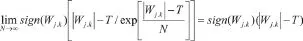
接近于软阈值。
在选择阈值时,Donoho提出的阈值的选择应满足:
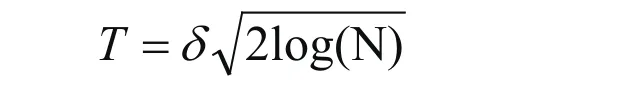
其中,δ是噪声标准方差,N为信号长度。但是由于此阈值在各个尺度固定不变,但噪声在各个尺度上都有分布,因此本文中将阈值取为:
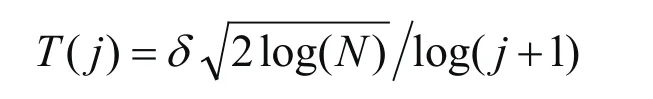
其中,j为分解尺度,N为信号长度。随着尺度j的增加,阈值T(j)逐渐减小,该特性符合噪声在小波变换各尺度上的传播特性相一致。
4 仿真研究

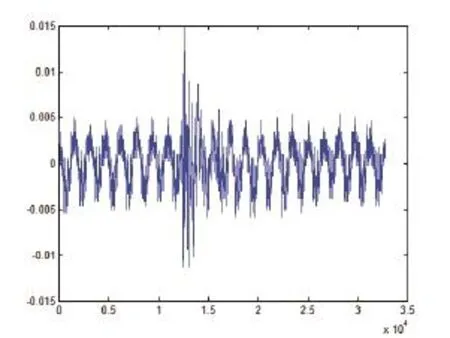
图3 采集到的超声多普勒回波信号
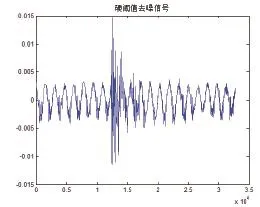
图4 硬阈值去噪
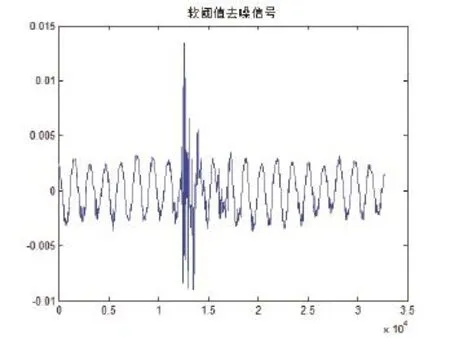
图5 软阈值去噪
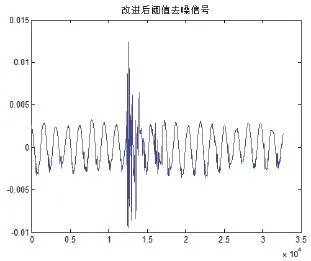
图6 改进后的阈值函数
对比软、硬阈值函数的仿真结果的信噪比与均方误差如表1所示。
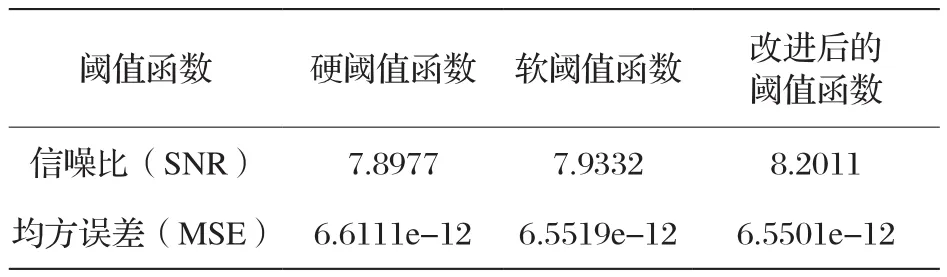
表1 3种阈值函数的信噪比及均方误差对比
由以上仿真图示可以看出改进型阈值函数较软硬阈值函数对于超声回波信号的去噪效果明显,且无论是从信噪比还是均方误差来看改进型阈值函数均优于软硬阈值函数。
5 结论
通过分析小波阈值去噪中软、硬阈值函数,本文采用了一种改进型的阈值函数,并将其应用到对超声多普勒流量计中回波信号的去噪处理中,通过仿真实验的结果明显可以看出,改进阈值函数有很好的可行性与有效性。从信噪比和均方误差来看,改进阈值函数的信噪比较其他方法大,均方误差本文所采用的改进法较软、硬阈值函数有所改进。
[1]张维强,宋国乡.基于一种新的阈值函数的小波域信号去噪[J].西安电子科技大学学报,2004,31(2):296-299.
[2]朱高中,王艳红.一种改进的小波阈值法在信号消噪中的研究[J].继电器,2007,35(18):41-45.
[3]冯若.超声手册[M].南京:南京大学出版社, 1999.
[4]张俊哲.无损检测技术及其应用[M].2版.北京:科学出版社,2010.
[5]周伟,桂林,周林,张家祥.MATLAB小波分析高级技术[M].西安:西安电子科技大学出版社,2006.
[6]岳钊,牛文成.小波分析在超声波传感器系统特征信号预处理中的应用[J].南开大学学报,2005,38(2):5-9.
[7]付炜,许山川.一种改进的小波域阈值去噪算法[J].传感技术学报,2006,19(2):534-540.
[8]乔飞,杨小军,马岸英.基于小波分析的多普勒弱信号检测方法[J].探测与控制学报,2008,30(1):48-52.
[9]郭晓霞,杨慧中.小波去噪中软硬阈值的一种改良折衷法[J].智能系统学报,2008,3(3):222-225.
[10]徐明耀.有限群导引(上册)[M].北京:科学出版社,1999.

