二次规划问题的新型时滞投影神经网络的稳定性分析

陈珊珊 楼旭阳

江南大学轻工过程先进控制教育部重点实验室 江苏 214122

0 引言

众所周知，二次规划是非线性规划中比较简单的一类，由于较容易求解，所以很多方面的实际问题都可以抽象成二次规划的模型去求解，例如在运筹学中，它被广泛用于经济调度，合理分配，计划决策等问题。

传统解决二次规划问题的方法过程复杂，计算时间长，使得其在大范围优化中的使用受到限制。神经网络具有大规模并行处理和分布式存储等特性，在高效运算方面具有更多优势。1986年，Hopfield和Tank首先提出将神经网络用于解决线性规划问题。近年来，建立神经网络来解决二次规划问题的研究发展迅速。Chen和Fang通过使用惩罚参数，提出了解决凸二次规划问题的时滞神经网络，得到了平衡点稳定的时滞稳定裕度。但是由于使用了惩罚参数，这种神经网络只能得到近似解。Liu，Cao和Wang提出一种时滞Lagrange网络来求解二次型规划问题，通过确定时滞间隔来保证时滞神经网络在最优点的渐进稳定性，但Lagrange乘子的存在，使得状态变量有所增加，导致了网络规模的扩大。Yang和Cao提出一类用于解决二次规划问题的时滞投影神经网络，这种模型不但没有包含Lagrange乘子和惩罚参数，而且用来求解二次规划问题也十分有效。但是，这种模型只考虑了部分神经元存在时滞的情况。

考虑到时滞的普遍存在性，本文在Yang和Cao的研究基础之上进行了改进，提出一类所有神经元皆存在时滞的投影神经网络模型。同时，利用Gronwall不等式和Halanay不等式给出了全局指数稳定性的证明。

1 问题描述

考虑如下二次规划问题：

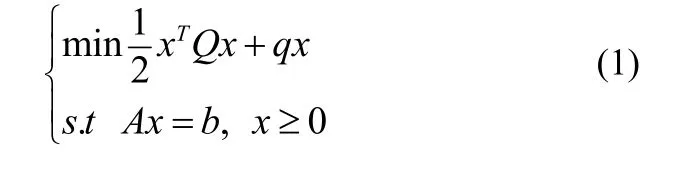
其中：Q∈Rn×n为正定或半正定矩阵，q∈Rn，A∈Rm×n为行满秩矩阵，b∈Rm，且假设可行域Ω=｛x∈Rn｝为非空集合。

文献【4】提出如下时滞投影神经网络来解决问题(1)：

其中α＞0恒成立，τ≥0表示传输延时。PΩ：Rn→Ω是一个投影算子，其定义如下：

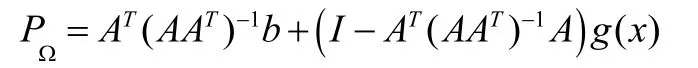
其中

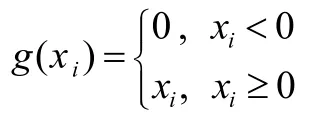
在本文中，我们对模型(2)加以改进，提出一个所有神经元皆存在时滞的投影神经网络来求解问题(1)：

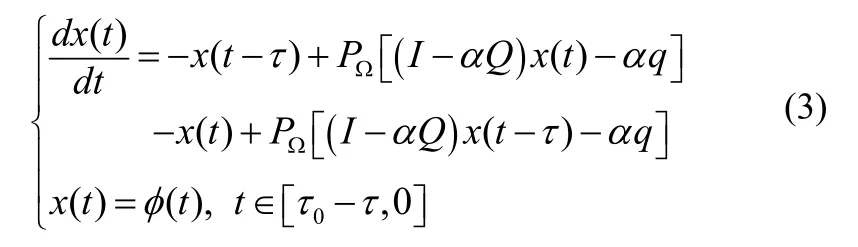
设Ωe为模型(3)中平衡点的集合，Ω*=Ωe是问题(1)中最优解的集合。可见，当且仅当x*是模型(3)的平衡点时，x*是模型(2)的平衡点，从而x*是问题(1)的最优解。所以，我们就有Ω*=Ωe。为了分析模型(3)的稳定性，我们引入下列的定义和引理。

定义1 如果由任意初始点x0出发的轨迹都满足：

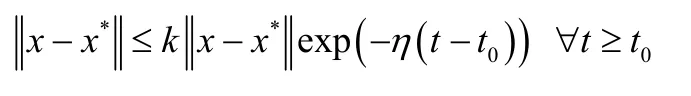
其中k和η是独立的恒定常量，那么就称这个系统在平衡点x*处是全局指数稳定的。

引理1(Gronwall不等式)设X(t)和Y(t)在［t0,+∞）上是非负连续的函数，如果

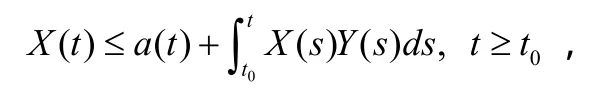
则

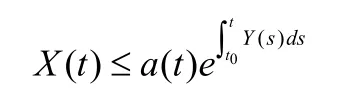
引理2(Halanay不等式) 令a＞b＞0，ν(t)为在［t0-τ,t0］上非负连续的函数且满足下列不等式：

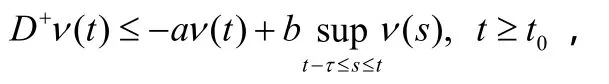
其中τ是一个非负常数，则存在常数λ＞0满足下列不等式：

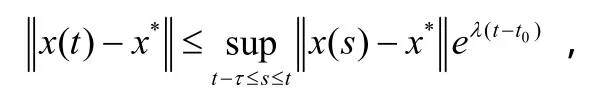
其中λ是方程λ=a-beλτ的惟一解。

2 主要结果

在这一节中，我们将讨论模型(3)的全局指数稳定性。定理1 如果任意给定一个初始值满足下列关系式：

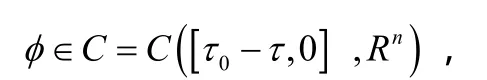
那么，就存在一个惟一的连续函数x(t)在区间［t0,∞）上满足模型(3)。

证明 令

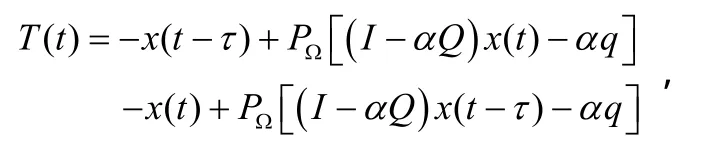
则模型(3)演化为：

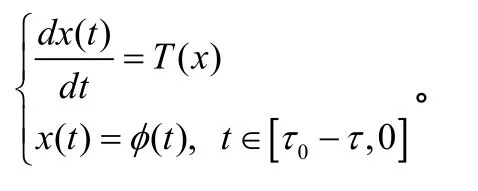
由于函数g(⋅)，PΩ(⋅)，T(⋅)是局部Lipschitz连续的，由微分方程解的存在性定理得，模型(3)存在一个解x(t)，其在［t0,T0）上满足x(t0)=φ。

因为x(t)∈Rn，于是我们可以得到：

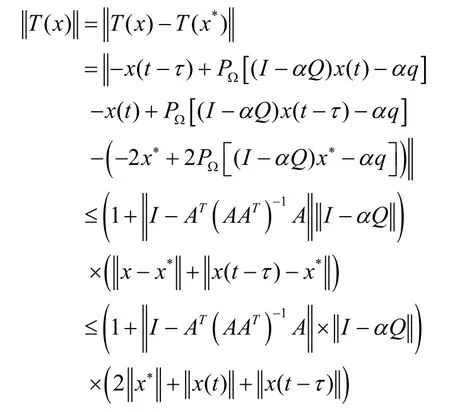
在区间［t0,t］（t0＜t）上，对模型(3)中的第一个式子两边同时求积分，得到：

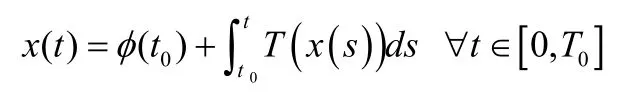
且x(t)=φ(t),-τ≤t ≤0。

所以：

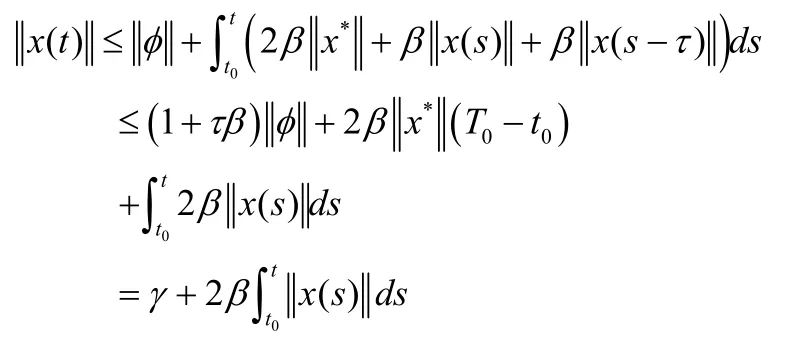
根据引理1，可以得到：

因此，解x(t)在[0,T0）上是有界的。

根据微分方程连续性法则，我们得到模型(3)在区间［τ0,+∞）上存在惟一连续解。

定理证毕。

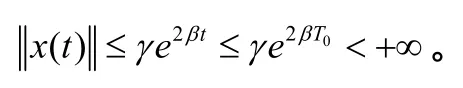
证明 设x*是模型(3)的一个平衡点，则有

x*=PΩ[（I-αQ）x*-αq] ，

从而可得：

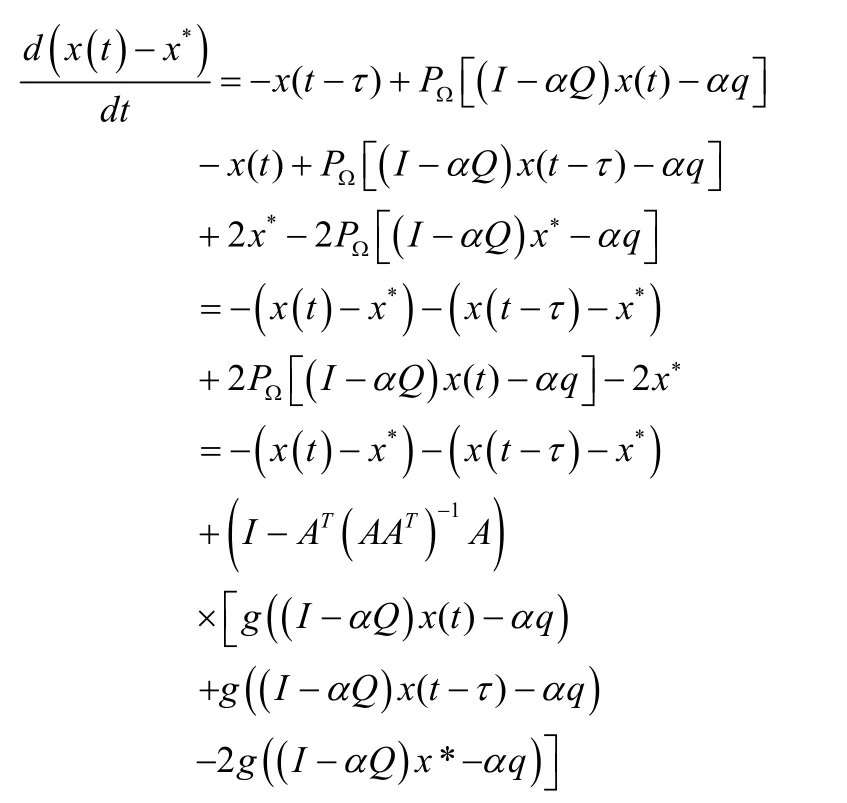
两边取范数得：

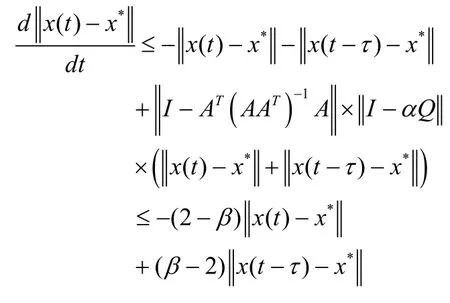
根据引理2，可以得到：

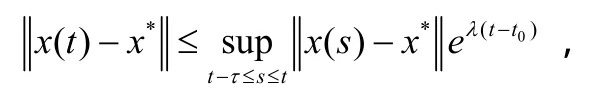
其中λ是方程λ=a-beλτ的唯一解。所以，模型(3)是全局指数稳定的。定理证毕。

注：当且仅当x*是模型(3)的平衡点时，x*是问题(1)的最优解。也就是说，任意x0∈Ω，模型(3)的解x(t,x0)指数收敛于问题(1)的惟一最优解。

3 仿真示例

为了说明所提出的时滞投影神经网络在解决二次规划问题中可行性和有效性，我们给出下面的仿真例子。

考虑如下的二次规划问题：

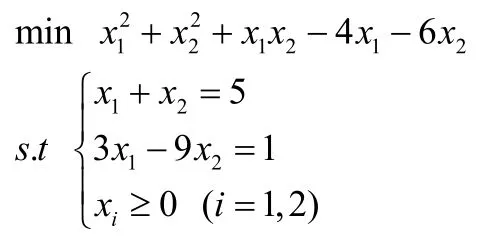
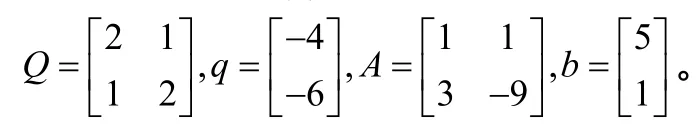
易知该问题对应(1)中的参数如下：

该问题最优解为x*=(3.8335,1.1667)T，取τ=0.5，α=1，分别利用模型(2)、模型(3)来求解此二次规划问题，在10个随机初始条件下，所有解的轨迹均收敛至最优解x*。仿真结果如图1、图2所示。利用模型(3)时，可以算出β=1，满足全局指数稳定的条件。

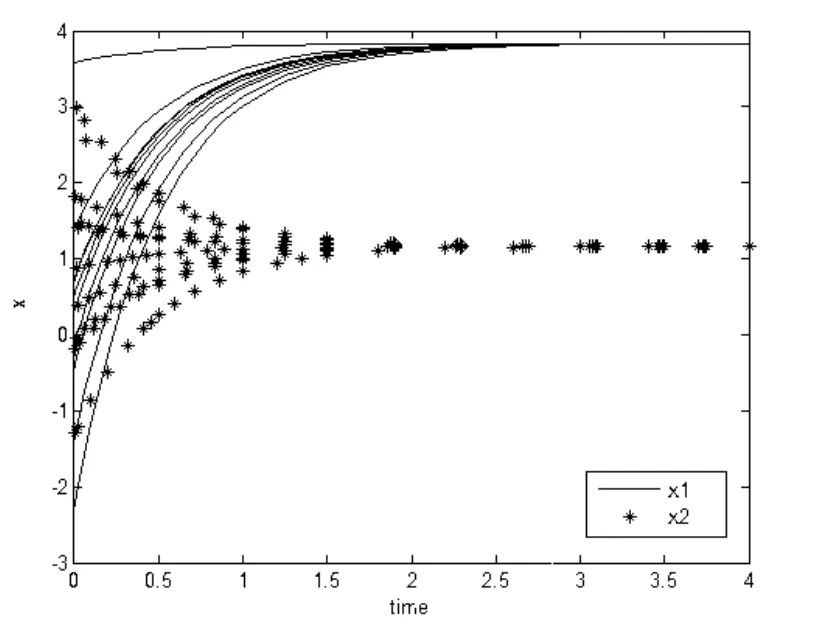
图1 利用模型(2)得到的时间响应曲线

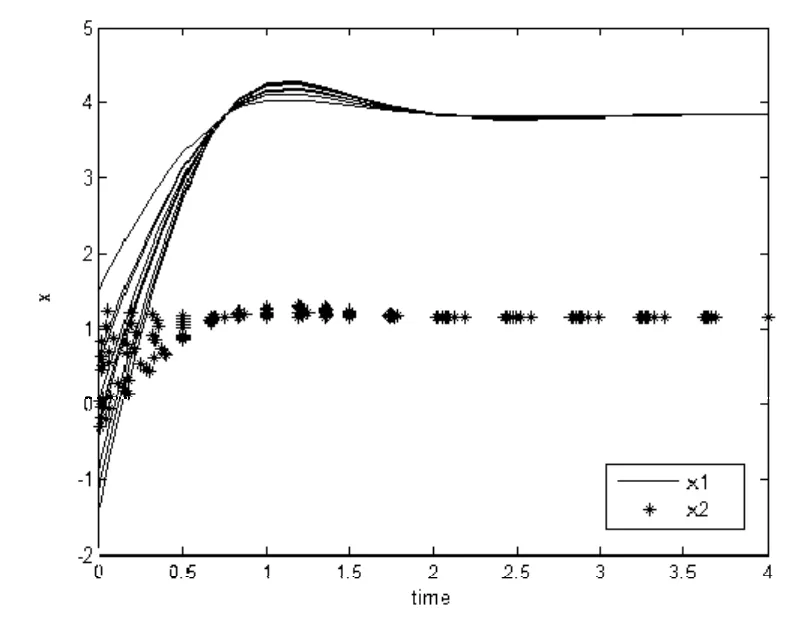
图2 利用模型(3)得到的时间响应曲线

从图中我们可以看出，模型(2)的1x和2x在接近3秒的时候才趋于稳定，而模型(3)在2秒左右就开始趋于稳定，即模型(3)比模型(2)的求解速度更快，并且具有很好的稳定性。

4 结论

本文提出了一种新型的时滞投影神经网络，用于解决二次规划问题。对所提网络模型的全局指数稳定性进行了详细的分析。数值实例说明了所提网络模型具有结构简单，求解速度快以及便于硬件实现等特点。

[1] 于春田,李法朝.运筹学[M].北京：科学出版社.2006.

[2] 朱继忠,徐国禹. 有功安全经济调度的凸网流规划模型及其求解[J].控制与决策.1991.

[3] 胡欣悦.基于任务分解结构的虚拟企业利益分配机制[J].计算机集成制造系统.2007.

[4] 戴道明.基于市场细分的定价与批量问题的联合决策[J].系统工程.2008.

[5] Hopfield J J,Tank D W.Simple neural optimization networks： An A/D convert[J].IEEE Transaction on Circuits and Systems.1986.

[6] Chen Y H,Fang S C.Neurocomputing with time delay analysis for solving convex quadratic programming problems[J].IEEE Transaction on Neural Networks.2000.

[7] Liu Q S,Wang J,Cao J D.A delayed Lagrangian network for solving quadratic programming problems with equality constraints[J].Lecture Notes in Computer Science.2006.

[8] Yang Y Q,Cao J D.Solving quadratic programming problems by delayed projection neural network[J].IEEE Transaction on Neural Networks.2006.

[9] 杨永清.神经网络优化方法及动态特性分析[D].南京：东南大学.2007.

[10] 廖晓昕.稳定性的理论、方法和应用[M].武汉：华中科技大学出版社.2002.

[11] 王林山.时滞递归神经网络[M].北京：科学出版社.2008.