基于分数阶Fourier变换的正交多载波水声通信系统研究

王逸林，陈韵，殷敬伟，蔡平，张艺朦

（哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001）

1 引言

21世纪被称为是海洋的世纪，各国将资源开发的目光转向蔚蓝色的海洋，而水声通信技术则是海洋资源开发中的关键技术。不同于无线信道，水声信道被看作为缓慢时变的相干多途信道[1]，具有时间、频率双弥散的特点，且能量的传播损失随距离和频率的增加而增大，因而导致水声信道多途效应严重和通信频带资源的稀缺。一般情况下，可用的通信频带范围只有几千赫兹[2]。这些不利因素严重制约着水声通信技术的发展。

分数阶 Fourier变换(FRFT, fractional Fourier transform)是一种新兴的时频分析工具，其之所以引起研究人员的重视，是因为它具有很多传统Fourier变换所不具备的性质。分数阶 Fourier变换实质上是一种时频变换[3]，建立了分数阶域(u域)与时域的联系。与传统Fourier变换相比，分数阶Fourier变换更适合处理非平稳信号，尤其是 chirp类信号。因为分数阶Fourier变换可以理解为chirp基分解，所以它对于以线性调频(LFM)信号为广泛应用的雷达、声纳信号处理领域有着很高的应用价值。目前分数阶Fourier变换被应用于数字水印技术[4]，合成孔径雷达[5]，模式识别[6]和通信技术中，其中文献[7,8]提出一种适用于无线信道的多载波通信方案，通过在收发两端同步自适应搜索最佳分数阶Fourier变换阶次以实现接收信号具有最小均方误差来应对信道的衰落问题，取得了良好的效果。然而水声信道与无线信道巨大的差异性使得这样的方案无法直接应用于水声通信中，因此开发一种适合于水声信道且能够高速、可靠、稳定的传输信息的通信方案具有重要的意义。

正交频分复用(OFDM)[9～11]技术具有较高的通信速率和频带利用率，但是对多普勒效应引起的载波偏移和相位噪声十分敏感，并且当某些子载波处于信道深度衰弱频点时，性能会有急剧地下降[12]。因此，本文针对以上问题，提出基于分数阶Fourier变换的正交多载波水声通信方案。该方案采用正交的线性调频(LFM)信号作为通信子载波，因为LFM信号是宽带非平稳信号，在兼顾通信速率的前提下，有效地抑制了通信信道对载波信号深度衰落的影响。同时，LFM信号较正弦信号具有较大的多普勒容限[13]，因而本方案也具有较强的抗多普勒效应的能力。宽带信号的高处理增益使得相较于窄带系统更加适合于复杂的低信噪比环境进行工作。本通信方案最高通信速率可达3.6kbit/s，相较于文献[14]通信速率有较大提升，经过大量的仿真实验和湖试实验证明了本方案的有效性与可靠性。

2 分数阶Fourier变换理论

如果将传统的 Fourier变换看成是将时间轴旋转π/2到频率轴，那么分数阶Fourier变换就可以看成是将时间轴旋转任意角度到分数阶域，建立起时域与分数阶域的联系[3]。因而分数阶Fourier变换是传统Fourier变换的一种推广，是Fourier变换的一种特殊形式[15]。分数阶Fourier变换表达式被定义为

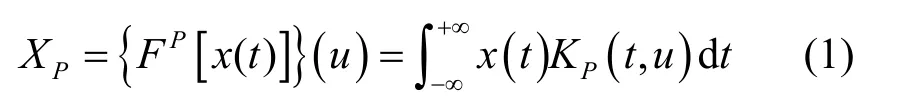
由分数阶Fourier变换的旋转特性可知，p阶分数阶 Fourier逆变换即为-p阶的分数阶 Fourier变换，表达式写为

下面介绍分数阶Fourier变换的一条重要性质，尺度变换特性：

尺度变换特性说明原函数在时间尺度上发生了变化，则变换象函数在u域尺度同时也发生了变化，且变换阶次即时频面旋转角度同时也发生了变化，一般可应用于信号受多普勒效应影响的处理。

离散分数阶 Fourier变换(DFRFT)有多种实现方式，目前大致主要分为3类：分解型[16]、线性组合型[17]和直接采样型[18]。本文主要采用Ozaktas在文献[16]中提出的改进型的分解型算法。这种离散化算法满足酉性，计算结果近似于连续分数阶Fourier变换，且采用FFT的方法加以实现，因而计算复杂度不高，计算量为O(NlogN)，使得实时计算成为可能。

3 基于FRFT的正交多载波水声通信系统实现

传统的OFDM技术，其主要思想是将原串行的高速数据流，并行的分配到N个相互正交的子载波上去，形成N个低速的并行独立传输的数据流，所得子载波数据流符号周期比原数据流符号周期扩大了N倍，有效地对抗了多途信道的时延扩展，并且这N个子载波相互正交，频带相互重叠，有效地提高了系统的频带利用率。

然而，水声信道是缓慢时变的相干多途信道，其信道冲激响应函数的幅频特性具有“梳状滤波器”的结构[1]，相间出现“通带”和“止带”，某些“止带”还会形成深陷的零点。当OFDM的某些子载波处于这种深陷的零点时，即形成深度的频率选择性衰落，并且水声信道所形成的这种“止带”的间隔与水层深度及厚度有关。一般来说，均匀层浅海信道平均止带间隔较宽，约为 100～300Hz的宽度，而对于负梯度水层的止带间隔却只有几十赫兹的宽度。因此，在通信频带本来就比较窄的水声信道中密布着这样的止带，这对于OFDM系统在水声信道中的性能有着较大的影响。另一方面，当通信系统存在较大多普勒频偏的情况下，OFDM系统中子载波的正交性会遭到破坏，形成严重的子载波间干扰(ICI)，此时无论如何提高系统的发射功率都不会改善系统的性能，形成所谓的“地板效应”[12]。

因此，本文提出采用相互正交的 LFM 信号作为子载波，以分数阶 Fourier变换作为调制解调方法的正交多载波通信系统。图 1给出了基于 LFM基和基于正弦基的OFDM系统的差别，从时频面上看主要是宽带的基信号取代了窄带基信号，LFM信号作为一种宽带信号，其能量分布在一定的带宽之内，能够有效应对深度频率选择性衰落信道，而且LFM 信号本身具有较大的多普勒容限结合分数阶Fourier变换的尺度变换特性，使其具有较强的抗多普勒效应的能力，对多普勒补偿算法要求较低甚至可以不用补偿，大大简化了系统复杂度，提高了系统的性能。

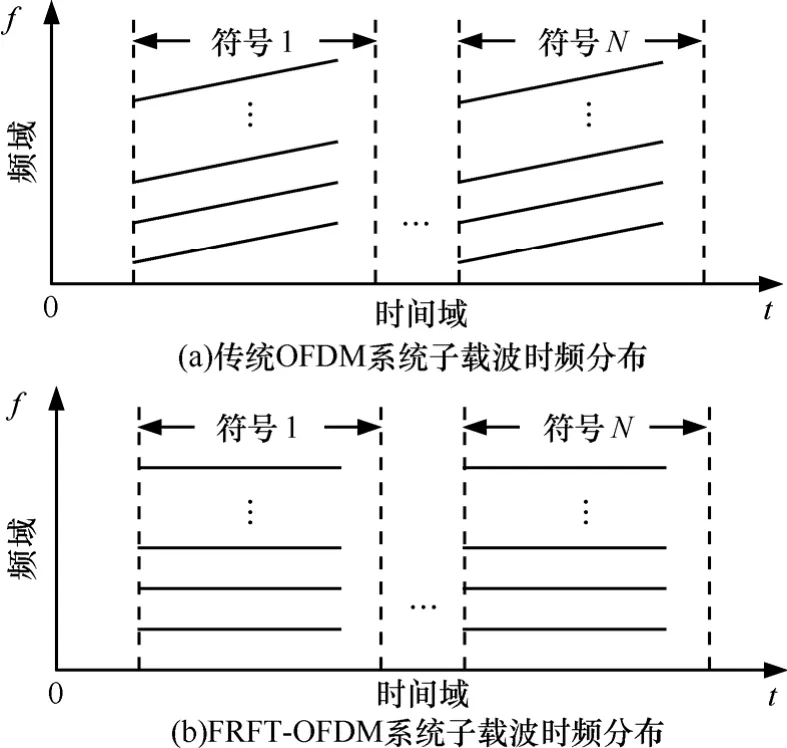
图1 FRFT-OFDM系统与传统OFDM系统载波时频分布对比

具体要做的研究包括：分析思想政治教育接受目的与思想政治教育接受效果之间的关系；厘清思想政治教育接受的“工具性”目的和“价值性”目的；研究思想政治教育接受目的的生成条件；通过实证调查分析总结当前思想政治教育接受目的存在的问题及原因。借鉴哲学解释学所倡导的“主体间性”原则、“对话”关系、“实践智慧”等理念，彰显思想政治教育接受活动的“价值性”目的等。

由式(6)得到这样一个结果，分数阶变换域中一组间隔为sinα/T的冲激函数，其分数阶Fourier逆变换为时域上的一组LFM信号，且这组LFM信号具有相同的调频斜率，不同的中心频率，中心频率间隔为2π/T。若选取这样的一组LFM信号作为子载波，则各子载波的频率为

且有

从式(8)中可以证明，通过式(6)选取出来的各LFM子载波之间的确是正交的。因此，通信系统发射端的载波信号可以写为

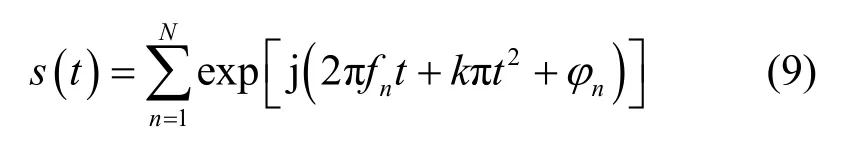
不 妨 令 k=-cotα ，fn=n/T ， φn=φ0+φn’， 且φ0=-(n2πsin2αcotα)/T，其中，φ0为信号的初始相位，φn’为调制的信息相位，T为发射信号的符号长度Tsymbol。于是实现了在发射端将信息相位调制到正交的 LFM 载波的过程。当正交的载波经过理想信道，在接收端对其进行分数阶 Fourier变换即可解调出相位信息。用式(10)表示解调过程为

然而在实际中，积分时间长度为符号长度Tsymbol，所以式(10)可以进一步写为

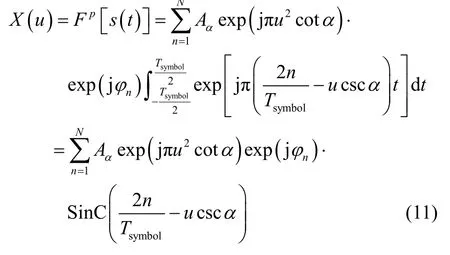
显然由式(11)可得，在接收端经过相位补偿之后，接收信号在分数阶域上呈现出一系列 SinC函数相互叠加的形式，且每个 SinC函数的峰值点均位于其他SinC函数的零点处，如图2所示，这一点也说明了所有的LFM载波是相互正交的，不会产生子信道之间的干扰，因而每个载波可独立的解调出发射端调制的相位信息。至此，证明了存在这样一组正交的LFM信号载波，其频带相互重叠，利用分数阶Fourier变换可以独立的解调出每个载波的相位信息，具有较高的频带利用率和通信速率。

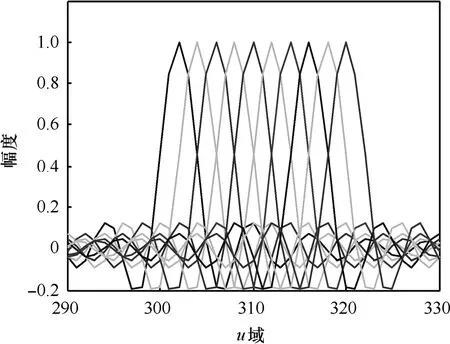
图2 一帧FRFT-OFDM数据中分数阶域正交LFM子载波

整体通信体制如图3所示，首先将信源所产生的信息比特流进行QDPSK星座映射得到相位数据流，然后将其做串并转换分成L帧的N点相位，将这N点相位补齐成数据帧长度M并做M点逆分数阶Fourier变换，相当于将N点相位调制到对应N个正交的 LFM 子载波中，最终再进行并串转换将这L帧信号合并成发射数据信号。为应对信道的多途时延扩展，在每帧信号之间添加保护间隔(GI)。接收端接收换能器将信道中传播的声信号转换成电信号，经前置调理电路滤波放大后采样处理，首先根据接收信号中的同步信号进行时间定位和多普勒系数的估计，然后将数据流恢复成包含保护间隔的数据帧。去除保护间隔后对接收信号做分数阶Fourier变换，通过多普勒效应补偿和差分相位解调即可在u域上获得调制的相位信息。根据解调出来的相位，经星座反映射恢复成二进制比特数据流，至此基于分数阶 Fourier变换的正交多载波水声通信系统完成。

4 多普勒效应补偿分析

海水介质为有损非均匀介质，由于海水的非均匀性，且海水中的洋流和暗涌及收发平台的相对运动，均可造成接收信号产生多普勒效应。多普勒效应对信号的影响是载波频率的偏移和时间宽度的压扩[19]，其频偏Δf可以表示为

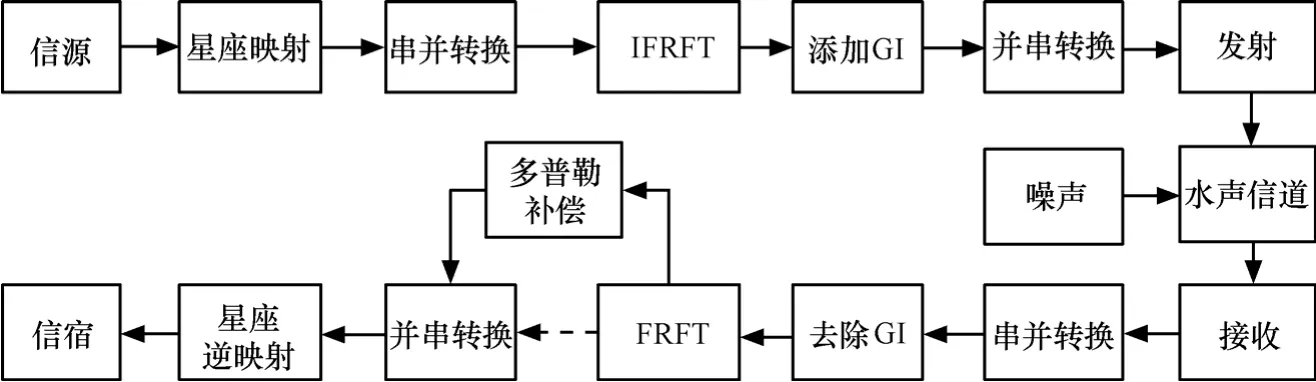
图3 FRFT-OFDM水声通信系统设计

其中，fc为载波频率，c为声速，v为收发平台相对运动速度，θ为运动速度与信号传输方向的夹角。因此可以得知传统OFDM系统中，不同子载波的多普勒频偏是不一致的，从而子载波正交性遭到严重的破坏，产生严重的子载波间干扰，使得通信系统的性能急剧下降。

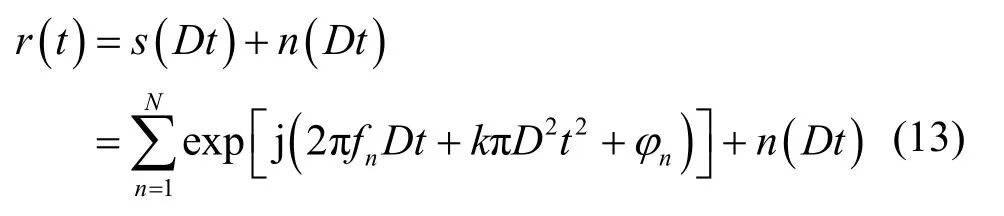
其中，D为多普勒效应对信号的压缩系数，D=1+δ，δ为多普勒系数，δ=v/c。因此，从式(13)中可知，多普勒效应对 LFM 信号的影响，不仅是使其中心频率的移动，还有调频斜率的改变。但是当D≈1时，可以认为接收的 LFM 信号相对于发射信号仅有一小段频移[13]。在水声通信中，若通信平台以 20节航速作相向运动，则可以算得信号的多普勒压缩系数约为 D=0.994，近似等于 1，因此，多普勒效应对 LFM 信号的影响可以认为是仅有频率的移动而没有调频斜率的变化。因而在对受多普勒效应影响的接收信号作分数阶 Fourier变换时，可以依旧采用原信号的变换阶次进行匹配而无需做出调整。由式(5)可得，当多普勒效应的影响不足以使得分数阶Fourier变换的阶次p发生变化时，即时频面旋转角度不会发生变化，则α’=α，此时式(5)分数阶Fourier变换尺度变换特性可以化简为

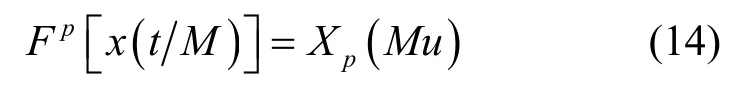
令M=D-1，结合式(14)和式(11)，则基于LFM载波的正交多载波系统接收信号受多普勒效应影响后的分数阶Fourier变换为

式(15)说明通信系统各 LFM 子载波依旧是正交的，不会产生ICI，只是在变换域u域上进行了尺度的变换，且载波位置发生了变化，由nsinα/Tsymbol移动到 Dnsinα/Tsymbol。式中第 2 项说明每个子载波产生了附加相移，且相移大小与子载波位置有关。因此，在实际系统中只需采用 QDPSK调制体制，并估计出接收信号的多普勒效应的时间压扩系数D，根据D修正子载波在u域中偏移位置，就可以消除子载波的附加相移从而解调出发送端调制的信息相位。

因此，本系统具有较强的抗多普勒效应的能力，只需在接收信号变换域做简单的载波位置修正，无需其他任何复杂的计算，大大简化了系统的复杂程度，从而有利于将本系统应用于实际当中。

5 仿真研究与湖试实验结果

为验证通信系统的可靠性及有效性，本文采用计算机仿真验证。通信系统数据帧结构如图 4所示。每帧数据由同步码、间隔码和信息码构成。同步码选择大时延带宽积的LFM信号，其作用有2点：第一，为本帧数据开始提供定时信息；第二，和下一帧的同步码联合估计出接收信号的时间宽度，用以测出信号的多普勒压扩系数，从而补偿多普勒效应。

信息码选择载波带宽为1kHz，时宽为0.01s，频带覆盖范围从 3～9kHz，中心频率间隔为 300Hz的 18个正交的 LFM 子载波，每个子载波采用QDPSK调制，格雷码映射，因而理论通信速率可达3.6kbit/s。

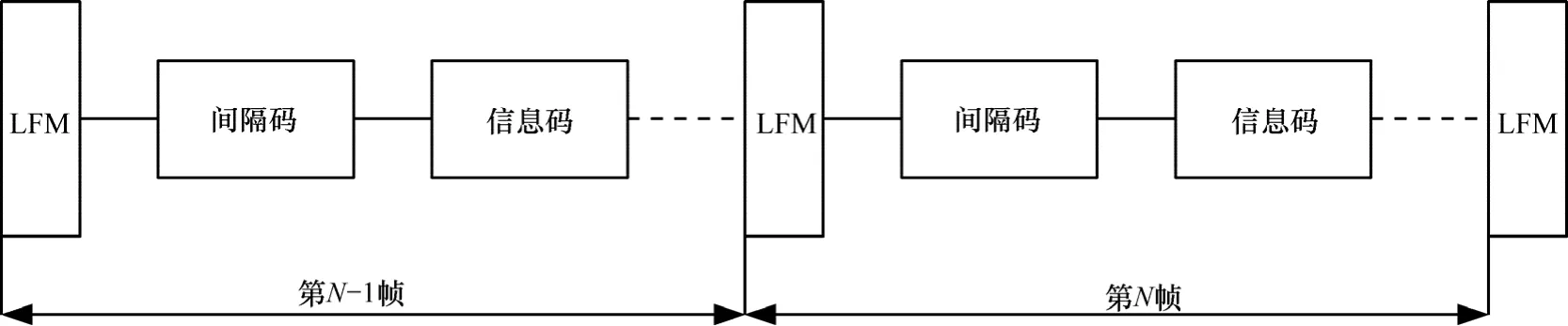
图4 数据帧结构

根据实测水文数据及换能器的布放(发射换能器深度20m，接收换能器30m，距离3 000m)，采用某声纳预报软件，计算出信道函数的频率响应如图5所示，可见信道在通信频带内有4个深度衰落的零点。图6给出的是当信噪比为15dB时，2种通信系统的子载波误码率比较，其中图 6(a)给出的是FFT-OFDM 通信系统子载波的误码率，系统数据帧长度为0.017s，采样率为60kHz，选用61～160号频点来传输数据，可见其2～5号、56号、73～76号、89～92号载波对应于信道4个零点，均出现较大的误码，尤其是第 5号载波，出现了完全的误码，因此深度频率选择性衰弱信道极大地恶化了 FFT-OFDM系统的性能；图6(b)给出的是FRFT-OFDM系统子载波误码性能，各LFM子载波均较好地克服了信道的频率选择性衰落效应。本文对多普勒效应的补偿也做了相应的仿真，图 7(a)给出的是在 SNR=15dB的条件下，当收发平台相对运动速度为 15m/s(航速30节)，未补偿多普勒效应的星座图，可见多普勒效应及分数阶Fourier变换对各子载波的不同的附加相移使得解码相位产生了严重的相位旋转，图 7(b)给出的是采用 QDPSK和载波位置偏移修正补偿多普勒效应后的星座图，纠正了相位旋转，可见本文所提的通信方案能够采用简单的方法良好地应对较大多普勒条件下的移动通信环境。

图8(a)给出的是相同条件下文中所提基于LFM载波的 FRFT-OFDM 调制方法与基于正弦载波的FFT-OFDM调制方式的误码率性能比较。采用蒙特卡洛法仿真，在不加信道编码的情况下，FRFT-OFDM的误码性能较传统的FFT-OFDM有较大地提升，这意味着FRFT-OFDM更加适应以空时频变、频率选择性衰弱为特点的水声信道。并且从图中可以得出，在中低信噪比条件下，FRFT-OFDM可以取得更好的效果，因而相较于FFT-OFDM更适合于在较远的通信距离和更加复杂的水文条件环境下工作，究其原因是因为以宽带信号为载波的信号处理增益要远大于窄带信号，这就使得 FRFTOFDM具有良好的稳健性。图8(b)给出了采用在帧与帧之间加入保护间隔(GI)的方法可以有效地减少符号间干扰，减少误码的出现。

图5 信道函数的频率响应

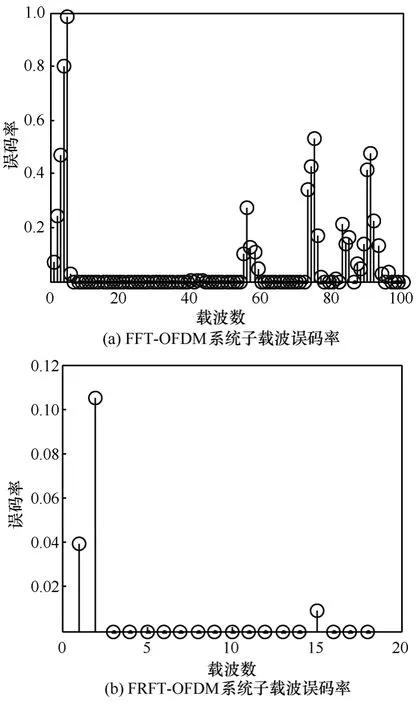
图6 SNR=15dB时子载波误码性能对比

图7 SNR=15dB时相对运动速度15m/s解码星座图

图8 误码性能曲线

为验证该方案的可行性，本课题组与2010年9月在黑龙江省牡丹江市莲花湖进行了湖试实验。莲花湖呈狭长型，水域不够开阔，平均水深约40m左右，湖底原为村庄，后因建坝发电而将村庄淹没，因而湖底地形十分复杂，造成实验湖区信道条件比较恶劣。

实验分为定点通信实验与移动通信实验2个部分。定点通信中发射节点(信源)和接收节点(信宿)分别位于2条自由漂泊的船上，发射换能器布放深度 5m，接收换能器布放深度 10m。两船发动机关闭，在风力与水流的作用下具有缓慢的相对运动。定点通信共在3个距离上实现，用GPS测量当时的通信距离大约在1 000m、2 000m和3 000m。图9中(a)～(c)分别为这3个距离上接收信号解码的星座图和误码率。表1给出的是以上不同通信距离有无保护间隔的误码率对比，数据显示保护间隔在实际情况中的确能够有效减小误码的产生。

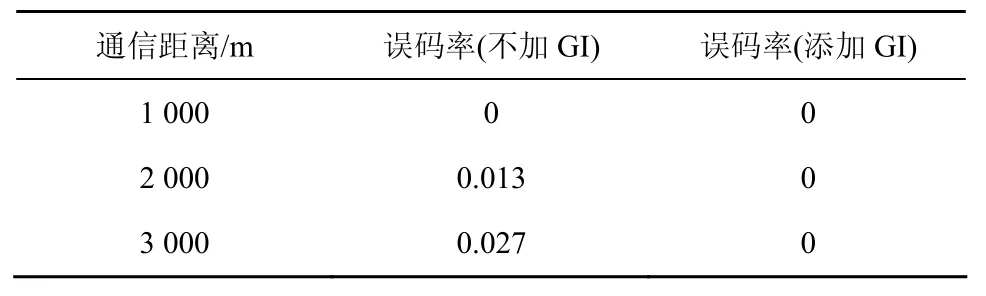
表1 不同通信距离的误码性能

移动通信实验接收平台锚定在锚地，发射平台由距接收平台3 000m处驶向锚地，在距离接收平台1 000m处反向驶离锚地，采用GPS测得相对运动速度为2.7m/s(航速5节)。因为实验所用船只为当地游船，因而无法获得大航速的实验条件(5节是最高航速)。图9(d)给出的是经过多普勒效应补偿后的解码星座图，经过多次移动通信实验均验证本方案提出的分数阶域载波位置修正结合QDPSK调制的方法确实能够有效地补偿通信平台相对运动的多普勒效应，取得零误码的效果。

6 结束语

本文给出了一种以 LFM 信号为载波的基于分数阶 Fourier变换正交多载波水声通信方案，并且对这个方案做出详细的理论公式推导和仿真实验研究，与均采用宽带信号的Pattern编码体制、扩频水声通信等常规通信方法相比，在保证通信质量的前提下大幅提高了水声通信的通信速率，并通过湖试实验验证本方案的可行性。基于分数阶 Fourier变换的正交多载波通信系统相较于传统的 OFDM系统对频率选择性衰落信道更具有适应性，无需采用后续复杂的信道估计算法，且采用宽带信号载波具有更高的处理增益使得本方案更加适用于远距离通信或复杂水文条件下的工作环境。LFM信号受多普勒效应影响后的分数阶 Fourier变换可以近似简单认为是载波位置的移动且附加有相移，使得本方案无需复杂的多普勒效应补偿算法，简化了系统复杂度，可应用于移动平台的通信。因此本方案对于高速、复杂情况的水声通信环境来说具有广阔的应用前景。

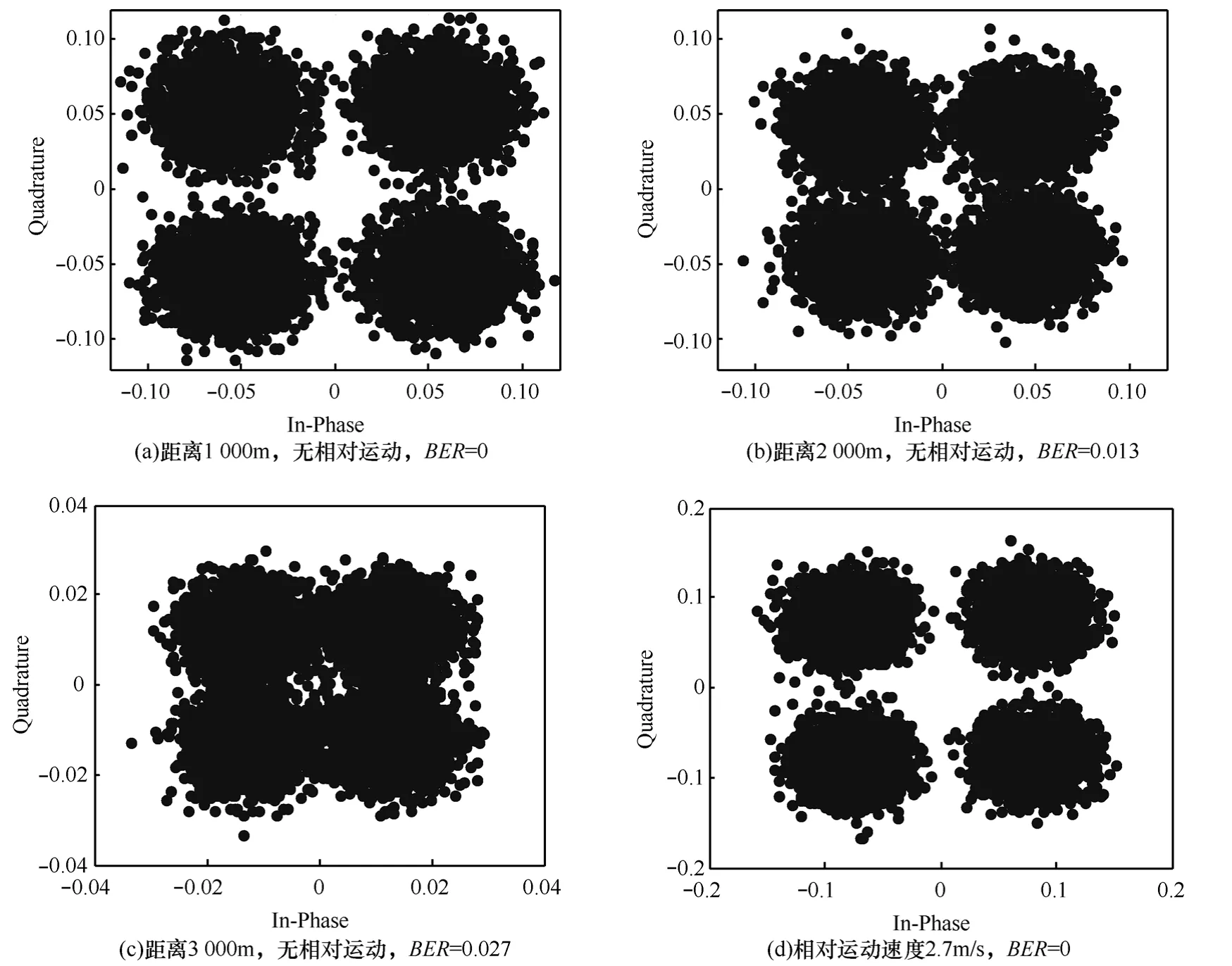
图9 湖试实验解码星座图

[1] 惠俊英. 水下声信道[M]. 北京：国防工业出版社，1992.HUI J Y. Underwater Acoustic Channel[M]. Beijing: National Defense Industry Press, 1992.

[2] 殷敬伟，张晓，赵安邦等. 时间反转镜在水声通信网上行通信中的应用[J]. 哈尔滨工程大学学报，2011，32(1):1-5.YIN J W, ZHANG X, ZHAO A B, et al. The application of a virtual time reversal mirror to upstream communication of underwater acoustic networks[J]. Journal of Harbin Engineering University, 2011,32(1):1-5.

[3] 殷敬伟. 水声通信原理及信号处理技术[M]. 北京：国防工业出版社, 2011 YIN J W. The Theory and Signal Processing Technology of Underwater Acoustic Communication[M]. Beijing: National Defense Industry Press, 2011.

[4] SAVALONAS M A, CHOUNTASIS S. Noise-resistant watermarking in the fractional Fourier domain utilizing moment-based image representation[J]. Signal Processing, 2010, 90(8): 2521-2528.

[5] MARTORELLA M. Novel approach for ISAR image cross-range scaling[J]. IEEE Aerospace and Electronic Systems, 2008, 44(1): 281-294.

[6] BARSHAN B, AYRULU B. Fractional Fourier transform preprocessing for neural networks and its application to object recognition[J].Neural Networks, 2002, 15(1): 131-140.

[7] 陈恩庆, 陶然, 张卫强等. 一种基于分数阶傅里叶变换的OFDM系统及其均衡算法[J].电子学报, 2007, 35(3): 409-414.CHEN E Q, TAO R, ZHANG W Q, et al. The OFDM system and equalization algorithm based on the fractional Fourier transform[J].Acta Electronic Sinica, 2007, 35(3): 409-414.

[8] 陈恩庆, 陶然, 张卫强等. 分数阶傅立叶变换OFDM系统自适应均衡算法[J]. 电子学报, 35(9): 1728-1733.CHEN E Q, TAO R, ZHANG W Q, et al. The adaptive equalization algorithm for OFDM system based on the fractional Fourier trans-form[J]. Acta Electronic Sinica, 2007, 35(9): 1728-1733.

[9] TAEHYUK K, RONALD A. Iltis. Iterative carrier frequency offset and channel estimation for underwater acoustic OFDM systems[J]. IEEE Journal on Selected Areas in Communications, 2008, 26(9): 1650-1661.

[10] GREERT L, PAUL A W. Multiband OFDM for covert acoustic communications[J]. IEEE Journal on Selected Areas in Communications,2008, 26(9):1662-1673.

[11] RUGINI L, BANELLI P, LEUS G. Simple equalization of time-varying channels for OFDM[J]. IEEE Communication. Letters,2005, 9(7):619-621.

[12] 陶然, 邓兵, 王越. 分数阶傅里叶变换的原理与应用[M]. 北京：清华大学出版社，2009.TAO R, DENG B, WANG Y. Fractional Fourier Transform and Its Applications[M]. Beijing: Tsinghua University Press, 2009.

[13] 田坦, 刘国枝, 孙大军. 声呐技术[M]. 哈尔滨：哈尔滨工程大学出版社, 2000.TIAN T, LIU G Z, SUN D J. Techniques of Sonar[M]. Harbin: Harbin Engineering University Press, 2000.

[14] 殷敬伟, 惠俊英, 蔡平等. 分数阶Fourier变换在深海远程水声通信中的应用[J]. 电子学报，2007, 35(8): 1499-1504.YIN J W, HUI J Y, CAI P, et al. Application of fractional Fourier transform in long range deep-water acoustic communication[J]. Acta Electronic Sinica, 2007, 35(8): 1499-1504.

[15] 陶然，邓兵，王越. 分数阶 Fourier变换在信号处理领域的研究进展[J]. 中国科学（E辑），2006, 36(2): 113-136.TAO R, DENG B, WANG Y. Research advance in fractional Fourier transform in the signal processing region[J]. Science in China Ser E Information Science, 2006, 36(2): 113-136.

[16] OZAKTAS H M, ARIKAN O, KUTAY A A, et al. Digital computation of the Fourier transform[A]. IEEE Tran Signal Processing[C].1996. 2141-2150.

[17] CANDAN C, KUTAY M A, OZAKTAS H M. The discrete fractional Fourier transform[A]. IEEE Tran Signal Processing[C]. 2000. 1335-1348.

[18] PEI S C, DING J J. Closed-form discrete fractional and affine Fourier transform[A]. IEEE Tran Signal Processing[C]. 2000. 1338-1353.

[19] 李红娟，孙超. 加速度下的水声通信多普勒频移补偿方法[J]. 西北工业大学学报，2007, 25(2): 181-185.LI H J, SUN C. Effective Doppler compensation for underwater acoustic communication under relative acceleration[J]. Journal of Northwest Polytechnical University, 2007, 25(2): 181-185.