基于多符号分组的CPM软输出非相干检测算法

杨友福，刘建伟，张其善，修春娣

（北京航空航天大学 电子信息工程学院，北京 100191）

1 引言

卫星和移动通信系统具有带宽、功率受限以及信道非线性等属性[1]，系统设计需要选择具备较高频谱和功率效率的调制方式。CPM技术[2]因为相位连续、功率谱旁瓣小的特性十分适合此类带宽受限系统。同时，CPM信号的恒包络特性允许功率放大器工作在饱和状态，能够很好地适应非线性信道，从而获得较高的功率效率。随着级联编码和迭代检测技术的发展，纠错编码技术与 CPM 的串行级联方案被提出[3]， CPM能够与卷积码、Turbo、LDPC等多种信道编码技术级联构成不同SCCPM方案，在接收端采用迭代检测技术，能同时获得很高的带宽和功率效率。由于CPM可以被分解为CPE（连续相位编码器）和 MM（无记忆调制器）级联[4]，因此，针对 CPM 的最优接收机通常是由匹配滤波网络和基于网格的译码器相级联构成相干接收机，这需要检测器能够获得良好的载波相位、信号时序以及信道状态等信息。然而，SCCPM 系统一般工作在较低的信噪比条件下，这对上述参数估计十分不利，况且在一些跳频、信道快变的窄带系统中要想准确估计这些参数需要复杂的电路和算法，代价十分昂贵。CPM信号的非相干检测技术可以在性能和实现复杂度方面获得较好的折中。文献[5,6]研究了单符号差分检测技术，实现复杂度低但性能损失较大；文献[7,8]研究了基于多个符号的差分检测技术，以一定的复杂度增加获得了性能改善；文献[9]给出了一种基于最大似然算法的非相干检测技术，在检测复杂度和性能方面获得了较好的均衡。

本文以串行级联SCCPM方案为背景，提出了一种基于多符号分组的 CPM 软输出非相干检测算法，对CPM 信号检测时，首先以连续多个符号作为观测窗计算出传输信号的条件转移概率，然后以此计算出每个比特对应的外信息值，输出给外解码器。该算法不需要信道状态信息，无需在接收端设置额外的估计电路，从而简化了接收机设计，同时，由于 CPM 信号的检测过程不涉及到递归运算，比文献[10～13]中给出的非相干检测算法具有更低的复杂度。仿真表明，提出算法的性能随观测符号长度的增加而提高，以调制阶数分别为2、4的SCCPM方案为例，观测符号长度N=4时比单符号非相干检测具有约6dB的性能增益，况且，对于脉冲类型、关联长度等不同参数的 CPM 信号，提出的算法体现了很好的稳定性。

2 系统模型

串行级联编码CPM方案如图1所示，二进制信息序列 u通过外编码器 Co后输出编码比特序列v，外编码器码率 Ro= k / n，k为输入的信息比特数，n为输出的码字比特数，编码比特序列v通过交织器π和符号映射器b-s后生成符号序列 w = ｛ wi｝,比特到符号映射可以采用自然或者格雷映射方式，且有 wi∈｛±1 , ±3 ,… ,± ( M -1)｝ ，M为调制阶数，取 2的n次幂，符号序列w输入到CPM调制器产生调制信号 xn( t, w)，此处CPM调制器可以看作CPE和MM的串行级联，CPE作为SCCPM方案的内编码器。CPM信号 xn( t, w) 依次通过AWGN(加性高斯白噪声)信道、接收端匹配滤波网络及迭代译码器后最终输出解码比特序列uˆ，图1中rn( t)表示接收的信道信号， rn为匹配滤波后得到的充分统计量，迭代译码器各个单元同发送端相对应，不再赘述。

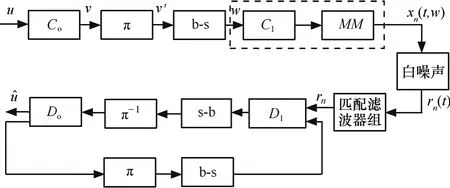
图1 串行级联编码CPM方案

CPM发送信号 xn( t, w)取自集合

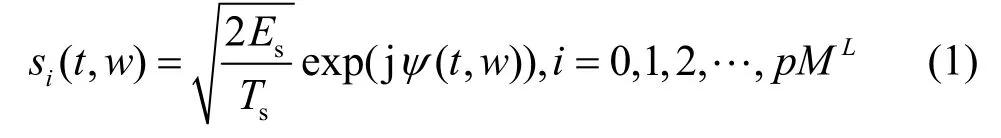
其中，sE为符号能量，sT为符号持续周期，时刻的相位轨迹为其中，为累积相位，设初始值00θ=。为相关相位，调制指数 /h q p= 为有理数（ ,q p为互质数），L为频率脉冲相关长度， f(t) 为相位响应，满足CPE网格状态可以用表示，CPM信号由状态nσ和当前输入符号nw确定。

3 符号分组CPM非相干检测算法

发送信号 xn( t, w)通过AWGN信道后，接收信号复包络可表示为假设接收端可以获得良好的信号时序同步，nn( t)为复高斯随机过程，具有单边功率谱N0（W/Hz），φn为信道引入的相位噪声，在所关注的符号分组内为未知常量φn=φ，服从[-π, π)区间的均匀分布。在图1中，模块 DI执行CPM信号的非相干检测，其前端模块首先对 rn( t)进行匹配滤波，共有2 ML个实数滤波器，并以符号间隔时间采样后输出充分统计量：

其中， xn为信号成分， nn为高斯噪声成分，为了实现CPM 信号的非相干检测，检测器 DI以N个连续符号时间长度为一个观测窗口，如果定义 Tn= [ (n - N1) T,(n + N2) T]为观测窗，那么有 N = N1+ N2+1，Tn内的接收统计量可以表示为因为相关长度为L，所以与 Tn相关联的调制符号序列可表示为AWGN信道条件下，条件概率密度[9]：

对式(3)展开，并去除对于所有可能iw的公共项得到

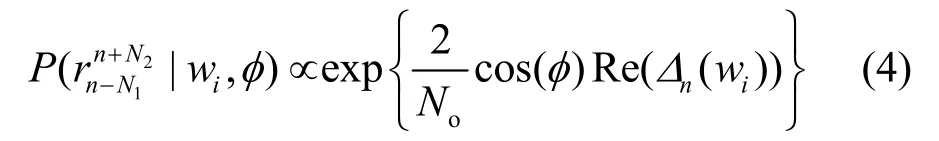
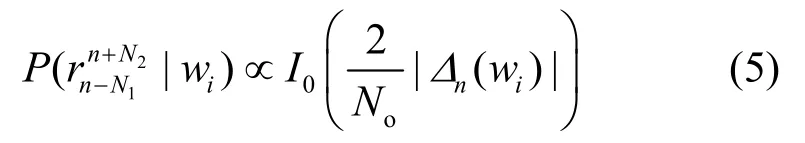
其中， I0(·)为第一类零阶修正贝塞尔函数， Δn( wi)可以通过递归方式求解：

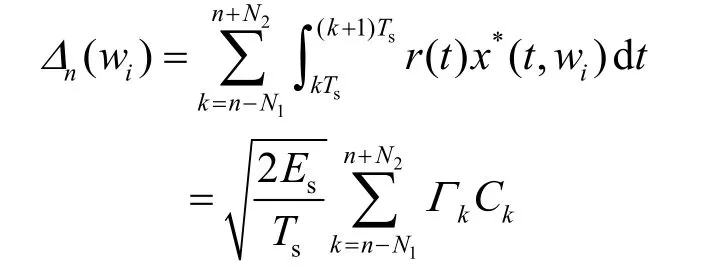
这里

需要注意的是，Δn( wi)的值并不依赖于区间开始t = (n - N1) T 时刻的累积相位状态θn-N1，因此非相干检测并不需要知道θn-N1的确切值，可以令θn-N1= 0 。

由于图1中外编码器和CPM调制器通过比特交织级联，在迭代译码阶段软输出译码器 DI和 Do相互交换比特外信息，因此 CPM非相干检测器需要输出基于比特的外信息。与符号序列 wi相关联的比特序列可表示为 b ( wi) = { b0, b1, … ,b(NlogM-1)}，bk(wi)为b( wi) 的第k个比特，那么非相干检测器输出比特 bk(wi) 的外信息为

由于采用基于比特交织器，这里

其中，λ ( bj( wi))为比特 bj( wi) 的先验LLR值，由外译码器 Do反馈的软信息经过交织得到。将式（5）带入到式（7），并采用操作符则非相干检测器 DI输出的比特外信息为

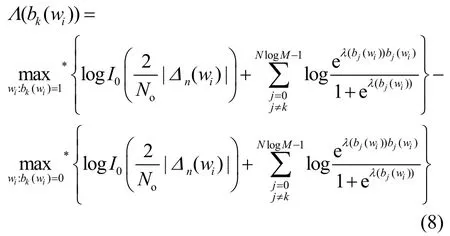
Λ(bk( wi))经过解交织器 π-1后输入到外码译码器 Do， Do通过软译码算法（如BCJR类算法）产生比特外信息，外信息经由交织器π和b-s构成的反馈路径输入到内译码器 DI，从而完成一次迭代译码，当满足预先设定的迭代停止准则时译码停止，由 Do输出的比特似然信息进行判决，输出译码比特序列，完成解码操作。

为了减小计算复杂度，函数 I0(·)可以采用分段函数进行近似，项 Δn( wi)中的Γk分量可以通过Walsh基函数扩展方式进行近似，此处 rkj、 skj分别是接收信号 rk( t)和参考信号 si( t, w)在选定Walsh函数空间的坐标值，具体计算方法可以参见文献[14]。J是 Walsh空间维数，对大多数CPM信号， J = 4 时接收机性能可以接近最优。由于Walsh函数取值为+1，-1，接收机前端无需进行原有的匹配相关运算，只需对接收信号进行积分并以速率J进行采样，简化的接收机结构如图2所示。

图2 简化的CPM非相干检测器

相比于最佳相干接收，提出的 CPM 非相干检测算法以及接收机方案有效降低了接收机的硬件实现复杂度：非相干检测无需载波相位信息，省去了相应参数估计单元以及计算量；其次，接收机前端基于Walsh函数扩展，避免了采用大量匹配滤波器组，这也同样降低了硬件复杂度；另外，与基于BCJR算法的检测方式[11]相比，基于符号分组的软输出非相干检测算法无需计算前向、后向递归量，也可以有效减小计算量。

4 仿真研究

利用计算机仿真检验本文提出的非相干检测算法性能，SCCPM方案如图1所示，外码采用非递归（7,5）卷积码，码率为 1/2，编码器和 CPM调制器间采用随机比特交织器，交织长度为1024bit，CPM调制参数根据不同的仿真方案选择，比特到符号选择自然映射，信道为AWGN信道。为了降低接收机计算复杂度并保证一定的系统误码性能，匹配滤波器前端采用Walsh正交基扩展方式，对于2CPM（阶数为2的CPM调制方式）采用4维基函数，对于4CPM采用8维基函数，CPM检测分别采用相干和非相干2种方式，对于非相干检测符号分组长度分别取1、2、4这3种，卷积码采用 MAP算法，迭代译码次数设定为 6。图 3～图6给出了不同CPM调制参数情况下SCCPM系统的误码率性能，为了便于表述以1REC2CPM（频率脉冲为矩形，关联长度为L=1，调制阶数M=2，类似地 1RC表示频率脉冲为升余弦）表示一种SCCPM方案。图3为调制指数h=1/2、1REC2CPM系统性能，CPM 采用相干接收的迭代检测性能最佳，无误码传输的最小信噪比约为3dB，采用N=1单符号非相干迭代检测性能最差，无误码传输的最小信噪比约为12.5dB，二者性能差距为9.5dB，当N=2时无误码传输的信噪比为10.5dB，而N=4时为6.4dB，可见，增加观测符号长度可以提高非相干迭代检测性能，N=4时比单符号非相干检测有6.1dB增益，比N=2时有4.1dB增益，与相干检测情况相差3.4dB。图4为h=1/2、1RC2CPM系统仿真结果，频率脉冲为升余弦形式，性能与矩形脉冲情况相近。图5为h=2/3、2RC2CPM系统性能，可见，部分响应频率脉冲形式下非相干迭代检测性能略差于全响应CPM调制方案，检测性能依然随着观测符号长度的增加而提高。图 6为 h=1/4、1RC4CPM和1REC4CPM 2种系统仿真结果，与2CPM调制具有同样特性，N=4符号非相干检测优于单符号非相干方法约 6dB，与相干检测相距约2.5dB。综上可知，提出的多符号CPM非相干检测算法能够较好地应用于具备高谱效率、高功率效率的SCCPM系统中，给定外编码器、交织器、迭代次数等系统参数时， 对于CPM调制指数、阶数、频谱脉冲以及关联长度等参数的不同取值，提出的非相干检测算法呈现出较好稳定性，等效最小欧式距离[15]随着观测符号长度的增加而增加，检测性能也随之改善。

图3 1REC2CPM，h=1/2系统性能

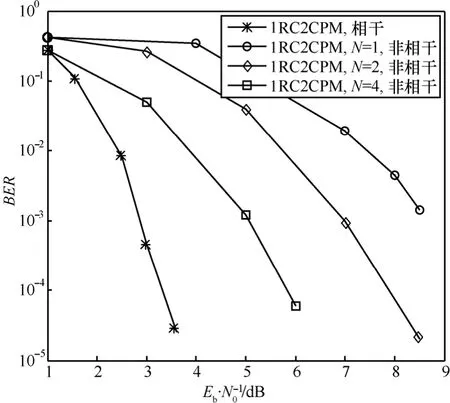
图4 1RC2CPM，h=1/2系统性能

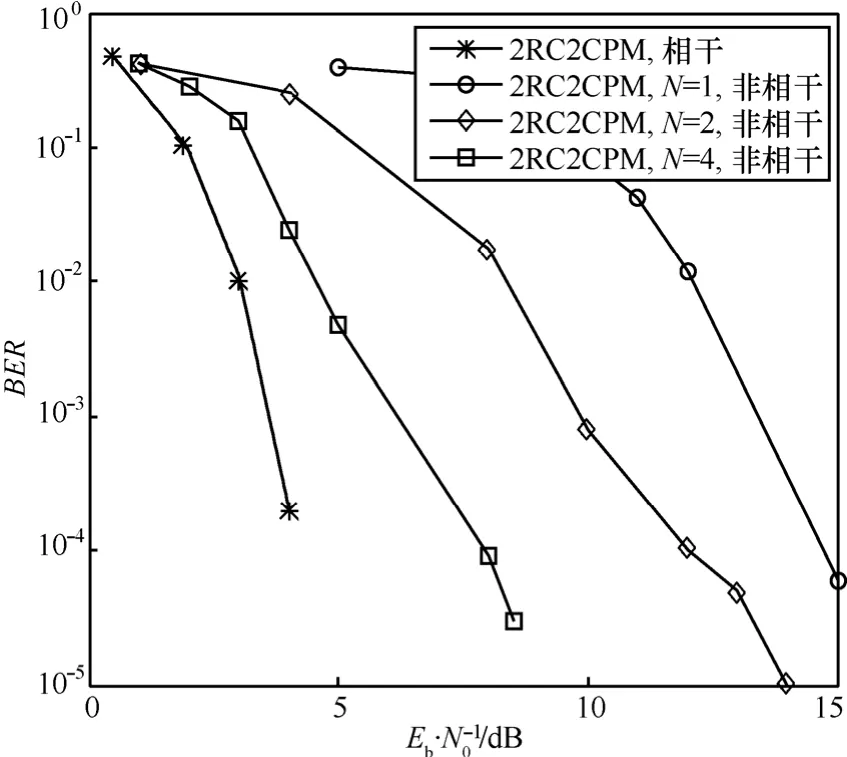
图5 2RC2CPM，h=2/3系统性能

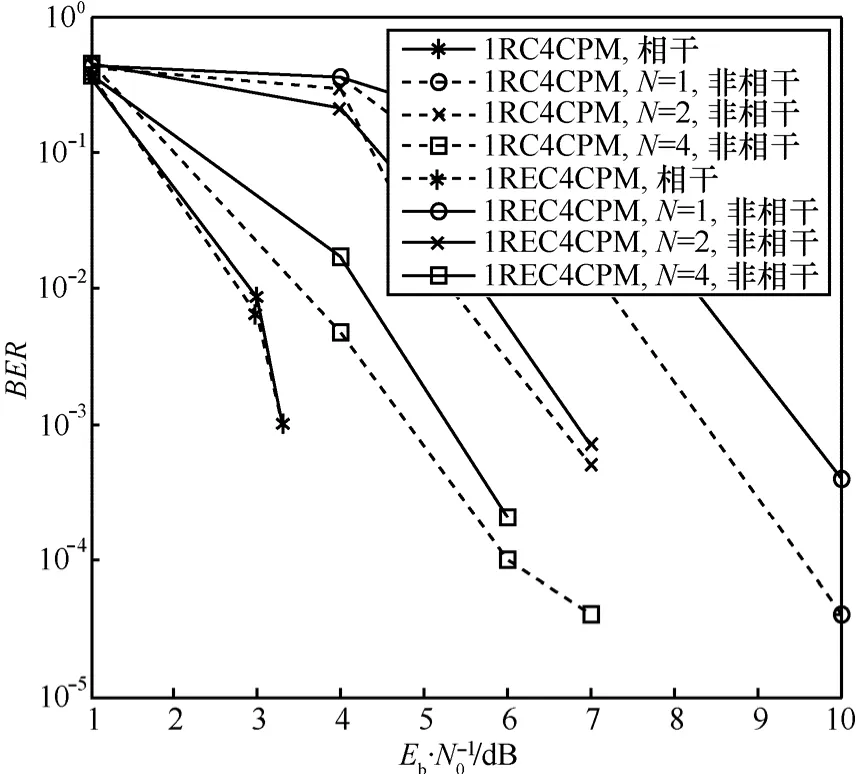
图6 4CPM，h=1/4系统性能

5 结束语

CPM 调制固有的相位连续和恒定包络特性使其非常适用于带宽、功率受限以及信道非线性的卫星通信系统，CPM 与信道编码技术级联构成的SCCPM 系统可以获得很高的功率效率。针对SCCPM 系统工作信噪比低和信道参数估计复杂的问题，提出了一种符号分组软输出 CPM 非相干检测算法，算法不需要信道状态信息，无需在接收端设置额外的信道估计电路，从而节省大量计算资源。提出的SCCPM接收机与最优相干接收结构类似，接收前端基于Walsh基函数进行空间映射以简化匹配滤波计算量，CPM解调采用提出的符号分组软输出非相干检测算法，信道译码则采用基于MAP的通用SISO算法，迭代译码的性能随着所设定观测符号长度的增加而提高，对于2阶、4阶SCCPM级联方案，N=4符号较单符号非相干检测具有约6dB性能增益，距离相干检测有3.4dB和2.5dB差距，因此，提出的多符号分组 CPM 非相干检测算法是以一定的性能损失换取接收机复杂度的简化，实际系统设计应该从性能需求和实现复杂度2个方面进行考虑。

[1] TIMOTHY P, CHARLES B, JEREMY A, et al. Satellite Communications[M]. 2nd Edition, John Wiley & Sons, 2003.

[2] RYDBECK T A N, SUNDBERG C E. Continuous phase modulation(CPM), part I and part II [J]. IEEE Trans Commun, 1981, 29(3):196-225.

[3] MOQVIST P, AULIN T. Serially concatenated continuous phase modulation with iterative decoding[J]. IEEE Trans Commun, 2001,49(11): 1901-1915.

[4] RIMOLDI B. A decomposition approach to CPM[J]. IEEE Trans Inform Theory, 1988,34(3):260-270.

[5] 孙锦华,李建东,金力军.连续相位调制的非相干减少状态差分序列检测算法[J].电子与信息学报,2005,27（8):1338-1341.SUN J H, LI J D, JIN L J. Noncoherent reduced state differential sequence detection of continuous phase modulation[J]. Journal of Electronics and Information Technology, 2005, 27(8): 1338-1341.

[6] ANDERSON J B, AULIN T, SUNDBERG C E. Digital Phase Modulation[M]. New York: Plenum, 1986.

[7] MAKRAKIS D, FEHER K. Multiple differential detection of continuous phase modulation signals[J]. IEEE Trans Veh Technol, 1993,42(1): 186-196.

[8] 乔植, 周春晖, 肖立民. 基于多符号差分相关的 CPM 非相干解调算法[J]. 清华大学学报(自然科学版),2007,47(4):507-510.QIAO Z, ZHOU C H, XIAO L M. Non-coherent demodulation of continuous phase modulation signals based on multi-svmbol differential correlation[J]. Tsinghua Univ(Sci and Tech), 2007,47(4):507-510.

[9] DIVSALAR D, SIMON M K. Maximum-likelihood block detection of noncoherent continuous phase modulation[J]. IEEE Trans Commun,1993,41(1):90-98.

[10] COLAVOLPE G, RAHELI R. Noncoherent sequence detection of continuous phase modulations[J]. IEEE Transactions on Communications,1999,47(9):1303-1307.

[11] COLAVOLPE G , FERRARI G , RAHELI R. Noncoherent iterative(turbo)decoding[J]. IEEE Trans Commun, 2000, 48(9):1488-1498.

[12] HOWLADER, MOSTOFA K, LUO X L. Noncoherent iterative demodulation and decoding of serially concatenated coded[A]. MS GLOBECOM'04-IEEE Global Telecommunications Conference[C].Dallas, TX United States, 2004.11-29.

[13] LI B, BAI B M, HUANG M Y. A robust noncoherent iterative detection algorithm for serially concatenated CPM[A]. ISTC 2010(2010 6th International Symposium on Turbo Codes & Iterative Information Processing)[C]. Brest France,2010.9-6.

[14] WEIYI T, SHWEDYK E. A quasi-optimum receiver for continuous phase modulation[J]. IEEE Trans on Comm, 2000,48(7):1087-1090.

[15] HO-KYOUNG L, WEBER C L. Multiple-symbol trellis-coded modulation applied to noncoherent continuous-phase frequency shift keying[J]. IEEE Transactions on Information Theory, 1997, 43(2):454-468.