乒乓球战术行为博弈分析的理论体系建构
刘文明,唐建军
(1.浙江大学 教育学院体育学系,浙江 杭州310028;2.北京体育大学,北京100084)
乒乓球运动竞赛必然存在某种意识程度上的“交叉效应”,即一方运动员的行为势必会影响对手的策略选择与比赛结果,这种双方队员对交叉效应的认识,以及双方据此认识而采取的战术行动,构成了乒乓球运动竞赛取胜的核心。若三思而后行——明白对手的目标和偏好,以及行动的约束和限制,并根据自己的标准以一种谋略方式选择行动以期得到最好结果——则可称为在理性地行动[1]博弈论为乒乓球战术行为分析增加了一个维度,即与其他决策者的互动。博弈论是关于互动情形下理性行为的科学,不能说博弈论对乒乓球战术进行分析就可以教给我们对抗的秘诀,或确保永不失败[2]因为绝大多数现实乒乓球比赛情形包含了大量的特异性反应和机会元素,但是博弈论可以提供一些思考策略互动问题的一般性原理,可以告诉我们在谋划一个成功策略之前,必须把这些博弈思想和一些具体的计算方法补充到现在所处的场合中,这时博弈论的一般性原理能够为运动员、教练员提供了一个参照点,可以更快、更自信地归纳和总结出具体乒乓球战术博弈特征,在行动中增大成功概率。
1 乒乓球战术行为博弈理论的概念
“博弈”是社会生活中存在的形形色色的需要依靠策略战胜对手的,具有竞争性和对抗性的现象。博弈竞争就是社会实践中有规则可循的、采用计谋的、富有理性的、期望得到理想或满意结果的竞争。体育博弈,是在一定的竞争规则的限定下进行,最具理想意义的竞争。随着体育运动实践的发展,其中充满了各种冲突、对抗与竞争表现出鲜明的博弈特征,促进了体育博弈理论的形成。“体育博弈论”是关于体育竞争的理论体系,是研究体育竞争中如何战胜对手,提高胜算,获取优胜的理论(李益群、谢亚龙)[3]。首先,乒乓球运动实践是一种体育博弈现象,具有强烈的竞争性、对抗性和战术行为策略性;其次,乒乓球战术行为策略具有显著的互动性、相互依存性的特点,即战术行为的交叉效应;再者,乒乓球战术行为的最终目的就是战胜对手取得比赛的优胜。由此三个方面确定了乒乓球战术行为博弈理论,即是关于乒乓球战术行为合理运用的理论体系,是研究如何在乒乓球竞赛实践中战胜对手,提高胜算,获取比赛优胜的理论。乒乓球战术行为博弈理论是以“博弈论”的基础理论、思想方法去研究和探索乒乓球技战术在竞赛过程中合理运用的微观问题的理论,探讨在乒乓球运动竞赛中如何去战胜对手、提高胜算、获取优胜的科学理论。
根据乒乓球比赛规则和战术行为的交叉效应,乒乓球竞赛战术实施过程可以表示为相互作用的耦合系统,根据战术实施过程的相互制约关系,把对抗中参与人所拥有的战术行为集合为,所实施的战术行动表示为 (战术策略选择及实施如:发球落点)看作是对参与人所发生的作用效应,而参与人所拥有的战术行为集合表示为,对的战术行为的反应行可表示为(战术策略选择及实施如:接发球落点)是参与人对参与人的作用所产生的反作用,并再次作用于参与人,如此反复进行。这样博弈双方之间形成耦合系统关系,如图1所示。
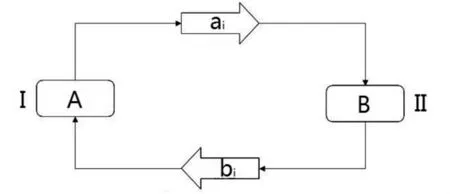
图1 乒乓球竞赛战术行为实施过程耦合关系模型
2 乒乓球战术行为博弈的构成要素
2.1 乒乓球战术行为博弈参与人(players)
乒乓球战术行为的博弈人是指在乒乓球战术行为博弈中独立决策、独立承担博弈结果的个人或者组织,每个参与人的目标都是通过选择行动来最大化自身的效用。只要在一个博弈中统一决策、统一行动、统一承担结果,不管一个组织有多大,哪怕是一个国家,甚至是多个国家组成的联合国,都可以作为博弈中的一个参与人。正在比赛状态时,乒乓球战术行为的发起者为参与竞争的乒乓球运动员,因此乒乓球战术行为的博弈人为直接参与实施技战术的乒乓球运动竞赛的运动员。但教练员往往是运动员战术行为或者是策略的制定者,同时在比赛中也可以实施暂停、手势等等手段间接性参与到乒乓球战术行为的实施过程中,并往往对比赛结果产生巨大影响,所以也是乒乓球战术行为博弈中的重要参与人之一;其次,科研人员对技战术的研究也在逐步地深入到运动实践,给运动员、教练员提过决策支持等,也对乒乓球竞赛战术的使用产生一定的影响。
2.2 乒乓球战术行为博弈的行动(actions or moves)
乒乓球战术博弈中的行动,是参与人在博弈的某个时点的决策变量,在乒乓球运动实践中行动可以指在竞赛过程中某阶段如发球、接发球、第三拍、第四拍和相持过程中的技战术运用,理论上可以从三个层次进行划分:①战术层面有“发球抢攻”,“接发球抢攻”等;②技术层面有控制技术(摆短、劈长)、防守技术(推挡、放高球)及进攻技术(挑打、拉攻)等;③制胜因素层面有力量、旋转、线路、落点、弧线等。
60年代初为中国乒乓球队备战第26届世乒赛形成技战术诊断指标开始,直至第47届世乒赛科研攻关与科技服务的40多年中,确定科研与实践都相对固定的诊断指标。指标体系确定是从实践需要开始,并经过实践筛选,再到实践检验的过程[4]第24、25、26、27届奥运会和其间的4届亚运会及7届世界锦标赛备战训练的检验,证明是可靠的。其中四和五级指标的划分可以看作战术行动在不同博弈分析角度的具体体现,见表1。

表1 战术诊断比赛效果的四级和五级指标
2.3 乒乓球战术行为博弈的信息(information)
在乒乓球战术行为博弈中信息是参与竞争的双方运动员有关此场比赛的博弈知识,有关对手特征和行动的知识。也可以具体表述为双方运动员在特定时间点对于自己和对手特定行动功效的了解。如赛前的比赛技战术分析(录像观察、经验总结)、比赛中已经发生的具体行动知识和对彼此战术风格的了解等都是乒乓球战术博弈的信息。“知己知彼,百战不殆”体现了博弈信息的重要性,现代比赛技战术分析工作已经非常深入,对运动员的技战术分析也相当全面,中国乒乓球队建立了大量的国外乒乓球运动员的战术信息库。并能够以多媒体的形式来展现国外主力队员的技战术信息。
基于比赛视频技术发展起来的多媒体技战术分析,能以视频、动画和图表数据等多种形式清楚有序,生动形象地将对手的技战术特点展示出来,从而有效地帮助教练员和运动员更加细致地观察、分析对手,提高大赛前备战训练的针对性与科学性[5]。

图2 中国国家乒乓球队业务学习多媒体资料
乒乓球战术博弈信息的特点是参与竞争双方的运动员的“共同知识”(common knowledge),这是一个非常重要的概念[6]。共同知识指的是“双方乒乓球运动员知道,双方运动员知道双方运动员知道,双方运动员知道双方运动员知道双方运动员知道…的知识”,在乒乓球战术博弈中,每个参与人的行动集合都是共同知识。比如说参与人知道自己的行动集合,参与人知道参与人的行动集合,参与人知道参与人知道自己的行动集合,参与人知道参与人知道参与人知道自己的行动集合,如此等等。
2.4 乒乓球战术行为博弈的战略(strategies)
乒乓球战术行为博弈的战略指的是参与人(乒乓球运动员)在给定信息的情况下的行动规则,它规定了参与人(乒乓球运动员)在什么时候选择什么行动。因为信息集包含了一个参与人有关其他参与人之前行动的知识,战略告诉该参与人如何对其他参与人的行动做出反应,因而战略是参与人(双方运动员)的“相机行动方案”(contingent action plan)。
乒乓球战术行为博弈的战略根据乒乓球项目具体实施过程可进行两个层面的划分:乒乓球战略构成策略层面可以理解为战术单元、单个战术和若干单个战术构成的战术体系——战术风格。乒乓球战术最基本的战术形式是战术单元,所谓战术单元是指单一技术的战术化,比如目的性、策略性地使用发球而直接得分。而所谓策略,是指在单一技术的使用中,根据对手情况,通过速度、力量、旋转和落点线路的变化来争取得分。战术单元是构成战术的基本“细胞”,两个以上的战术单元构成了单个战术。所谓单个战术就是结合技术的战术化,如反手用推挡压住对手反手大角度获得主动后,伺机侧身正手进攻得分。若干单个战术组合构成一个战术体系[7]
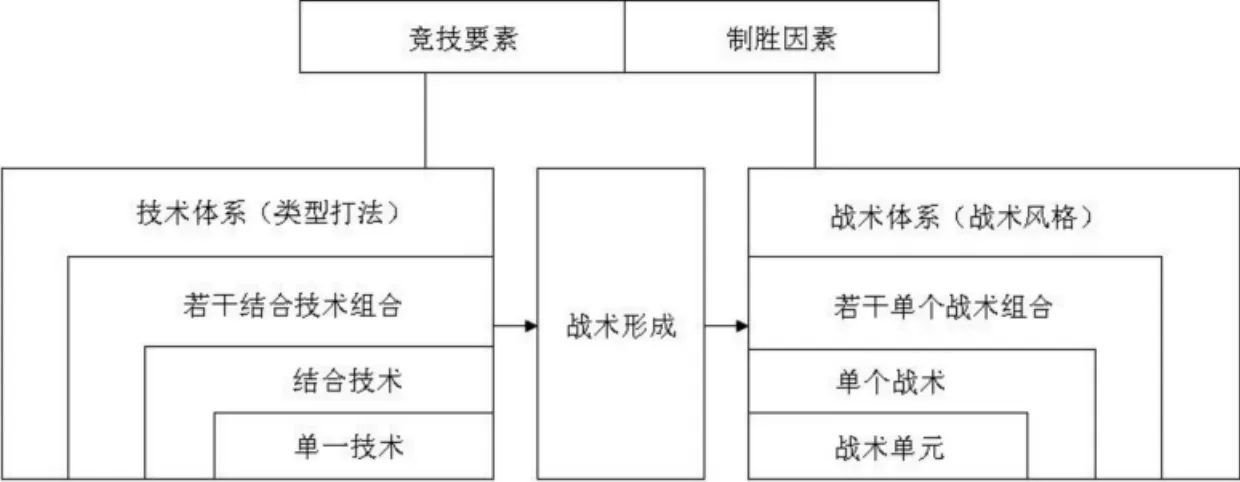
图3 乒乓球技术、战术和战术形成结构与关系模式图
乒乓球战术行为博弈的战术层面主要指战术的数量,包括进攻战术的数量、控制战术的数量和防守战术的数量。战术数量是战术能力在数量上的体现,它是战术质量存在的基础。在比赛中单一战术,会使对手很快适应,在高水平的比赛中是没有质量可言的。在乒乓球的基本战术中进攻打法类型的战术包括:发球抢攻战术;对攻战术;拉攻战术;搓功战术;接发球战术。削攻或削攻结合打法类型的战术包括:发球抢攻战术;削攻(攻削)结合战术;搓、攻、削结合战术;搓攻战术;接发球战术。运动员必须掌握多种战术,才能提高战术的应变能力,争取战术运用的主动[7]。
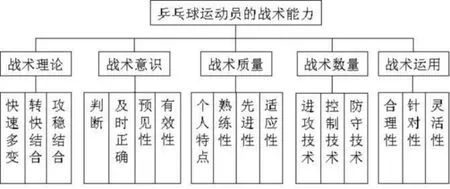
图4 乒乓球运动员战术能力系统构成图
2.5 乒乓球战术行为博弈的得益(payoffs)
支付在乒乓球战术行为博弈中指的是特定战略组合下参与人(双方运动员)的确定效用水平,或是指参与人得到的期望效用水平。对应于乒乓球战术行为博弈方的每一组可能的决策,都有一个结果表示该策略组合下各博弈方的所得或所失。支付是乒乓球战术行为博弈的参与人真正关心的东西。在此处应该强调的是由于乒乓球比赛计分规则的特殊性,所以博弈双方的得益可进行个多层次的划分,即一分球的得失;一局球的胜负;一场比赛的输赢。得益即参加乒乓球战术行为博弈的各方从博弈中所获得的利益,它是各博弈方所追求的根本目标,也是战术行为和判断的主要依据。乒乓球战术博弈必须对得益做出规定,得益可以是正值,也可是负值,得益是分析博弈模型的标准和基础。在乒乓球战术行为的博弈过程中,最直接的目的赢得每一分,博弈的直接结果是一分球的得失,进而变成一局球的得失,最终通过局数的得失决定整场比赛的胜负。所以,乒乓球战术行为的直接得益(一分球的得失)与战术行为的最终得益(一场比赛的胜利)存在间接性的相关关系。这里的根本目标不是前两个层次而是在第三个层次(一场比赛的胜利),因为在乒乓球项目中存在得分多并不能赢得比赛的现象[8]。
2.6 乒乓球战术行为博弈的次序(orders)
在乒乓球战术行为博弈过程中参与人即双方运动员在进行独立决策时,也就是战术行动的实施过程是有顺序、先后进行,并且不止一次地进行决策选择,乒乓球战术博弈中行动顺序对博弈结果有着非常重要的影响。在规定一个博弈时必须规定其中的次序,因为即使博弈的其他方面都是相同,次序不同一般就是不同的博弈类型,同样的参与人,同样的行动集合,行动的顺序不同每个参与人的最优选择就不同,博弈的结果就不同(事实上,不同的博弈顺序意味着不同的博弈)。特别是在不完全信息博弈中,后行动者可以通过观察先行动者的行动来获得信息,从而使得博弈分析成为预测人的行为的一个有力工具,在乒乓球战术行为博弈当中,如发球段的技战术行为实施和接发球段的技战术行为实施存在明显的差别,对博弈结果也有重要的影响。乒乓球战术行为博弈的行动是划分乒乓球战术行为博弈类型的一个重要标准(静态博弈和动态博弈)。在乒乓球战术行为博弈论中一般假定参与人的行动空间和行动顺序是所有参与人的“共同知识[9]”。
2.7 乒乓球战术行为博弈的结果(outcome)
乒乓球战术行为博弈结果是博弈分析者所感兴趣的所有东西,如乒乓球战术博弈的均衡战略组合,均衡行动组合,均衡支付组合等,从实践的角度上讲是对比赛双方运动员乒乓球战术行为运用规律的认识,有助于提高运动员的比赛获胜概率;从理论的角度讲是对乒乓球项目本质规律的深入认识,对乒乓球项目发展有着巨大的促进作用。
2.8 乒乓球战术行为博弈的均衡(equilibrium)
均衡是乒乓球战术行为博弈参与人双方的各自最优战略组成的一个战略组合。乒乓球战术行为博弈中的均衡概念包括优势策略均衡(Dominant Strategy Equilibrium)、混合策略均衡(Mixed Strategy Nash Equilibrium)、纳什均衡(Nash Equilibrium)[10]。
3 乒乓球战术行为的博弈类属研究
3.1 博弈人数
根据博弈的参与人数的多少可以分为二人博弈和多人博弈。乒乓球比赛都是双方争胜的比赛,直接表现为双方为一场比赛胜负进行战术行为的互相制约和反制约,如果是双打比赛也可把场上的同队两个队友看作一个博弈方,所以乒乓球战术行为博弈为两人博弈。
3.2 博弈次序
根据博弈行动的次序可将博弈分为序贯行动(sequential moves)和同时行动(simultaneous moves)两种博弈类型。乒乓球战术行为在实施时严格遵守时间序列,即一拍击球后(发球)接着是对手的一拍击球(接发球),接着到发球抢攻或控制(第三拍)和接发球抢攻或控制(第四拍),再到相持阶段。每个乒乓球运动员都必须思考:如果我这样做,我的对手会怎样反应?对未来结果的计算支配着乒乓球运动员当前的行动。从乒乓球战术行动的实施过程角度,乒乓球战术行为博弈应属于序贯博弈。
3.3 得益特点
根据博弈得益的特点如一方赢就是另一方输,得失总和为零,这类博弈可称为零和博弈(zero-sum games),更一般的讲,零和博弈的思想就是参与人利益完全冲突的;如果利益并不是精确为零,可称为常和博弈(constant-sum games)。乒乓球竞赛双方的利益完全冲突,一胜一负相伴而生。乒乓球竞赛中一方的得分必是对方的失分,在一分球的博弈中双方战术得益(得失分)的总和为零,在一局球、一场球的总得益(总得失分)的总和也是零。即参与竞争双方的利益完全冲突,因此乒乓球战术行为从得益(得失分)角度上应属于零和博弈。
3.4 博弈次数
在乒乓球竞赛中,并不是简短单一的一分球的争夺,而是以一分球为得益单位的多次战术行为的互动博弈,每一分球的争夺都是从发球、接发球、第三拍、第四拍……直至一分球结束,再到一局的输赢,最后才能最终决定比赛的胜负。在这里得分多并不一定能够取得比赛胜利,也是乒乓球博弈的一个特点。所以乒乓球战术行为博弈属于重复博弈,这样在持续多次的重复博弈过程中,给我们提供了分析博弈双方的战术行为“路径依赖”和博弈“纳什均衡”的可能性。
3.5 博弈信息
在临场乒乓球战术行为博弈的实施过程中,双方都了解目前的战况以及过去的过程,并且也都知道对手以赢得比赛为目标。但在此类博弈过程中,博弈双方在每个行动点上是无法获悉决策所需的全部信息的,如对手将把球回到什么位置以及怎么配套等,所以可以称这种情况为不完美信息(imperfect information)。在赛前比赛技战术行为分析时,当乒乓球博弈参与人一方比另一方了解更多信息时,这类情况称为不完全信息(incomplete information)或者非对称信息(asymmetric information)就会相应产生诡计和阴谋[11]此时乒乓球战术博弈参与人可以推测、隐藏或传递错误信息,这都是乒乓球战术博弈策略的重要组成部分。在博弈过程中参与人所拥有的信息对博弈的结果有重要的影响,当参与人拥有不同的信息时,如何操纵和信息本身就是一场博弈,甚至比后续的博弈更为重要。
3.6 博弈规则
乒乓球战术行为博弈的规则是确定的,是所有参与人必须遵守的。比赛规则包括乒乓球比赛的物质条件如球台、球网装置、球、球拍,比赛条件如场地要求等;比赛中的基本概念;比赛的胜负机制;比赛纪律等。乒乓球比赛规则保证了乒乓球战术行为博弈的公平竞争,机会均等原则。国际奥委会要尽可能地平均分布奥运会金牌的精神,国际乒联对乒乓球的竞赛规则作了一系列的重大改变:2000年10月将乒乓球比赛中一直使用的直径为38mm的乒乓球改为直径为40mm的大球,2001年9月1日将原来乒乓球的21分赛制改为11分赛制,从2002年9月1日起实行新的发球规定,也叫无遮挡发球。2008年9月,国际乒联的禁胶令颁发,奥运会后,这一禁令全面执行,乒乓球进入“无机胶水”时代。乒乓球博弈规则的每一次修改都对乒乓球技战术的使用有着非常明显的影响。
4 乒乓球战术行为博弈的表述方法
一个博弈可以用两种不同的方式来表述,一种是战略式表述(strategic form representation),另一种是扩展式表述(或者译为“展开式表述”)(extensive form representation)。尽管理论上这两种表述形式几乎是完全等价的,但从分析的方便性的角度来讲,战略式表述更适用于静态博弈,而扩展式表述更适合于讨论动态博弈[12]
4.1 乒乓球战术行为博弈的战略式表述
战略式表述又称标准式表述(normal form representation),在这种表示中,所有参与人同时选择各自的战略,所有参与人选择的战略一起决定每个参与人的支付。请注意,这里参与人“同时选择”的是战略,而不是行动。因为战略是参与人行动的全面计划,战略式表述也可以描述动态博弈[13]。
在乒乓球战术博弈过程中,参与人个数等于表的维度。显然乒乓球战术行为博弈参与人为双方运动员,所以发球-接发球博弈的博弈矩阵表的维度是二维。矩阵表中的行和列上的文字表示了两个参与人可选择的策略,所以矩阵表的规模是由参与人的策略数量决定的。表中的每个单元格列出了相应策略组合下各参与人的得益。
下面博弈矩阵表提供的信息有(如图5所示):博弈双方(发球方)和(接发球方);博弈方所拥有的策略集合为旋转发球和不转发球两种;表中前一个数字代表了博弈方的相应得益。对应的,博弈方拥有的策略集合为控制和进攻两种接发球策略;表中的后一个数字代表了博弈方的得益。
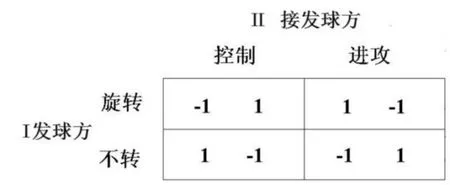
图5 发球-接发球战术行为博弈战略式表述
4.2 乒乓球战术行为博弈的扩展式表述
博弈的扩展式表述(extensive form representation)更适用于描述和分析动态博弈。博弈的扩展式表述所“扩展”的主要是参与人的战略空间。战略式表述简单地给出参与人有些什么战略可以选择,而扩展式表述要给出每个战略的动态描述:谁在什么时候行动,每次行动时有些什么具体行动可供选择,以及知道些什么。简单地说,在扩展式表述中,战略对应于参与人的相机行动规则(contingent action plan),即什么情况下选择什么行动,而不是简单的,与环境无关的行动选择[13]。
如图6给出了发球-接发球序贯行动博弈的树形图。这个博弈有两个参与人与参与人,假设参与人获得了发球权,即战术行动的发起者在图的最左端的结点(node)上表达出这个含义即发球,该结点被称作博弈树的初始结(initial mode)或者根(root)。同时也可以称作为行动结(action node)或决策结(decision node)在此结点有两个可选择的战术行为分别用“发旋转球”和“发不转球”加以标明,并用从初始结发出的枝(branch)来加以表示。现在接发球方开始在新的结点上行动了,在的结点上分别也有两个战术行为可以进行选择“控制”和“进攻”。沿着每条路径都存在一个最后的结点,即终结点(terminal node)。在该结点,所有参与人不再进行行动选择(注意终结点与行动结是不同的),表示了这些特定行动序列的结果即参与人的得益。
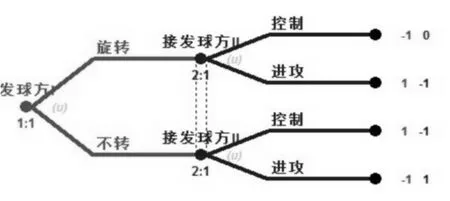
图6 发球-接发球战术行为博弈扩展式表述
5 乒乓球战术行为博弈的求解方法
5.1 战略式博弈模型的求解方法
劣策略概念及其提出劣策略涉及到博弈论的公理基础。只有在博弈论中把局中人是完全理性的共同知识尽可能的公理化(Binmore,1992),运用归纳方法为博弈论构建坚实的基础,使它成为可信赖的工具,那么博弈中局中人在个人理性假设下,可以相对定义劣策略,并且拒绝严格劣策略成为理性 选 择 的 必 要 条 件 (Weirich,1998[14,15])。 进 一 步,把Nash均衡作为非合作博弈中最基本的解,才会有两个基本结论:①严格剔除劣策略过程中不会消去Nash均衡;②重复剔除劣策略过程后剩下的最后唯一的策略组合(即重复剔除的占优均衡)是Nash均衡。事实上,重复剔除严格劣策略是均衡的精炼(即对概念详细区分的)过程(武康平,2001)。所以重复剔除劣策略成为分析博弈和寻找Nash均衡的基本方法之一。在围绕博弈论基本概念发展中,D.Berhemi(1984)和D.Pearce(1984)在假设局中人是贝叶斯优化者为共同知识假设下导出了被占优策略的重复剔除。占优策略均衡、重复剔除的占优均衡、Nash均衡在非合作博弈论中作为主要的概念其关系也得到了揭示(张维迎,1996[16,17]。
5.2 扩展式博弈模型的求解方法
极小极大算法(minimax algorithm)是为博弈中的一方寻找一个最优行动方案的方法[18]。为了找到当前的最优行动方案,需要对各个行动方案可能产生的后果进行比较。具体地说,就是要考虑每一方案实施后对方可能采取的所有行动,并计算可能的分值。为计算分值,需要定义一个估值函数,用来估算当前博弈树叶节点的分值。当叶节点的估值计算出来后,再推算出父节点的分值。推算的方法是,对于“或”节点,选其子节点中一个最大的分值作为父节点的分值,这是为了使自己在可供选择的方案中选出一个对自己最有利的方案;对于“与”节点,选其子节点中一个最小的分值作为父节点的分值,即考虑最坏的情况。如果一个行动方案获得较大的倒推值,则它就是当前最好的行动方案。为了表述方便,我们将取极大值的一方称为Max方,另一方称为Min方。
6 结 论
6.1 乒乓球战术行为博弈理论,即是关于乒乓球战术行为合理运用的理论体系,是研究如何在乒乓球竞赛实践中战胜对手,提高胜算,获取比赛优胜的理论。乒乓球战术行为博弈理论是以“博弈论”的基础理论、思想方法去研究和探索乒乓球技战术在竞赛过程中合理运用的微观问题的理论,探讨在乒乓球运动竞赛中如何去战胜对手、提高胜算、获取优胜的科学理论。
根据乒乓球比赛规则和战术行为的交叉效应,乒乓球竞赛战术实施过程可以表示为相互作用的耦合系统。
6.2 乒乓球战术行为博弈要素包括:参与人(players)、行动(action or moves)、信息)(information)战略(strategy)、支付(payoff)、次序(order)结果(outcome)和均衡(equilibrium)。对一个乒乓球战术行为博弈描述至少必须包括参与人、战略和支付,而行动与信息则是建筑材料。参与人、行动、次序和结果结合起来称为乒乓球战术行为博弈的规则(rules of the game),我们的研究目的在于运用博弈的规则来确定并分析乒乓球战术行为博弈的均衡。
6.3 乒乓球战术行为的博弈类属可从不同角度出发进行分类,从博弈的参与人数量角度上乒乓球战术行为博弈是两人博弈;从博弈的次序角度上可定义为序贯博弈;从博弈的得益特点角度为零和博弈;从博弈的次数角度为重复博弈;从博弈的信息角度可定义为完美但不完全信息博弈,乒乓球战术行为博弈有着特定的博弈规则,双方运动员必须遵守,并且规则对战术行为的实施有着非常明显的影响。乒乓球战术行为的博弈类属是确定其纳什均衡的基本前提。
6.4 根据乒乓球战术行为实施的特征,乒乓球战术行为博弈模型的建构,可有两种表示方法,如把战术行为的博弈过程,看作是纯策略同时行动博弈,那么就可以用博弈表也称博弈矩阵或支付表来进行描述。如果把乒乓球战术行为博弈中战术行为博弈看作是序贯博弈,可以用博弈树进行表示。这种树型图被称作博弈的扩展式表示方法。
[1]李光久.博弈论基础要点注释与题解精编[M].南京:江苏大学出版社,2008:32-46.
[2]迪克西特·斯克丝.策略博弈[M].蒲勇健,等译.第二版.北京:中国人民大学出版社,2009:68-74.
[3]李益群,谢亚龙.体育博弈论[M].北京:北京体育大学出版社,2002:8-21.
[4]张晓蓬.中国乒乓球队战术训练水平定量诊断方法及实践效用[D].中国优秀博硕士学位论文全文数据库(博士),2004:25-36.
[5]张辉.球类比赛计算机诊断与分析[M].哈尔滨:黑龙江科学技术出版社,2006:165-181.
[6]Shapley,Lioyd S.A Palue for N-Person Games[J].grinceton University Press,1953(28):307-17.
[7]唐建军.乒乓球运动教程[M].北京:北京体育大学出版社,2005:42-86.
[8]张辉,霍赫曼·安德烈亚斯.球类比赛数学模拟诊断的理论与实践[J].体育科学,2005(11):3-5.
[9]G.Debreu,H.Scarf.A linit theorem on the core of an economy[M].International Economic Review,1963:235-246.
[10]Von Neumann,J.,Morgenstern Oskar.Theory of games and economic behavior[M].Princeton,1944:178-185.
[11]D.Kreps,R.Wilson.Sequential equilibria[M].Econometrica,1982:863-894
[12]R.Selten.Reexamination of the perfectness concept for equilibrium points in extensive games[J].International Journal of Game Theory,1975(4):25-55.
[13]谢识予.经济博弈论[M].上海:复旦大学出版社,2002:9-31.
[14]Ken G.Binmore.A text on game theory[J].Published Simultaneously in Canada,1992(4):8-12.
[15]Weirich,Paul.Game theory revised by decision rules[J].Cambridge University Press,1998(2):7-10.
[16]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2004:27-38.
[17]约翰·纳什[美].纳什博弈论论文集[M].张良桥,王晓刚,译.北京:首都经济贸易大学出版社,2000:56-64.
[18]王骐.博弈树搜索算法的研究及改进[D].浙江大学,2006:25-32.
——博弈论

