流速仪比较与林边溪流量量测

江介伦，杨翰宗，吕育轩，吴佳颖，简志耿

（1.屏东科技大学 水土保持系，台湾 屏东912；2.树德科技大学 休闲事业管理系，台湾 高雄824）

台湾地势陡峻，河川短促，造成河川流量变化大，因而河川水文资料的观测、搜集、调查工作格外困难，水文基本资料系水资源开发利用、防灾预警及水利工程规划设计最重要之规划依据，而流量观测一直是台湾水文技术上亟待突破之课题[1]。河川流量是研究水文现象的主要因子之一，目前较常使用的流速仪大多为机械式的，故取电磁式流速仪、超声波数位流速仪及旋杯式流速仪，分别比较机械式和非机械式的仪器实测差别和实用性。

河川的通水断面积、流速、流量、河川深度及河道宽度等会因丰水期与枯水期变化量大，每条河川皆有不同的特性，藉由实地测量之数据，进而分析林边溪来义大桥附近之流量与通水断面积、河川深度及河道宽等的关系式，以提供水利工程做为参考数据。

1 研究背景

流速测量一直是水利工作中很重要的一环，杨翰宗等人[2]利用手持式声波杜普勒流速仪和旋杯式流速仪进行低水位时期之流量测定，比较两种量测仪器的优缺点及其所测得之流量，显示手持式声波杜普勒流速仪可准确测得流量，且仪器携带以及安装非常便利，并可大幅缩减整个流量的量测时间。许盈松等人[3]曾分别针对旋杯式流速仪与旋桨式流速仪，依据ISO3455规范进行校正试验工作，并对量测值进行回归分析、器差分析及不确定度分析。归纳评估此两种常用转子式流速仪之器差及不确定度分析差异，可明显看出旋杯式流速仪在流速低于0.5m／s条件下之灵敏度及器差表现皆较佳。黄宏斌等人[4]针对电波流速仪与旋叶式或电磁式流速仪于渠槽试验中测出之表面流速，利用所测得之水流点流速值进行分析，得到电波流速仪观测清水流况下的河川之修正系数，以及平均流速与表面流速间之回归关系式。谢志能[5]收集曾文溪及高屏溪主流及其支流上水文站的实测流量资料，所收集之资料为流量及河道相关断面资料进行分析，得到流量和断面积在河川自然的冲淤下，仍符合流体力学的连续方程序；自然河床属动床，故在河床冲淤变动下，流量与水面宽度、水力深度之相关性较差。王瑞德[6]探讨人工渠道及自然河道的水力半径R及水力深度D 之比值α（R／D）。以曾文溪及高屏溪为例，分析自然河道α值的特性，其曾文溪α值为0.70～0.95，高屏溪α值为0.80～0.95。

2 量测方法

2.1 流速量测方法分类

流速测量依接触水体与否主要可以分为接触式与非接触式[7]。（1）接触式。流速计最常使用的螺旋流速计是普来式流速计（Price current maters），通常以一点法或二点法量测平均流速，量测时可由桥梁上、船上或架设索道施测，每一点量测至少须超过40 s；浮标量测法适用于多数的洪水流况，水流急且气候恶劣，流速计难以施测的情况下，利用浮标量测水面流速计算平均流速的方式；声波都卜勒流速剖面仪主要是依据都卜勒原理，利用声频侦测水体中随水流移动之悬浮微粒散射回波的频移，以量测水中流速，同时经由底床回波反射量测水深。

（2）非接触式。流速影像量测方法是依据影像撷取器架设的位置可分为卫星航照、航空摄影及地面摄影等，一般卫星航照由于高解析度影像不易取得且机动性不足所致，卫星影像在洪水量测上大多应用于淹水区的量测与分析，而用于水面流场量测主要是利用航空与地面摄影两种方式；微波雷达表面流速仪是使用连续波雷达做为量测机制，通常可将其架设于桥梁上量测水面速度。但由于其仅能从事单一固定测点的速度量测，经由率定横向及垂向平均流速之转换系数，计算断面平均流速与流量。

2.2 流量计算法

流量计算一般有中断面法与平均断面法，本研究采用平均断面法估算流量。此法系将河川分为数个断面，其水深分为d1，d2，d3，…，宽度为b1，b2，b3，…，各断面平均流速为v′n＝（vn＋vn＋1）／2，则通过河川断面之流量即为各部分流量之总和。

3 仪器介绍

研究所使用三台仪器之特性如表1所示。

表1 仪器之特性

3.1 电磁式流速仪（简称FP111）

量测时将螺旋桨放入水中，水流带动涡轮使摩擦很小的轴转动，旋叶上的磁性金属在涡轮转动时会产生电信号脉冲，通过转换装置可以将转速转换成水流速度并显示在手柄屏幕上（图1）。

3.2 超声波数位流速仪（简称ADC）

ADC发出一超声波，而这个超声波将被水中的悬浮颗粒反射。通过DSP（数位信号处理器）处理，反射后的回声图像取决于粒子大小与形状。再过一段短的时间间隔后，仪器发出第二超声波，第二幅回声图像亦相同处理。

根据DSP的量测相位，利用交叉关系方法（Cross Correlation Method）比对两个时间差的反射图像，这种方法随着时间位移，去除所有不同的讯号，保留两幅相似的图像，用于计算水流速度并显示于LCD屏幕上（图2）。ADC的量测点，位于量测探头前端，大约10～15cm的距离处。

3.3 旋杯式流速仪（Price type AA meter）

旋转杯受流水冲击而转动，其回转数经由发数位计数器显示，并配合所经时间之量测，最后根据流速与转速公式求得水流流速（图3）。

公式一般表示为：V＝aN＋b，其中V＝流速（m／s）、N＝旋杯旋转次数（r／s）、a及b为率定常数，而率定后之常数与计算公式为：V＝（2.2048 N＋0.0178）×0.3048＝0.672 N＋0.0054

图1 电磁式流速仪

图2 超声波数位流速仪

图3 旋杯式流速仪

4 研究区概况

林边溪位于屏东县境內，东经120°28′—120°40′，北纬22°20′—22°30′，河长约42.19km。流域面积约336.30km2，发源于中央山脈之南大武山西南麓，主要支流包含瓦鲁斯溪、大后溪、来社溪、尖刀尾溪、七佳溪、力力溪等，主流流经泰武乡、来义乡、新埤乡、佳冬乡、林边乡，在佳冬乡和林边乡交界流入台湾海峡。本次研究区域选定在来社溪与林边溪之交接处，位于来义乡来义大桥附近，现地状况如图4所示。

图4 来义大桥下游河床现况

5 结果与分析

于林边溪同时间同测点ADC与FP111，测得11场之平均流速比较，FP111所测数值较ADC大，见图5，以ADC所测流速为基准，其平均误差率为8.17%。

利用2010年8月到2011年2月共实测22场流速实测数据计算出湿周（P）、河道断面积（A）、水力半径（R）、水面宽度（T）、水力深度（D）和流量（Q），分别比较其相关系式，以及的R／D＝α值之趋势，流量计算方法取平均断面法计算，因其与实际地形颇为相符且准确性较高。而林边溪之α值（R／D）之趋势如图6所示，皆大于0.9。

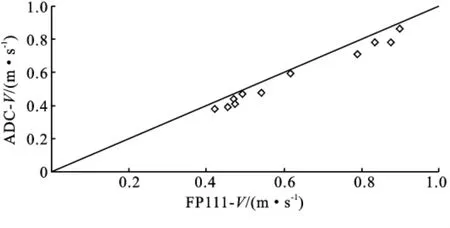
图5 ADC与FP111流速比较

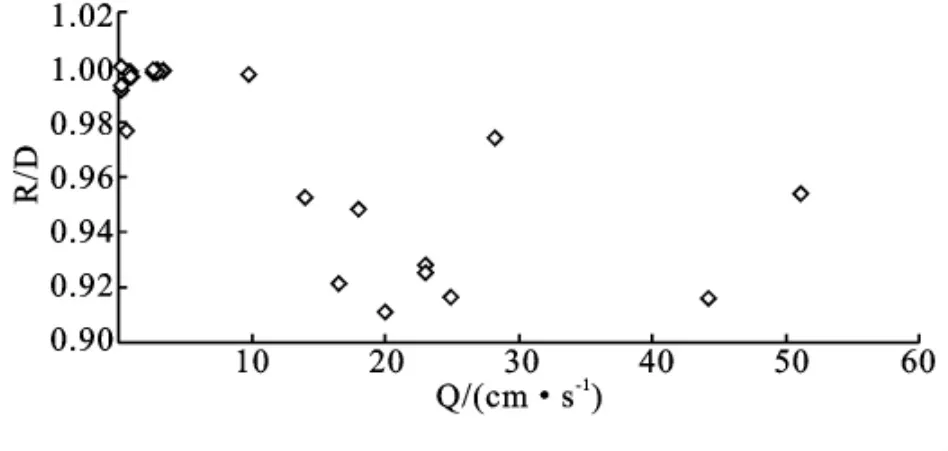
图6 流量与α值的关系

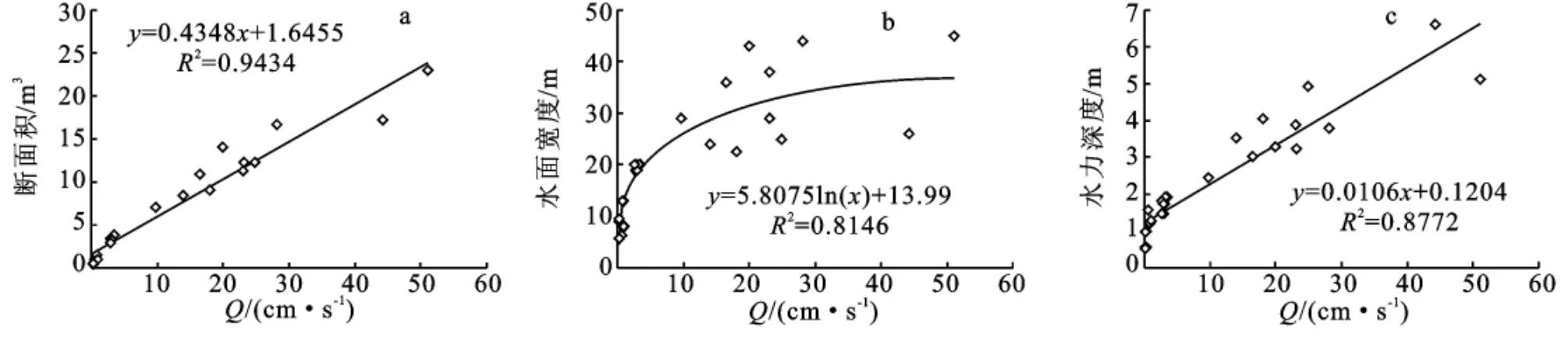
图7 流量分别与（a）通水断面积（b）水面宽度及（c）水力深度的关系

而流量Q与通水断面积A之关系如图7a显示流量Q与通水断面积A之相关性非常良好，判别系数R2高达0.9434。图7b显示流量Q与水面宽度T之关系，当流量Q＞10cm／s时以后，流量Q与水面宽度T之测点开始散乱，相关性有越来越差趋势。图7c显示出流量Q＞10cm／s以后，流量Q与水力深度D之相关性有越来越差趋势，此与流量Q和水面宽度T之关系相似。

6 结论

（1）α值（R／D）和流量Q 大约在0.911～1之间，而流量Q＜10cm／s时，α值非常趋近于1，当流量Q＞10cm／s时，α值大约在0.91～0.96，当得知河断面α值与较易量测的水面宽度T，则湿周可由P＝T／α推算出。

（2）流量Q与通水断面积A有极高的关系性（R2＝0.9434）符合Q＝AV之物理特性。Q，T之关系式与Q，D之关系式都有流量Q＞10cm／s时以后，相关性有越来越差的趋势，故流量Q＞10cm／s时水面宽度T及水力深度D的改变量较大。

（3）一般机械式仪器进行低水位量测时，螺桨常因为流速太小导致无法克服磨擦力而转动，或被一些小石子卡住螺桨不能转动，而影响仪器量测之精度。

（4）超声波数位流速仪水深只要可以淹没量测探头，即可进行流速之量测，应用于浅水测量流速为相当实用之仪器；高水位高流速时为考量测量人员之安全性，以垂吊方式量测的旋杯流速仪为首选 。

（5）整个实测纪录中，当水流流速非常微小的时候（即流速为0.01m／s时），只有ADC依旧可将这些微流速量测出来。

（6）整体比较下超声波数位流速仪稳定性良好、量测精度高且在量测探头下有压力计可直接由显示屏幕上读取水深操作简易方便等特性，明显的超声波数位流速仪优于机械式的电磁式流速仪及旋杯流速仪。

[1]许盈松，刘杰立，张国强.流量观测不确定度评估：以浊水溪溪洲大桥站为例[J].台湾水利季刊，2004，52（1）：72－82.

[2]杨翰宗，陈彦章，郭振泰，等.应用手持式声波杜普勒流速仪量测低水位时之流量[J].台湾水利，2008，55（4）：21－32.

[3]许盈松，蔡俊锋，周湘俊，等.旋杯式与旋桨式流速仪观测特性分析研究[J].中华水土保持学报，2007，38（2）：185－194.

[4]黄宏斌，谢孟荃，电波流速仪与旋叶式流速仪于清水流之流速观测研究[J].中华水土保持学报，2007，36（1）：69－88.

[5]谢志能.曾文溪及高屏溪流量关系式之研究[D].台湾台南：成功大学，2003.

[6]王瑞德.水力半径和水力深度比值之研究[D].台湾台南：成功大学，2003.

[7]李明静.河川表面流速与流量非接触式量测方法之发展及应用[D].台湾台南：成功大学，2003.