基于积温变化的水稻叶形态伸展过程可视化模拟

孙爱珍，何火娇，杨红云，唐建军，罗 威

(江西农业大学 软件学院/江西省高等学校农业信息技术重点实验室，江西 南昌 330045)

叶片是水稻作物光合作用的主要器官，其几何形态结构是研究三维虚拟水稻生长系统的重要组成部分，水稻主茎每出生一叶片都会形成、生长相应的器官，因此，可根据叶龄预报分蘖发生、节间伸长时间、成穗与穗分化进程。目前，国内对虚拟作物的研究，大多集中对作物形态结构进行三维可视化或者对作物的生态生理机制过程进行建模［1－7］，很少量化作物形态结构变化规律与环境和技术措施之间的动态关系，因此不能很好地可视化模拟实际生产条件下植物形态结构的动态变化过程。在系统研究方面仍未出现较成熟的作物虚拟生长系统，水稻虚拟动态生长的研究报道还很少。

本文通过分析水稻主茎叶片形态参数受环境温度影响的动态变化规律，分别构建了叶位有效积温模型、叶位与叶长关系模型、叶长有效模型、叶长与叶宽关系模型、茎叶夹角变化模型等水稻叶片几何形态生长方程。根据实测水稻叶片的形态数据和图形学知识构建了叶片三维模型。由叶片形态积温关系模型可确定水稻叶片生长周期中有效积温t时刻的几何形态特征，结合叶片三维形态模型，重构叶片的真实三维空间形态。系统采用VC++编程语言，结合OpenGL图形函数库和计算机图形技术在微机上实现了水稻叶片形态生长过程的可视化模拟。研究结果将为进一步构建虚拟水稻生长系统提供参考。

1 材料与方法

本研究主要以水稻叶片器官形态结构动态变化过程为研究对象，水稻栽培实验采用江西地区推广种植的杂优品种金优402，试验于2010年和2011年在江西农业大学校内实验站进行，水稻播种时间为05月20日，06月02日正式测量，测量周期为06月02日—08月22日，水稻样本采用常规方式进行栽培和管理。每天对水稻器官形态参数(主要是叶片)进行测量。从出苗开始，每天定点进行观测。从主茎第二叶片露尖(没露尖时，叶片卷曲为针形)开始每天测量一次，直至叶片定长。测量的参数包括叶片的长度、最大叶宽、茎叶夹角。另外利用三维数字化测量仪测量叶片从叶枕到叶尖处叶脉曲线上离散的5个点坐标，叶片定长后，在同一张叶片上，每间隔2 cm测量一个叶宽值，供叶片形态三维建模使用。同时记录下每天测量的叶片位置次序和温度数据，温度取值为每天08:00、12:00和18:00的平均温度。

2 叶片形态积温关系模型

2．1 叶位有效积温模型

试验研究表明，水稻主茎不同叶位叶片出生的速率有所差异，前3叶的叶片出生相对缓慢，从第4叶到第8叶叶片出生速率相对较快，而第9叶以后叶片的出叶速率逐渐下降，其变化过程如图1所示。

叶位有效积温模型可用方程(1)来描述。

其中，n为叶位序号，t为有效积温(每天的平均温度减去水稻生长下限温度10℃之后的累加和)。其中参数 a= －3．2，b=16．1，c=389．0，d=252．8。

2．2 叶长与叶位关系模型

试验研究表明，水稻主茎不同叶位叶片定型后的长度(Lleaf)随叶位呈线性变化［8］如图2所示，可用方程(2)定量描述。

式中，Lleafn为第n叶位的最终叶长，a、b为方程系数，本试验中分别取a=4．945 5，b= －2．918 2。

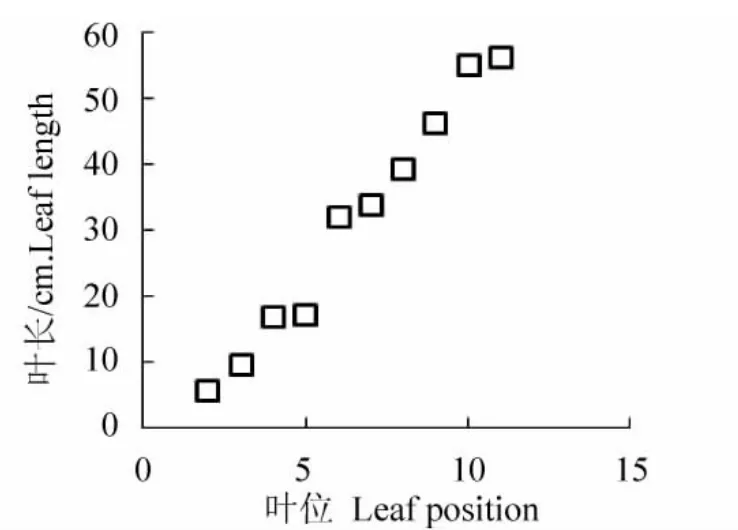
图2 叶长与叶位的关系Fig．2 Relationship between leaf length and leaf position

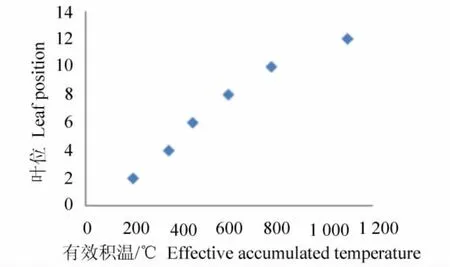
图1 叶位与有效积温关系Fig．1 Relationship between leaf position and effective accumulated temperature

2．3 叶长有效积温模型

叶长和叶宽是水稻叶片形态的两个主要属性。图3展示了水稻主茎不同叶位叶片长度归一化值(叶长与叶片定长长度相除的值)随有效积温递增的动态变化过程。可以看出，水稻叶片伸长是一个由

公式中，ILlfn(t)定义为第n叶片露尖后有效积温为t时的归一化值，记第n叶片在有效积温t时的长度为Llfn(t)，则Llfn(t)等于该叶最终叶长Lleafn与归一化值ILlfn(t)的乘积，a和b为方程系数，通过不同叶位与系数的数据拟合表明，方程系数可用公式(4)和公式(5)来描述。

(4)、(5)式中 k1，k2，k3，k4为公式(4)系数，p1，p2，p3为公式(5)的系数，本实验中取值为:k1=91．56，k2= －0．707 8，k3=0．253 5，k4=0．248 3，p1=0．000 841 7，p2= －0．013 11，p3=0．057 25。慢至快再到慢的变化过程，最后叶片定长，在衰亡前叶片长度基本维持不变，符合S型曲线即Logistic方程。

对水稻叶片叶长伸长过程可用方程(3)来描述:

2．4 叶宽与叶长关系模型

在水稻叶片伸长过程中，叶宽的潜力就基本确定了［5－6］。可以看出，叶片抽出后，4～5 d时间叶片就展开，叶宽变化差异不显著，叶宽随叶长的变化如图4所示。叶片在伸长的过程中，叶长与叶宽的关系呈二次曲线变化，可用方程(6)描述。

(6)式中，Wlfn(t)为有效积温t时叶片最大宽度，Llfn(t)为有效积温t时的叶长，p1，p2，p3为方程系数，根据试验资料，分别取值为 p1= －0．000 278，p2=0．056 07，p3= －0．141。

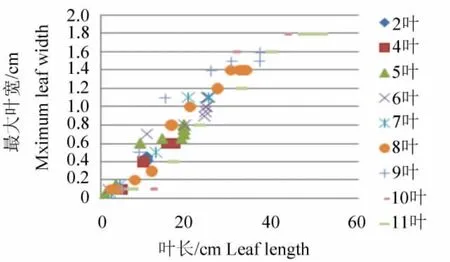
图4 叶长与最大叶宽的变化规律Fig．4 Leaf length and maximum leaf width variation

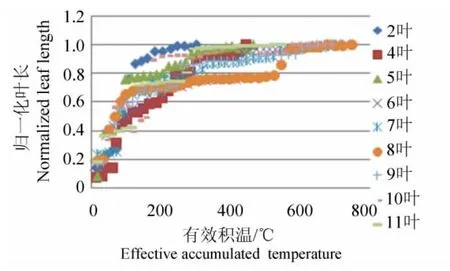
图3 叶长有效积温的动态变化规律Fig．3 Normalized leaf length with the dynamic changes of effective accumulated temperature

2．5 茎叶夹角变化模型

叶片生长过程中，茎叶夹角的变化可分为四个阶段［9］。第一阶段从n叶叶片露尖至完全伸长(n+1叶抽出前)茎叶夹角变化不大，一般可近似为0;第二阶段在n+l叶抽出过程中，n叶茎叶夹角变化与叶片伸长同时进行，由试验结果可知，该阶段不同叶位叶片夹角与长度呈幂函数变化，当n+l叶进入伸长未期时，叶茎叶夹角定型;第三阶段，在n叶位产生分蘖前，n叶茎叶夹角变化不大，当叶位产生分蘖时，n叶片与分蘖茎夹角变化不大，但随着主茎与分蘖茎的夹角增加，叶与主茎的夹角又进一步增加，约1个叶龄期后，分蘖茎与主茎的夹角定型，n叶与主茎的夹角又维持不变，直至叶片衰亡始期。第四阶段，叶片衰亡后，随着干物质输出，叶鞘枯死、腐烂，茎叶夹角进一步增加，直至叶片完全死亡。对于拔节后的叶片形态仅包括前两个阶段。分蘖和主茎的夹角(即阶段3和阶段4)的角度变化在分蘖模型中处理，在本实验中前两阶段中茎叶夹角变化可用公式(7)表示:

(7)中θn为第n叶的茎叶夹角，Llfn(t)为有效积温t时的叶长，a，b为方程系数，根据本实验结果，b取值为1．19，系数a的值与叶位顺序呈线性关系，见方程(8)描述。n表示叶位，k1，k2为方程系数，取值分别为 －0．113 8 和1．22。

2．6 模型的检验

模型检验利用试验数据，采用常用的均方根差法(RMSE)对模拟值与观测值的符合度进行统计分析，RMSE值的计算如方程(9)式:

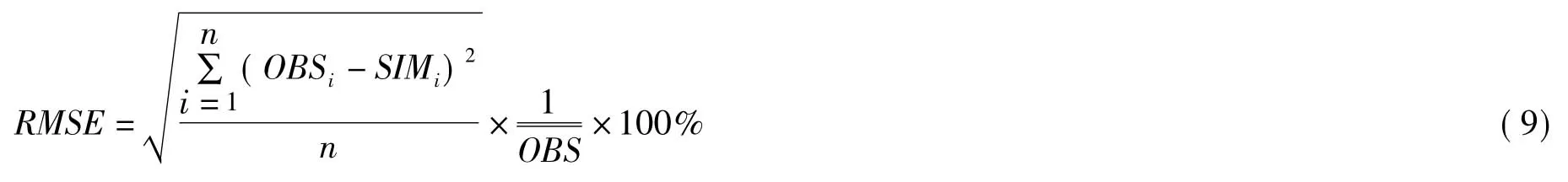
(9)式中，OBSi和SIMi分别为观测值和模拟值，OBS为观测值的平均值，n为样本容量。RMSE能很好的反映模型模拟值的预测性，RMSE值小于10% ，表明模拟值与实际观测值一致性非常好，10% ～20%比较好，20% ～30%表明模拟效果一般，RMSE值大于30%表明模拟值与实际值偏差大，模拟效果差。根据建立的模型和实验数据，计算各水稻叶片形态生长模型的RMSE值如下表所示:

表1 水稻叶片形生长方程模型RMSE值Tab．1 RMSE of rice leaf growth model

从上述模型检验计算的RMSE值可以看出，在常规栽培模式下，采用有效积温建立的水稻叶片形态生长方程构建叶片形态几何参数模型，模型模拟值和观测值有较高的吻合度和可靠性。

3 叶片三维形态模型

3．1 叶片边缘曲线

通过对水稻叶片的观测分析，利用三个控制点的Bezier曲线可以较好地模拟平滑的叶片边缘。在xoy平面上，假设水稻叶片的叶长为LL，最大叶宽为LW，则描述叶子上叶边缘的Bezie曲线的的三个控制点的的坐标:(0，0)，(LW，LL/2)，(0，LL)，描述叶子下叶边缘的Bezie曲线的的三个控制点的的坐标:(0，0)，( － LW，LL/2)，(0，LL)。

叶片实际扫描图片以及在OpenGL生成的叶片边缘曲线控制点及其三角网格化效果如图5所示。

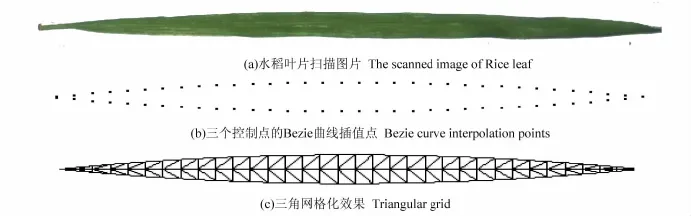
图5 扫描叶片、Bezier曲线插值生成的叶片边缘控制点和三角网格化的效果Fig．5 Sanned image，the leaf edge of the control point and the triangular grid based on Bezier curve interpolation

3．2 叶片的坐标信息

将利用Bezier曲线插值获得的水稻叶片边缘轮廓点坐标分上下两部分，上边坐标信息存入(UXi，UYi)数组，下边坐标信息存入(DXi，DYi)数组。叶片中脉坐标(MXi，MYi)可近似等于上下坐标之和的一半，即MXi=(DXi+UXi)/2，MYi=(DYi+UYi)/2，叶半宽度Hwdi=(UYi－DYi)/2，其中i的范围:0≤i＜MaxNum，MaxNum为叶片边缘取点个数。

3．3 三维叶片模型

由于在自然环境中生长的水稻叶片往往是三维弯曲的曲面形状，将叶片的中脉曲线旋转到二维平面上(设为xoy平面)，在叶片不发生折断的情况下，可认为叶片中脉曲线一阶可导、二阶连续。通过对不同叶位的水稻叶片测量的数据分析，三维叶片中脉曲线方程可用叶片的形态参数组成的二次曲线方程(10)来表征。

(10)式中LW为最大叶宽，LL为叶长，k为调整系数，θ为叶倾角(θ=π/2－茎叶夹角)。

将叶中脉曲线等分为n等份，每段的长度均为LL/n，设叶中脉曲线起点在坐标原点。起点(MX0，MY0，MZ0)坐标为(0，0，0)。根据叶中脉曲线方程按等分段顺序可分别计算水稻叶片叶中脉点和对应叶片上下边缘点在三维空间的位置坐标:

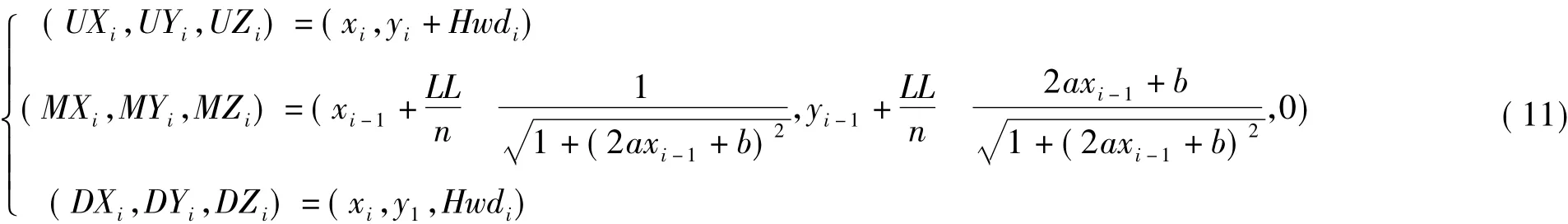
(11)式中 a=k×LW/LL，b=tanθ。

根据公式(11)，在OpenGL中计算并绘制出叶片的弯曲三维形态，通过调整系数k以及旋转变换等操作可以很方便地实现水稻叶片任意方向和角度的弯曲变换。等分数n值越大，模拟叶片的边缘和曲面越平滑。三角网格化叶片三维空间弯曲效果如图6所示，其中(a)为弯曲三维效果，(b)为叶边缘点绕中脉线旋转一定角度，实现了叶片的扭曲三维效果模拟。

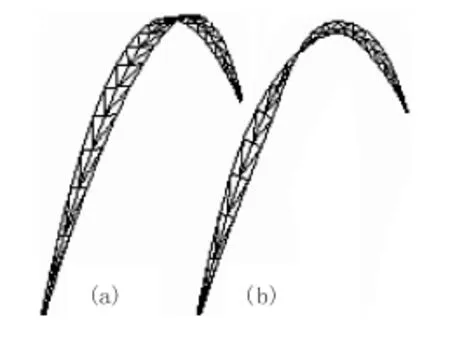
图6 弯曲和扭曲叶片三维形态Fig．6 Bending and twisting three-dimensional shape of leaves

4 系统可视化实现

在水稻生长过程中，由叶位有效积温模型计算叶片出叶的顺序，由叶位与叶长关系模型确定不同叶位叶片的最终叶长，由最终叶长和叶长有效积温模型计算出该叶片在有效积温达到t时刻的叶长，有叶长叶宽关系模型计算得到叶片对应的宽度，再根据茎叶夹角模型确定叶片与主茎的夹角，由此可确定水稻叶片生长周期中有效积温t时刻的几何形态特征;根据叶片几何形态参数和叶片三维形态模型，计算有效累计积温t时刻的叶片三维空间形态。结合OpenGL图形函数库，采用VC++在计算机上设计并开发了虚拟水稻生长系统。图7为计算机上绘制的叶片生长过程中其形态动态变化可视化效果图，根据水稻叶片形态积温关系模型的输出结果，结合水稻植株分蘖拓扑结构和水稻其它器官的形态模型［10－12］，在计算机上模拟水稻植株穗前分蘖随有效积温动态生长过程的可视化效果如图8所示，加入了光照模型，真实感强。

图7 叶片随有效积温伸展过程Fig．7 Process of growth changes leaf

5 结论

本文通过系统分析常规栽培方式和管理方式下水稻主茎上不同叶位叶片的叶长、叶宽、叶位和茎叶夹角等形态指标与有效积温的动态变化规律，并以有效积温为时间尺度，解析和提炼出水稻叶片几何参数变化的动态规律和定量算法，构建了水稻叶片几何形态动态生长方程模型。同时，分析叶片形态参数数据，结合叶片器官空间伸展形态，重建了水稻叶片三维模型。利用计算机图形学技术和面向对象编程技术实现了水稻植株穗前形态结构变化过程的可视化表达，为进一步进行虚拟水稻生长研究奠定了良好的基础。

本模型只是分析了常规栽培条件下叶片伸长过程受环境温度变化生长规律，而水稻叶片生长过程还会受到不同环境因子的制约，如肥料、水分、光照和病虫为

害等。因此，今后的研究要进一步拓展模型的适用性，研究水稻器官形态生长变化与其生长环境因子之间的耦合机制与方法，实现形态结构模拟与生理生长过程模拟的协调与统一，进一步提高虚拟水稻生长系统的普适性。

图8 水稻植株穗前形态动态生长过程Fig．8 Dynamic growth process before heading of rice plants shape

［1］管鹤卿，廖桂平，李锦卫．虚拟植物的研究内容及实现技术综述［J］．农业网络信息，2006，21(12):42－46．

［2］范振岐，司春景，胡超越，等．虚拟植物技术的研究综述［J］．安徽农业科学，2012，41(1):577－578．

［3］郭新宇，赵春江，肖伯祥，等．玉米三维重构及可视化系统的设计与实现［J］．农业工程学报，2007，23(4):144－148．

［4］赵春江，郑文刚，郭新宇，等．玉米叶片三维形态的数学模拟研究［J］．生物数学学报，2004，19(4):493－496．

［5］常丽英，张文宇，曹卫星，等．水稻叶色变化动态的模拟模型研究［J］．作物学报，2007，33(7):1108－1115．

［6］陈国庆，朱艳，曹卫星．小麦叶鞘和节间生长过程的模拟研究［J］．麦类作物学报，2005，25(1):71－74．

［7］李磊，刘晓东，罗轶先，等．基于控制点的玉米雄穗生长形态建模［J］．计算机工程与应用，2004，40(9):203－205．

［8］杨红云，孙爱珍，何火娇，等．水稻叶片形态日变化过程可视化模拟研究［J］．计算机工程与应用，2009，45(36):170－173．

［9］石春林，朱艳，曹卫星．水稻叶片几何参数的模拟分析［J］．中国农业科学，2006，39(5):910－915．

［10］刘桃菊，唐建军，戚昌瀚．水稻形态的分形特征及其可视化模拟研究［J］．江西农业大学学报2002，24(5):583－586．

［11］杨红云，孙爱珍，何火娇，等．水稻稻穗可视化模拟研究及其实现［J］．安徽农业科学，2008，47(5):1732－1733．

［12］杨红云，罗威，何火娇，等．水稻主茎三维形态建模与计算机模拟［J］．江西农业大学学报，2008，30(6):1153－1156．