基于ANSYS 的脚手架钢管的屈曲分析
于兆清 王春光
(招金矿业股份有限公司夏甸金矿,山东夏甸 265414)
近几年来,我国的建筑业蓬勃发展,为我国的经济发展做出了重大的贡献;同时,施工现场的安全生产事故也是屡见不鲜,其中有一类事故比较常见,这就是脚手架坍塌事故。据统计[1]:2010年我国脚手架坍塌事故总共发生12起,造成了极大财产损失。脚手架坍塌的事故原因有很多种,其中主要原因为支撑失稳。本文仅就局部弯曲导致的失稳进行分析。
脚手架工程常用的钢管规格为φ48×3.5,其截面计算参数见表1。

表1 φ48 ×3.5 钢管截面计算参数[2,3]
1 计算杆件的选择[2]
本次计算选择工程常见的杆件:计算长度为3.6 m,设计强度为 f=205 N/mm2,长细比 λ =l0/i=360/1.58=227.9,中心受压折减系数 φ=0.14,从而得:承载力[N]=φAf=0.14×489×205=14 034.3 N。
2 杆件ANSYS有限元计算模型
在模型中,使用Beam189单元模拟该杆件,两端均为铰支。杆件的ANSYS有限元模型如图1,图2所示。

图1 有限元模型
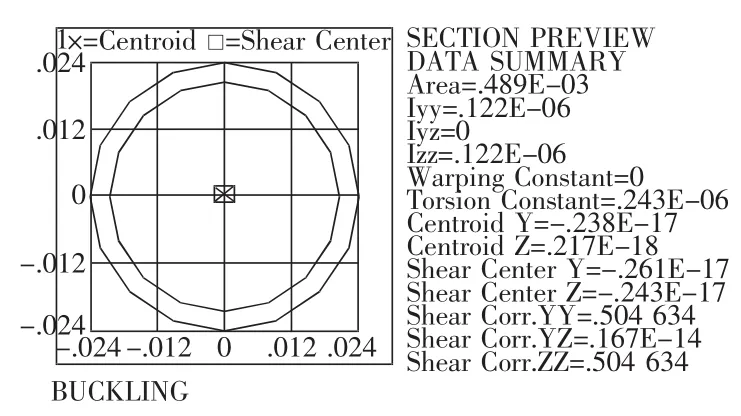
图2 杆件截面理论计算参数
3 特征值理论计算
关于杆件失稳临界力的计算已有相应的经典理论计算公式。

通过式(1)的计算得出特征值计算值为19.47 kN。
4 特征值屈曲计算
特征值屈曲计算主要针对没有初始缺陷的构件,得出在特定工况下杆件发生失稳的理解值,以及与此值相应的屈曲模态。通过对上述模型的计算得出该杆件的第一模态特征值为19.71 kN,即失稳临界力为19.71 kN。
通过特征值模拟值与计算值的比较,两者相差不足1.5%,误差很小,这说明模型是合理的。
5 非线性屈曲分析
由于各种原因,施工现场脚手架工程使用的钢管有的可能有初始弯曲,这势必会导致理论计算值与实际值不符,从而无法判断实际受力状态。下面就不同程度的初始缺陷进行分析,得出不同程度初始缺陷所产生结果的规律性。
分别取特征值屈曲分析第一模态的 0.05,0.045,0.04,0.035,0.03,0.025,0.02,0.015,0.01,0.005,0.001 为杆件的初始缺陷进行计算分析,得出如下结果,如图3,图4所示。

图3 不同程度初始缺陷对极值点的影响

图4 各缺陷对应极值比特征值降低程度
通过图3我们看到随着初始缺陷程度的增大,极值点随之下降;曲线与二项式y=2 450x2-291.57x+19.359拟合的很好。在实际应用时可采用该二项式对实际受力情况进行判别。
通过图4我们发现随着初始缺陷的增大,极值点下降程度急剧增加;曲线与二项式y=-12 583x2+1 497.5x+0.572 1拟合的很好。当初始弯曲为1%时,降低程度达到15%,这个降低值是相当可观的。
通过杆件承载力与图4的对比,可以得到:当初始缺陷达到2%时,实际极限承载力与杆件计算极限承载力相差不过3%,相当接近;当初始缺陷达到2.5%时,实际极限承载力已经比杆件计算极限承载力低,这是非常危险的。
6 结语
通过对该杆件的稳定性进行有限元模拟,我们得到如下结论:
1)初始缺陷对于杆件的失稳状态影响很大;2)在施工时,应尽量选取初始缺陷小的构件作为压杆;3)当不可避免的需要使用初始缺陷较大的杆件时,计算杆件的失稳临界力应注意折减;必要时,应进行专项分析。
[1]中国建设网 http://news.cbi360.com/zt/jsj.
[2]余宗明.脚手架结构计算及安全技术[M].北京:中国建筑工业出版社,2007.
[3]JGJ 130-2011,建筑施工扣件式钢管脚手架安全技术规范[S].
[4]尚晓江,邱 峰,赵海峰,等.ANSYS结构有限元高级分析方法与范例应用[M].第2版.北京:中国水利水电出版社,2008.

