城市轨道交通网络末班车衔接方案的综合优化
徐瑞华,李 璇
(同济大学 交通运输工程学院,上海201804)
经过多年的轨道交通建设,北京、上海、广州等大城市目前已进入轨道交通网络化运营的新阶段.网络化运营条件下,原本独立运营的各线路通过换乘站产生直接或间接的联系,轨道交通客流也通过换乘站实现在不同线路上的流动.由于各线路结束运营的时刻不同,网络上各车站之间的可达关系呈现出动态变化的特点,一条线路的末班车时刻不仅影响到本线乘客的出行,更大程度上通过到达换乘站的时刻将影响扩大到整个路网,末班车时刻制订的合理与否直接关系到乘客能否到达目的地,因此,根据客流流向和流量特点,对网络末班车计划进行协调编制,实现各线路末班车在换乘站的整体合理衔接非常重要.目前,国外涉及城市轨道交通换乘衔接优化的研究[1-4]主要集中于常规公交与轨道交通列车时刻表的协调优化方面,尚无针对轨道交通系统内部各线路间的末班车衔接问题的研究,国内的研究也处于起步阶段,少数关于城轨末班车的研究[5-6]存在衔接关系确定的主观性太强、未结合换乘客流特点等问题.
在列车区间运行时分、停站时分及各换乘站的换乘走行时间均已知的前提下,协调编制城市轨道交通网络末班车计划就是根据一定的线路衔接关系逐步推算各条线路上、下行方向的末班车在换乘站的到发时刻及始发时刻,由于网络化运营条件下,网络规模大、换乘站数量多、换乘关系复杂,列车在各换乘站的衔接关系存在相互制约、相互影响,因此制订面向全网络最合理的末班车衔接计划难度很大,而关键则是需要确定基于全网络整体优化的各换乘站末班车的推算顺序及衔接关系,这里称为网络末班车衔接方案.本文通过分析确定衔接方案应考虑的因素,建立了网络末班车衔接方案优化模型,并借鉴最小生成树的Kruskal算法思想,综合考虑客流需求和运营者的特定衔接需求,提出了网络末班车衔接方案的优化算法.
1 网络末班车衔接关系分析
1.1 单个换乘站末班车衔接关系分析
两线换乘的条件下,末班车在换乘站的衔接具有以下3种情形:双方向衔接、单方向衔接和无方向衔接3种.其中,双方向衔接即两列末班车的乘客可以相互换乘,由于地铁换乘站大多设置换乘通道,换乘走行时间较长,而双方向衔接要求列车停站时间能够同时满足双向换乘的走行时间要求,实际中较难实现;单方向衔接是只有一列末班车的乘客可以换乘至另一列车,而反向无法换乘,这是最常见的一种衔接状态,也是进行末班车计划协调时重点考虑实现的状态;而无方向衔接即两列末班车的乘客无法相互换乘,此为最差衔接状态,是编制末班车计划时应尽量避免的.
多线换乘条件下,以某一个N线换乘站为例,若其中有Nt条线路通过此换乘站,Ne条线路终止于此换乘站,在不考虑同一线路上、下行方向之间的换乘的前提下,该换乘站的末班车换乘衔接关系有(2Nt+Ne)2-(4Nt+Ne)种,对该换乘站涉及的2N列末班车进行到发时刻推算,需要选择其中的2N-1个衔接关系作为推算基础,本文将它们称为“主动衔接关系”.
1.2 多个换乘站末班车衔接关系分析
对某一个由N条线路组成的城市轨道交通网络而言,路网规模越大,换乘站数量越多,末班车的换乘衔接关系越复杂,对路网中的2N列末班车进行时刻推算,需要依据的主动衔接关系为2N-1个,每个主动衔接关系都发生在某个换乘站内,将这些换乘站称为“主协调换乘站”.
由于路网中多个换乘站之间的衔接关系存在矛盾,一个换乘站内部的衔接关系之间也存在矛盾,主要表现在以下几个方面:同一个衔接关系不可能在两个换乘站同时实现;形成“回路”的衔接关系不能同时实现(如Line A上行→LineB上行,LineB上行→LineC下行,LineC下行→Line A上行);两列末班车涉及的两个衔接关系不能同时实现(如Line A上行→LineB上行和LineB上行→LineA上行).确定网络末班车衔接关系,就是需要从庞大的衔接关系集中选出彼此没有矛盾的主动衔接关系和主协调换乘站,形成一个衔接方案,这是编制网络末班车计划需要解决的关键问题.
2 网络末班车衔接方案优化模型
从城市轨道交通网络运营的基本要求来看,网络末班车衔接需要保证乘客能够到达目的地,即衔接方案优化的目标是使网络换乘站能够换乘到末班车的乘客数量最大化.同时,由于某些特殊的运营需求,运营者可能要求末班车衔接方案要实现某些特定的衔接关系,那么衔接方案优化需要将运营者对衔接关系的特定要求作为约束条件.因此,可建立如下的网络末班车衔接方案优化模型:
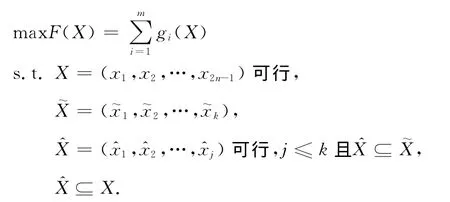
式中:X是包含2n-1个主动衔接关系的衔接方案,当这些衔接关系不存在矛盾时,称X为可行衔接方案,n为路网的线路数;m为路网的换乘站数;gi(X)是衔接方案为X时,第i个换乘站内能够换乘至末班车的乘客数量;是运营者要求实现的特定衔接关系集合,包含k个衔接关系,是的子集;同时,⊆X保证衔接方案考虑了运营者对衔接关系的特殊需求,但衔接方案中包含的特定衔接关系彼此间不能存在矛盾,因此,第三个约束条件要求可行.
路网线路数量越多,可行衔接方案数也越多,即X的可行域越大,且可行衔接方案与路网结构相关,无法用数学公式将X的可行域表达出来,则无法通过对比不同可行解的目标函数值来找出最优解,因此用传统优化方法或启发式搜索算法均很难求解.本文放弃对比寻优的求解思路,直接以优化目标为向导,来确定能够使目标函数最大化的最优衔接方案,通过分析将其转化为最大生成树问题,借鉴Kruskal算法的基本思想,提出了基于乘客换乘需求和运营者的特定衔接需求的网络末班车衔接方案优化算法.
3 网络线路衔接关系表示
3.1 线路衔接关系的赋权无向图表示法
轨道交通运营线路有上、下行的区分,为了描述这种带有方向性的线路之间的连通关系,通常将城市轨道交通网络用有向图来表示,建立车站到顶点的映射和区间到有向边的映射.本文考虑将分方向的线路抽象为顶点,用无向图G来描述城市轨道交通网络中的线路衔接关系.G为一个有序二元组,记为G=(V,E),其中,V=(v11,v12,v21,v22,…,vn1,vn2)为顶点集,表示路网中分方向的线路集合,n为网络线路的条数,vi1和vi2(i∈{1,2,…,n})分别表示某条线路i的上、下行方向;E是由V中的无序的元素偶对eip,jq=(vip,vjq)所构成的边集(i,j∈{1,2,…,n},i≠j,p,q∈{1,2}),表示路网中线路间的衔接关系集合.
对E中每一条边eip,jq赋以相应的权值ωip,jq,则G成为一个赋权无向图,ωip,jq代表eip,jq对应的衔接关系的晚间时段换乘客流量.若线路i和线路j有1个换乘交点,则vip和vjq将涉及一个“衔接关系对”,即vip→vjq和vjq→vip,分别表示由线路i的p方向换乘至线路j的q方向和由线路j的q方向换乘至线路i的p方向.由于只考虑单方向衔接状态,这两者在衔接方案中只可能满足其中一个;若线路i和线路j有m个换乘交点(m>1),则vip和vjq将涉及m个“衔接关系对”,这2m个衔接关系中,有且仅有一个能够作为主动衔接关系,成为vip和vjq的末班车时刻推算基础.根据第2节建立的目标函数,在图G中,对∀vip,vjq∈V,可选取两者涉及的所有衔接关系对应的换乘客流量最大的一个作为连接两者的边的权值.
经过以上分析,最终得到的赋权无向图G具有以下性质:
(1)若路网中线路有n条,则顶点集V的元素个数为2n;
(2)若路网中线路两两相交有k个交点,则边集E的元素个数为4k.这里的交点不是物理意义上的两线换乘点,仅表示两条线路可以直接换乘.
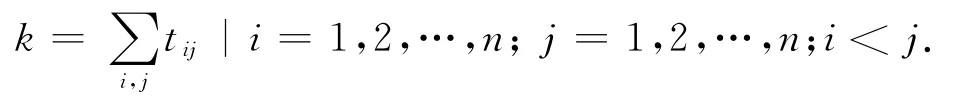
(4)由于轨道交通路网中的任意两条线路通过一次或多次换乘可达,所以图G为连通图.
在将路网表示为图G的基础上,要确定一个覆盖全网所有线路方向且没有矛盾的衔接方案,可以转化为以下问题:在图G中,寻找由某顶点vip出发,至图中所有其他顶点都恰有一条初等链的生成树T*,T*的权需满足W(T*)=max{W(T)|T为G的一棵生成树},树T*可表达为以顶点vip为根的根树,即求连通赋权无向图的最大生成树的问题.
3.2 赋权无向图表示实例
图1为一城市轨道交通路网图例,它包含4条线路{L1,L2,L3,L4},其中,L4为环线,图中箭头表示线路的下行方向;包含6个换乘站{a,b,c,d,e,g}.表1为图1所示路网晚间时段的分线路分方向的换乘客流量表,第一行和第一列中的Li上/下表示线路i的上/下行方向,行与列相交处的单元格由所在行Li上/下换乘到所在列Lj上/下的客流量及所在的换乘站序号组成,这里对客流量取了较小的数字来说明方法.图2为基于表1给出的图1所示路网的线路衔接关系的赋权无向图.

图1 城市轨道交通路网图示Fig.1 An urban rail transit networ k

图2 图1路网的赋权无向图Fig.2 Undirected edge-weighted graph of Fig.1
3.3 线路衔接关系的矩阵表示法
上例中,路网的线路条数n=4,线路两两相交的交点数k=6,其对应的赋权有向图中的顶点数为8,弧数为24.而实际的城市轨道交通路网线路数更多,线路之间的关系更为复杂,对应的赋权无向图中的元素数量将更大,下面考虑用矩阵的形式来表示赋权无向图包含的顶点与顶点及顶点与边的关联关系.
构造一个2n×2n矩阵(n为路网线路数)B=(bip,jq)2n×2n,行标号和列标号对应图G中的顶点下标(i,j∈{1,2,…,n},i≠j;p,q∈{1,2}),其中,

表1 图1路网的换乘客流量表Tab.1 The volume of transfer passenger flow of Fig.1
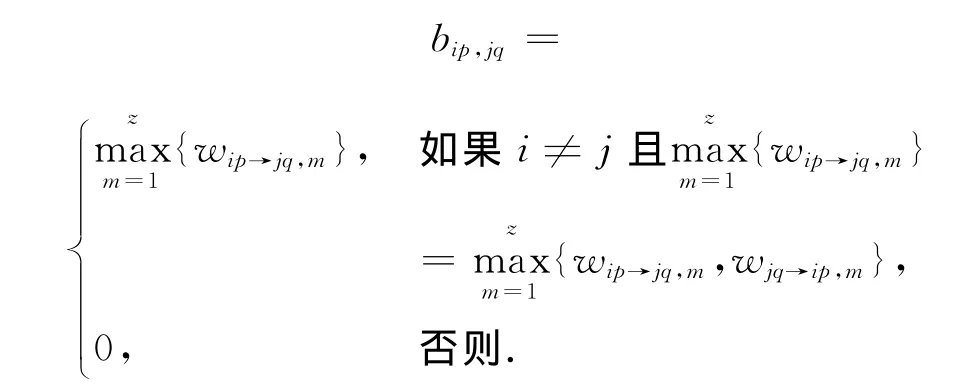
与上文相同,wip→jq,m仍表示在换乘站m由线路i的p方向换乘至线路j的q方向的客流量.B中不为零的元素个数与图G中边集E的元素个数相同,为4k(k的意义同上).在矩阵B外的左边一列及上方一行标出了图G的诸顶点(全文同),分别表示衔接关系中的起线方向和到线方向,如下侧矩阵所示.
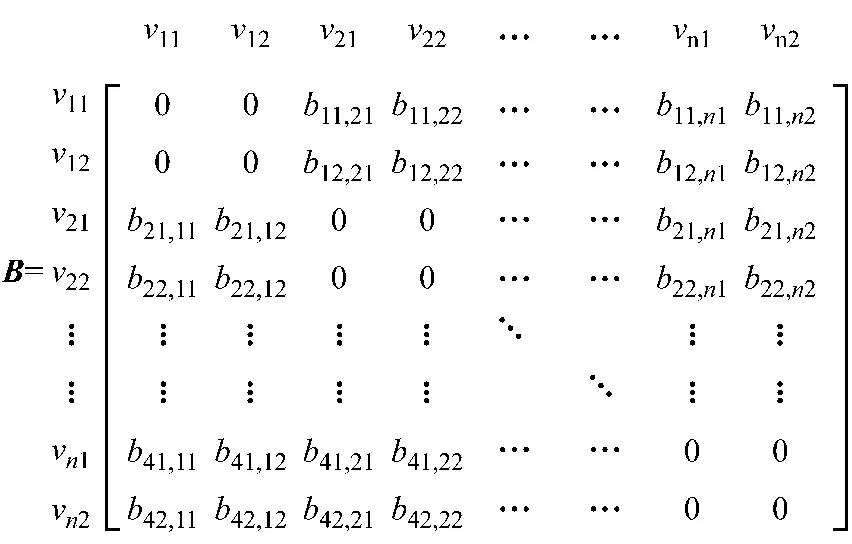
图1所示路网对应的矩阵如下侧矩阵所示.以L1上行和L2上行这一对线路为例,它们涉及2个衔接关系,L1上行→L2上行和L2上行→L1上行,对照表1可知,前者在换乘站a的换乘客流量为23,后者在换乘站a的换乘客流量为66,两者中较大者为66,根据对线路衔接关系矩阵的定义,b11,21=0且b21,11=66.其他矩阵元素的确定方法同上,由于换乘站与换乘客流量一一对应,线路衔接关系的矩阵表达间接包含了线路衔接所在的换乘站的信息.

4 网络末班车衔接方案优化算法
求最小生成树的Kruskal算法是在给定图的基础上,根据边的权值依次找出权值最小的边加入生成树,直至生成树包含原图中的所有节点,即形成最小生成树,规定每次添加的边不能造成生成树有回路[7].该算法的思路和流程同样适用于求最大生成树,如前所述,网络末班车衔接方案优化问题可以转化为求连通赋权无向图的最大生成树的问题,因此,本文借鉴Kruskal算法的基本思想,基于线路衔接关系的矩阵表示,设计网络末班车衔接方案优化算法.
4.1 考虑乘客换乘需求的基本算法
根据“在无回路的条件下优先选取较大的元素”这一原则,从矩阵B中逐个挑选出2n-1个元素,依次添加到主动衔接关系集合E中,算法步骤如下:
(1)取E=∅,E中元素个数记为card(E)=0;
(3)在矩阵B未标记过的元素中寻找当前最大元素,该元素须满足行标或列标对应的顶点已标记,且为了避免形成回路,该元素的行标和列标对应的顶点不能同时已标记,即,找出后将该元素进行标 记,并 添 加 到 集 合E中,,card(E)+=1.并将其行标和列标对应的顶点中未标记的2个进行标记;
(4)判断是否所有的顶点都已标记且card(E)=2n-1,若是,则算法终止,得到最优的主动衔接关系集合E*.由运营单位指定末班车时刻推算的起始线路方向,即可以该线路方向为树根,根据集合E*,对照线路衔接关系矩阵,绘制出各线路方向末班车时刻的推算关系图T*(如图3所示).T*是一个无圈连通图,即为树,并且T*是无向图,其各条边上的箭头仅表示边关联的两个顶点所代表的线路方向间的换乘衔接关系.若否,则转步骤(3).
4.2 满足特定衔接需求的改进算法
在实际运营中,运营者可能对末班车的衔接关系有某些特定的要求,如大型活动举办期间,城市轨道交通作为大容量的公共交通工具,将承担最主要的客流集散任务,为了做好散场客流的运输,保证乘客可以从直接服务于大型活动的线路换乘至其他线路到达目的地,运营者将结合活动结束时间及散场客流特点指定一些必须成立的末班车衔接关系,此时就要在满足这些特定衔接需求的基础上进行网络末班车衔接关系优化,下面给出具体的改进算法.
运营者指定多个换乘站的多个衔接关系必须实现,它们构成基准衔接关系集R,记R中包含的带方向别的线路集为V基准(V基准∈V),线路条数记为s,将推算算法分为三大步骤进行:
第一步,确定属于V基准的线路推算关系.首先,用3.1节所述方法将R中衔接关系表示为一个有向图D基准,判断D基准是否为连通图.
若D基准为连通图,则按照以下步骤进行:(1)构造基准衔接关系矩阵,记为B基准=(bip,jq)s×s,构造方法与线路衔接关系矩阵B相同,但只需将R中包含的衔接关系对应的换乘客流量表示在B基准中的相应元素位置,其余位置元素都为0,若R中针对一对带方向别的线路存在多于1个的衔接关系(协调换乘站不同或衔接方向不同),则取其中换乘客流量最大的一个填入矩阵中的相应位置;(2)以B基准为基础,按照3.1节所述推算步骤,可得到基准主动衔接关系集E基准.
若D基准为分离图,则可将D基准分为若干个连通子图(连通子图的数目记为h),对每个连通子图,分别按照上述连通图的步骤进行推算.对于只包含两个节点的连通子图,无需推算,其对应的基准主动衔接关系子集只包含一个元素,即图中唯一弧的权值.最终,可得到h个基准主动衔接关系子集,E基准=E基准1∪E基准2∪…∪E基准h.
第二步,确定全路网分方向线路的推算关系.首先,构造全路网线路衔接关系矩阵B.
若D基准为连通图,则将不属于V基准的线路与路网其他线路的衔接关系在B中表示出来,接着按照以下 步 骤 进 行:(1)取E=E基准,card(E)=card(E基准),将属于V基准的顶点在矩阵B外进行标记;(2)在B未标记过的元素中寻找最大元素,该元素须满足行标或列标对应的顶点已标记,且不能同时 已 标 记,且找出后将该元素进行标记,并添加到集合E中,+=1,并将其行标和列标对应的顶点中未标记的2个进行标记;(3)判断是否所有的顶点都已标记,若是,则算法终止.若否,则转步骤(2).
若D基准为分离图,则在矩阵B中,表示出不属于V基准的线路与路网其他线路的衔接关系,及分属于不同连通子图的线路间的衔接关系,接着按照以下 步 骤 进 行:(1)取E=E基准1,card(E)=card(E基准1),将属于V基准1的顶点在矩阵B外进行标记;(2)在B未标记过的元素中寻找最大元素,该元素须满足行标或列标对应的顶点已标记,且不能同时已标记,找出后将该元素进行标记,并添加到集合E中,E=E∪{ip,jq},card(E)+=1,并将其行标和列标对应的顶点中未标记的2个进行标记,若这2个顶点属于D基准的某个连通子图,则将该连通子图对应的E基准i|i∈{2,3,…,h}添加到E中,E=E∪E基准i,card(E)+=card(E基准i),同时,将属于V基准i的顶点在矩阵B外进行标记;(3)判断是否所有的顶点都已标记,若是,则算法终止.若否,则转步骤(2).
第三步,根据最终得到的主动衔接关系集合E*,绘制路网末班车时刻的推算关系图T*.
5 算例
以2.2节中路网为例,结合对矩阵元素和顶点的标记过程(以“□”作标记),来说明基本算法的步骤:a—b—c—d—e—f—g.
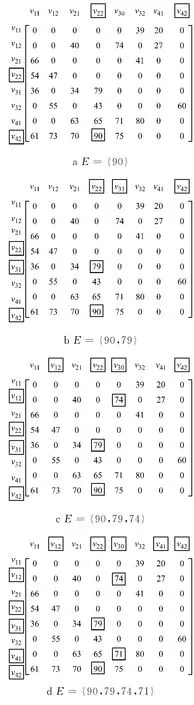

设L4下行方向为起始线路方向,那么根据E*和线路衔接关系矩阵,可得到以v42为树根的路网末班车时刻推算关系图T*,如图3a所示.由于换乘客流量数值彼此不同,线路衔接关系与换乘客流量是一一对应的,所以根据E*和T*,对照换乘客流量表,可得到表2所示的路网末班车时刻推算关系表.
若运营者指定衔接关系{换乘站d的L4上行→L3下行,换乘站a的L3下行→L1下行}必须成立,那么利用改进算法可得到主动衔接关系集E′*=,及图3b所示的最优生成树T′*.

图3 路网末班车时刻的推算关系图Fig.3 The calculation relationship graph of the last trains in urban mass transit network

表2 路网各线路方向的末班车时刻推算关系表Tab.2 The calculation relationship Table of all the last trains in urban mass transit network
6 结语
为了提高网络化运营条件下城市轨道交通客运服务水平,运营管理部门应在准确把握路网客流特点的基础上,协调优化网络末班车计划,促成各线末班车在换乘站的合理衔接.本文基于乘客的换乘需求及运营者的特定衔接需求,提出了网络末班车衔接方案优化模型和算法,通过该算法可最终得到以某个指定起始线路方向为基础的网络末班车时刻推算关系表,基于该推算关系表,设定起始线路方向的末班车始发时刻,依据列车区间运行时分、停站时分、换乘衔接时间,可逐步推算其余各线路方向的末班车在主协调换乘站的到发时刻,既而计算出末班车的始发时刻及在所有车站的到发时刻,则最终得到基于网络整体优化的末班车衔接时刻表.本算法的适用性强,可以辅助城市轨道交通网络的末班车计划编制.
[1] Younan B J.Improving transit service connectivity:the application of operations planning and operations control strategies [D]. Cambridge: Department of Civil and Environmental Engineering of Massachusetts Institute of Technology,2004.
[2] Lee K T.Optimization of timed transfers in transit terminals[D].College Park:University of Maryland,1993.
[3] Ting C J.Transfer coordination in transit network[D].College Park:University of Maryland,1997.
[4] Chung E H.Transfer coordination model and real-time strategy for inter-modal transit services[D].Toronto:Department of Civil Engineering of University of Toronto,2009.
[5] 徐瑞华,张铭,江志彬.基于线网运营协调的城市轨道交通首末班列车发车时间域研究[J].铁道学报,2008,30(2):7.XU Ruihua,ZHANG Ming,JIANG Zhibin.Study on departure time domain of the first and last trains of urban mass transit network based on operation coordination [J].Journal of the China Railway Society,2008,30(2):7.
[6] 罗钦,徐瑞华,江志彬,等.基于运行图的轨道交通网络动态可达性研究[J].同济大学学报:自然科学版,2010,38(1):72.LUO Qin,XU Ruihua,JIANG Zhibin,et al. Dynamic accessibility of urban mass transit network based on train diagram[J].Journal of Tongji University:Natural Science,2010,38(1):72.
[7] 龚劬.图论与网络最优化算法[M].重庆:重庆大学出版社,2009.GONG Xun.Graph theory and network optimization algorithm[M].Chongqing:Chongqing University Press,2009.

