基于啮合特性的人字齿轮动力学建模与分析

王成，高常青，崔焕勇

(济南大学 机械工程学院，山东 济南，250022)

与斜齿轮相比，人字齿轮传动具有轴承负荷小等优点[1]，被大量使用在舰船等大功率动力驱动系统中。船舶噪声的来源之一是齿轮箱的噪声，而齿轮箱的噪声主要是由齿轮相互啮合产生的。因此，人字齿轮的设计成为船舶降噪的关键技术之一。而建立人字齿轮动力学模型，计算激励下的动态响应是人字齿轮动态设计的前提条件。对于齿轮系统振动特性的研究一直为国内、外学者所关注，并获得了大量的成果[2-5]，但就人字齿轮动力学而言还缺乏深入的研究。吴新跃等[6]虽然建立了人字齿轮动力学模型，但所建模型未全面考虑左右端斜齿轮副之间的相互影响，且没有考虑啮合冲击激励。舰船传动装置中的人字齿轮处于高速重载的传动状态，其啮合受到加工和安装误差的影响。借助轮齿接触分析技术(TCA)和承载接触分析技术(LTCA)可准确获得人字齿轮在拟真实工况条件下的啮合特性。而利用啮合接触分析的结果，可准确计算得到内部激励。因此，本文作者利用人字齿轮啮合特性的研究结果[7]，建立人字齿轮12自由度弯曲—扭转—轴向变形耦合的三维空间动力学模型，并对系统的振动响应进行了求解与分析。

1 人字齿轮系统内部激励的计算

齿轮系统的振动噪声根源于齿轮系统的动态激励，这里仅研究人字齿轮啮合时的内部激励，包括时变刚度激励、制造安装误差和轴向位移引起的误差激励以及啮入冲击激励。

利用人字齿轮副啮合接触分析的结果，可准确进行内部激励的计算，其计算流程见图 1。相关齿轮几何接触分析和承载接触分析以及人字齿轮副啮合接触分析见文献[7-10]。

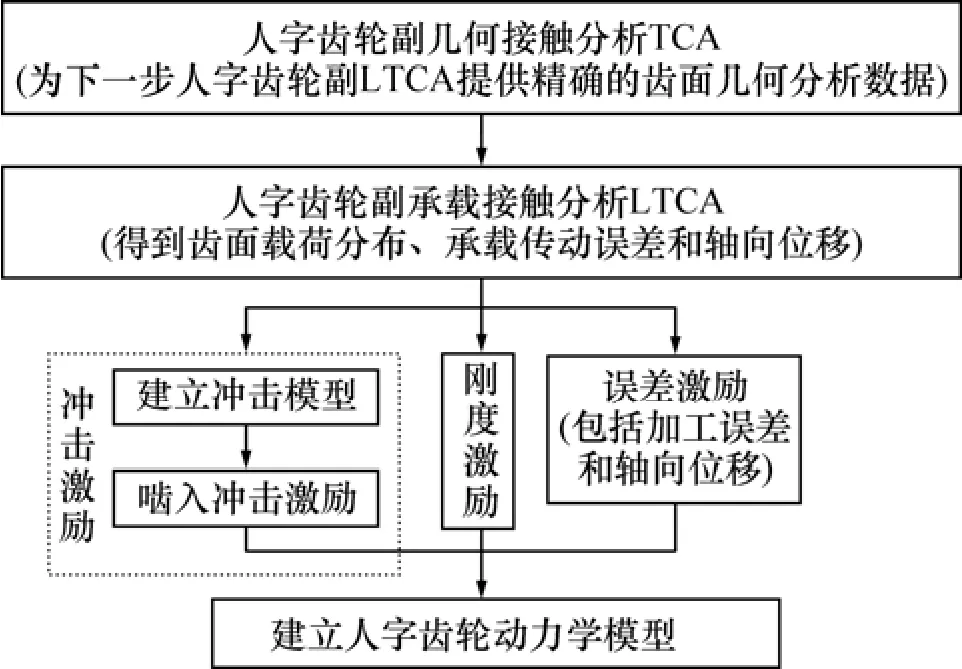
图1 内部激励计算流程图Fig.1 Flow diagram for calculation of internal excitation

1.1 人字齿轮时变刚度激励的计算

时变刚度激励源于齿轮啮合过程中啮合齿对数的变化导致轮齿啮合综合刚度的时变性而产生的动态激励[11]。

利用人字齿轮副承载接触分析得到不同啮合位置的接触力和接触变形，从而得到该位置的啮合刚度，将啮合刚度的离散值通过多项式拟合和 Fourier级数变换展开成周期函数。图2所示为某人字齿轮副1个啮合周期内的啮合综合刚度曲线图(i表示同时参与啮合的齿对数；横坐标为小轮转角，可根据小轮实际转速转化为相应的啮合时间)。在轮齿啮合过程中，若某啮合位置有多对齿同时啮合，那么该啮合位置的轮齿啮合综合刚度是由在该位置同时参与啮合的单对轮齿啮合刚度叠加而成。因此，通过反变换，求出的单对轮齿从啮入到啮出的刚度曲线见图3。

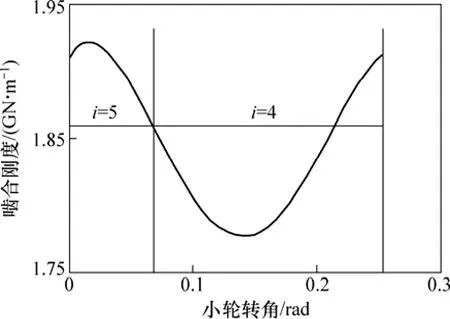
图2 人字齿轮啮合综合刚度曲线Fig.2 Meshing synthetic stiffness curve of double helical gears

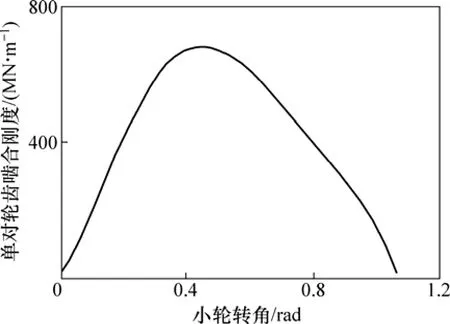
图3 单对轮齿啮合刚度曲线Fig.3 Meshing stiffness curve of single-pair teeth

1.2 人字齿轮误差激励的计算

轮齿啮合误差是由轮齿制造安装误差引起的实际齿廓与理论齿廓的偏移，目前研究中一般仅考虑齿形误差和基节误差，根据齿轮加工精度等级通过查齿轮手册然后合成系统等效误差，最后通过简谐函数来模拟误差[11]。

此外，在低转速下由于人字齿轮制造安装误差引起的轴向位移也是人字齿轮高速运动时振动的激励源。因此，根据齿形误差和基节误差，利用人字齿轮副承载接触分析得到低转速下长周期内的轴向位移[7]，经Fourier级数展开后其周期函数曲线见图4。

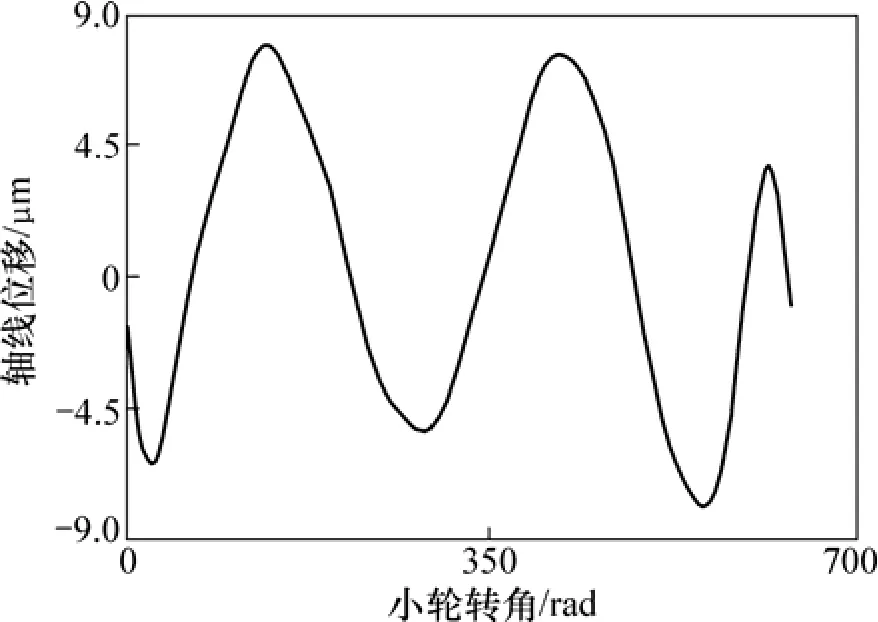
图4 轴向位移曲线Fig.4 Curve of axial displacement

1.3 人字齿轮啮合冲击激励的计算

啮合冲击主要是由啮入、啮出和节点冲击组成，三者对于齿轮传动性能的影响，节点冲击最小，啮出冲击次之，啮入冲击最大[12]。这里仅计算啮入冲击激励。

文献[12]给出了线外啮入点到正常啮入点间任意位置冲击力的计算方法。同样，将得到的啮合点的冲击力通过多项式拟合以及 Fourier级数变换展开成周期函数。某转速下一个啮合周期内人字齿轮的啮入冲击力曲线见图5。

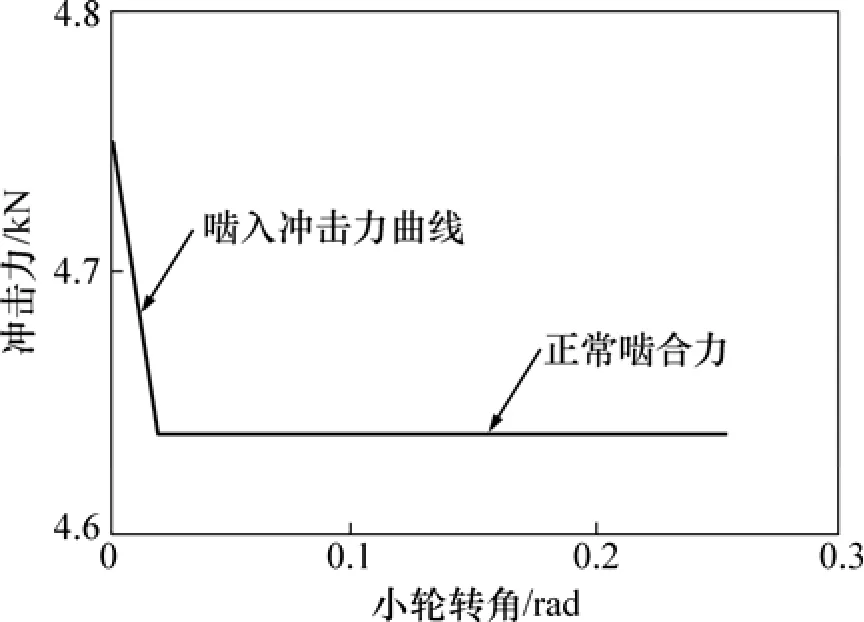
图5 人字齿轮副的啮入冲击力曲线Fig.5 Curve of corner contact impact force for double helical gears

2 人字齿轮三维空间动力学模型的建立

人字齿轮为实现均载传动，通常小轮采用轴向浮动安装。应用集中参数法建立人字齿轮弯-扭-轴耦合的三维空间动力学模型(如图6所示，图中轴的扭转刚度、阻尼与弯曲刚度、阻尼没有画出)，忽略接触齿面的摩擦，人字齿轮动力学模型是 12自由度的振动系统，这12个自由度可表示为：

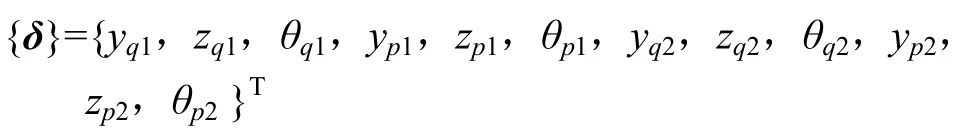
式中：yq1和zq1分别为主动轮左端的两斜齿轮中心点Oq1在y向和z向的平移振动位移；θq1为Oq1的转角振动位移；yp1和zp1分别为从动轮左端的两斜齿轮中心点Op1在y向和z向的平移振动位移；θp1为Op1的转角振动位移；yq2和zq2分别为主动轮右端的两斜齿轮中心点Oq2在y向和z向的平移振动位移；θq2为Oq2的转角振动位移；yp2和zp2分别为从动轮右端的两斜齿轮中心点Op2在y向和z向的平移振动位移，θp2为Op2的转角振动位移。

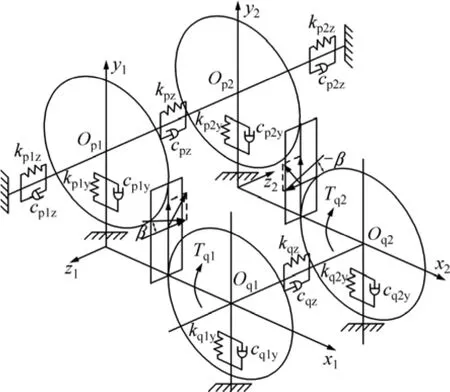
图6 人字齿轮传动的动力学模型Fig.6 Model of dynamics analysis for double helical gears

由图6可知：q1，p1和q2，p2点的振动位移与主、从动轮广义位移间的关系分别为：

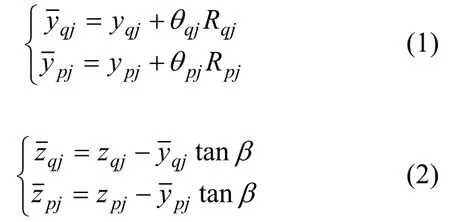
式中，j=1,2。

法向阻尼采用如下方法得到：

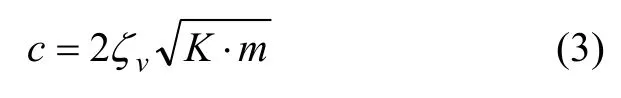
式中：m为人字齿轮副的等效质量；ζv为人字齿轮副的相对啮合阻尼系数, 这里取ζv=0.070；K为人字齿轮副的平均啮合刚度。

相应的切向和轴向刚度、阻尼和啮合误差的计算请参照文献[13]。

考虑左右端斜齿轮副之间的相互作用，切向动态啮合力可表示为：

轴向动态啮合力可表示为：

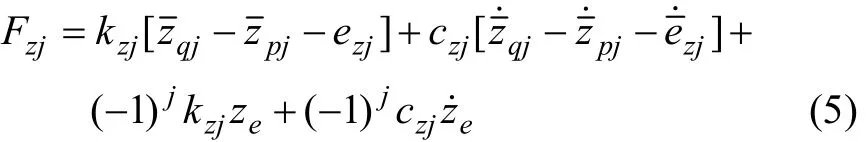
式中：i=q，p；j=1，2；kyj和kzj分别为左右端斜齿轮副切向和轴向的啮合刚度；cyj和czj分别为左右端斜齿轮副切向和轴向的阻尼；eyj和ezj分别为切向和轴向啮合误差；kqx和kpx分别为小齿轮轴和大齿轮轴的扭转刚度；cqx和cpx分别为小齿轮轴和大齿轮轴的阻尼；ze为通过人字齿轮承载接触分析得到的低转速下的轴向位移。当i=q,j=1或i=p,j=2时，s=1,否则s=2。

利用牛顿第二定律，根据图6中人字齿轮传动的动力学模型，建立人字齿轮系统的振动方程，即

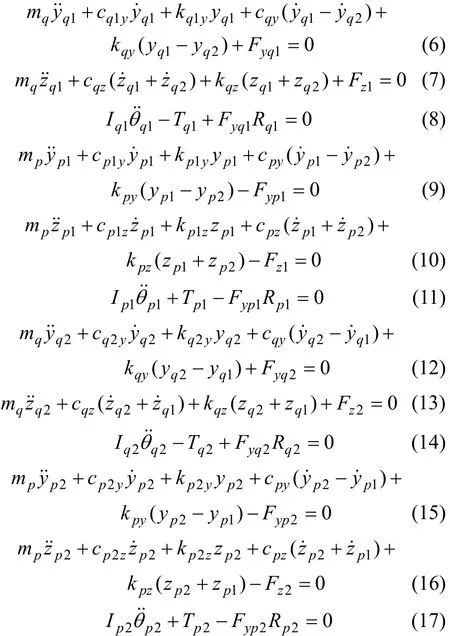
式中：k1和k2分别为左端和右端齿轮副的扭转刚度；c1和c2分别为左端和右端齿轮副的阻尼；kqy和kpy分别为小轮轴和大轮轴的弯曲刚度；cqy和cpy分别为小轮轴和大轮轴的阻尼；kqz和kpz分别为小轮轴和大轮轴的拉伸(压缩)刚度；cqz和cpz分别为小轮轴和大轮轴的阻尼。这里需要指出，啮合冲击激励被放在Tij中。

在啮合线方向上两齿面啮合点间的相对位移λi(i=1，2)可表示为：

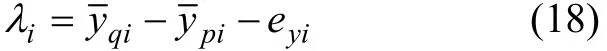
左右端轮齿扭转角相对差γj(j=q，p)可表示为：

分别将λi和γj作为新的自由度，对式中的相应方程进行合并，并将切向动态啮合力和轴向动态啮合力代入式(6)～(17)。同时，定义量纲一时间t=τwn，给定一个位移标称尺度bc，将上述方程进行量纲归一化处理[14]。

3 人字齿轮动力学模型的求解与分析

采用变步长四阶 Runge-Kutta对振动方程进行求解，考虑初始值的影响，将开始数百个周期的响应略去，计算得到位移、速度和加速度的振动时域响应，通过傅里叶变换(FFT)得到相应的频域响应。

利用上述分析方法计算 1对人字齿轮的动态特性，该对人字齿轮的参数见表1。采用表1中的参数，利用人字齿轮啮合特性的结果得到人字齿轮轮齿啮合综合刚度、单对轮齿啮合刚度和低转速下长周期内的轴向位移，根据冲击模型，计算得到人字齿轮啮入冲击激励(分别如图2～5所示)。

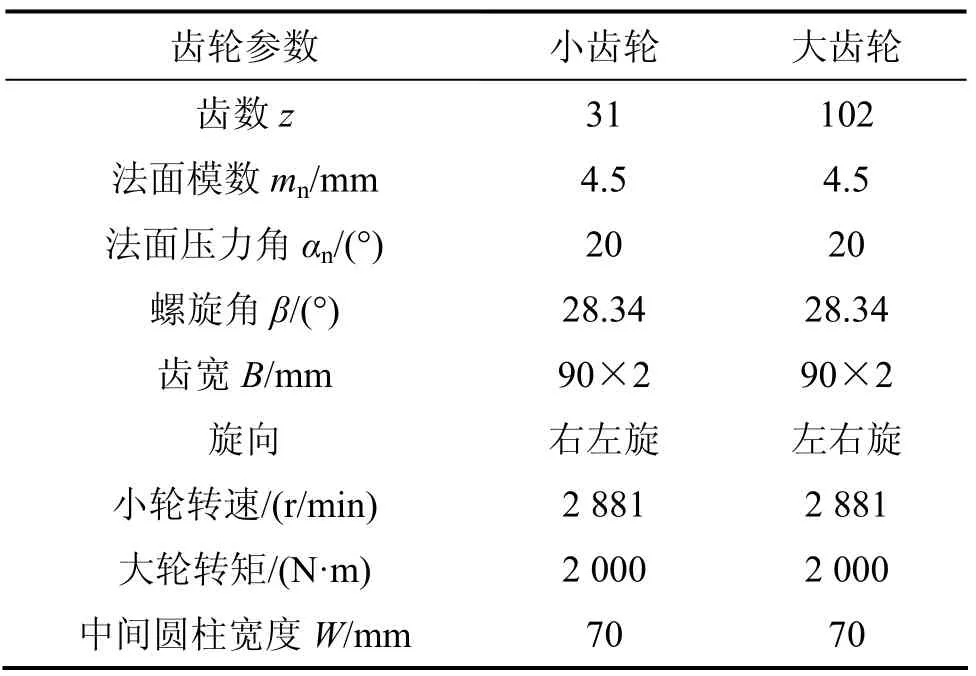
表1 人字齿轮传动的参数Table 1 Parameters of double helical gears

以左端齿轮副为例，图7所示为左端小齿轮副啮合线上相对振动加速度响应、轴向振动加速度响应和横向振动加速度响应。图8所示为与之对应的频域图。从图7和图8可看出：在该例中，扭转振动和轴向振动比横向弯曲振动大的多，因此，人字齿轮的振动噪声主要来源于前两者。对轴向振动起作用的主要是齿频激励，轴频激励频率过低(在2 881 r/min时约为48 Hz)，基本不影响系统的振动。

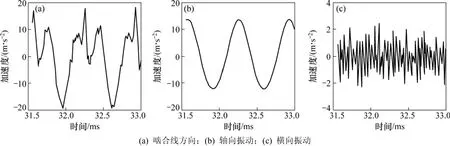
图7 时域谱Fig.7 Time-domain spectrum

图8 频域谱Fig.8 Frequency spectrum

4 结论

(1)通过人字齿轮副承载接触分析得到轮齿时变啮合刚度以及单对轮齿啮合刚度和轴向位移，根据啮合冲击计算模型，得到啮入冲击激励。

(2)应用集中参数理论建立人字齿轮12自由度的三维空间动力学模型，利用牛顿力学定律，建立人字齿轮系统的振动方程，对方程进行消除刚体位移和量纲归一化处理。

(3)采用变步长四阶龙格—库塔法进行求解，以一对人字齿轮为例，得到系统的振动加速度响应。

(4)人字齿轮动力学模型的建立、求解和分析为人字齿轮的动态设计提供了理论依据，进而为船舶降噪提供技术支持。

[1]Amendola J B. Single vs double helical gears[J].Turbomachinery International. 2006, 47(5): 34-38.

[2]Kim W, Yoo H H, Chung J T. Dynamic analysis for a pair of spur gears with translational motion due to bearing deformation[J].Journal of Sound and Vibration, 2010, 329(21): 4409-4421.

[3]Osman T, Velex P H. Static and dynamic simulations of mild abrasive wear in wide-faced solid spur and helical gears[J].Mechanism and Machine Theory, 2010, 45(6): 911-924.

[4]Ambarisha V K, Parker R G. Nonlinear dynamics of planetary gears using analytical and finite element models[J]. Journal of Sound and Vibration, 2007, 302: 577-595.

[5]Kiracofe D R, Parker R G. Structured vibration modes of general compound planetary gear systems[J]. ASME, Journal of Vibration and Acoustics, 2007, 129(2): 1-16.

[6]吴新跃, 朱石坚. 人字齿轮传动的振动理论分析模型[J]. 海军工程大学学报, 2001, 13(5): 13-19.WU Xin-yue, ZHU Shi-jian. Theoretical vibration pattern of herringbone gearing[J]. Journal of Naval University of Engineering, 2001, 13(5): 13-19.

[7]王成, 方宗德, 贾海涛. 人字齿轮均载特性的理论分析与试验研究[J]. 兵工学报, 2011, 32(1): 45-48.WANG Cheng, FANG Zong-de, JIA Hai-tao. Theoretical calculation and experimental study of load sharing for double helical gears[J]. Acta Armamentarii, 2011, 32(1): 45-48.

[8]Faydor L. Litvin, Alfonso Fuentes. Gear Geometry and Applied Theory, second edition[M]. New York: Cambridge University Press, 2004: 241-266.

[9]LI Shu-ting. Gear contact model and loaded tooth contact analysis of a three-dimensional, thin-rimmed gear[J]. Journal of Mechanical Design, 2002, 124(3): 511-517.

[10]Litvin F L. Design simulation of meshing, and contact stress for an improved worm gear drive[J]. Mechanism and Machine Theory, 2007, 42: 940-959.

[11]林腾蛟, 蒋仁科, 李润方, 等. 船用齿轮箱动态响应及抗冲击性能数值仿真[J]. 振动与冲击, 2007, 26(12): 15-22.LIN Teng-jiao, JIANG Ren-ke, LI Run-fang, et al. Numerical simulation of dynamic response and shock resistance of marine gearbox[J]. Chinese Journal of Mechanical Engineering, 2008,44(7): 52-57.

[12]周长江, 唐进元, 钟志华. 齿轮传动的线外啮合与冲击摩擦[J].机械工程学报, 2008, 44(3): 75-81.ZHOU Chang-jiang, TANG Jin-yuan, ZHONG Zhi-hua. Corner contact and impact friction of gear drive[J]. Chinese Journal of Mechanical Engineering, 2008, 44(3): 75-81.

[13]李润方, 王建军. 齿轮系统动力学[M]. 北京: 科学出版社,1997: 154-188.LI Run-fang, WANG Jian-jun. Dynamics of gear system[M].Beijing: Science Press, 1997: 154-188.

[14]杨振, 王三民, 范叶森. 转矩分流式齿轮传动系统的非线性动力学特性[J]. 机械工程学报, 2008, 44(7): 52-57.YAN Zhen, WANG San-min, FAN Ye-sen. Nonlinear dynamics characteristics of split-torque gear transmission system[J].Chinese Journal of Mechanical Engineering, 2008, 44(7): 52-57.