仿生射流表面减阻特性实验研究
赵刚,谷云庆,许国玉,夏冬来,赵华琳,姚建均
(哈尔滨工程大学 机电工程学院,黑龙江 哈尔滨,150001)
从20世纪70年代开始,降低阻力节约能源一直是国内外学者致力研究的重点问题。减阻技术不仅具有非常重要的军事价值,而且在交通运输、油气输送、体育等诸多领域都有广阔的应用前景[1]。在动力和能源一定的条件下,根据理论推算,假设将船舶表面阻力减小 10%,其航行速度和航程可以同时增加约3.57%,即使只能获得较小的减阻效果,每年也可以节约大量的能源,这对于缓解当前国内外能源危机极为重要[2-3]。生物经过亿万年不断的自适应、自学习、自重构、自繁殖而不断进化,它不仅包含机体对外界介质的即时调控,同时还包含自身经过长期进化形成的已相当稳固的对外届环境的适应性,进而形成适合其自身生存的表面外形结构[4]。在现有的减阻技术中,仿生减阻技术通过模拟生物在进化过程中获得的某些减阻特征,得到了很好的减阻效果,具有重要的工程实用价值。如采用与鲨鱼鳞片具有相似结构的沟槽表面减阻[5-9],使用与海豚表皮相似弹性特征的柔性表面减阻[10-13],利用仿照昆虫表面设计的非光滑表面减阻[14]等都是仿生减阻研究的重要成果。鱼类的鳃位于咽的两侧,直接或间接与外界相通,在胚胎的早期,外胚层也向内凹陷,内外两胚层相遇后打穿,形成鳃裂。鳃裂的数目随动物种类不同而不同,圆孔类数目多为7对鳃裂。鲨鱼终日生活在海水中,是具有快速运动能力的水生动物,在其捕食时的行进速度非常快,深海鲨鱼的爆发启动速度惊人,可达10~20 m/s。观察发现,其身侧前部排列着宽大的鳃板,每侧有5~7个鳃裂,在游动时海水通过半开的口吸入,从鳃裂流出进行气体交换,其功能除与呼吸密切相关外,还与降低自身运动阻力有关。在前期工作中,针对射流方向影响仿生射流表面减阻效果进行深入研究,得到较好减阻效果[15]。基于仿生研究的基本原理,通过对鱼类鳃裂部位的形态特征进行结构简化,建立类似鱼类鳃裂部射流特征的仿生射流表面,在实验模型表面加工出仿生射流孔结构,通过小型射流减阻测试实验平台研究仿生射流表面的减阻特性。
1 实验设备及实验模型
1.1 实验设备
仿生射流表面减阻特性实验在哈尔滨工程大学仿生减阻研究实验室完成。自行设计并制造一个评估射流减阻效果的小型射流减阻测试实验平台。该小型射流减阻测试实验平台腔体为1个充满水的封闭的循环管路,通过调速电机驱动扭矩信号耦合器带动旋转轴及负载旋转运动,并在密封仓内形成一个压力稳定的均匀流场。射流供水采用水泵供给方式,通过水泵将水槽中水泵入射流存水区,并以一定速度向密封仓内进行射流。小型射流减阻测试实验平台主要设备包括:(1)YVP系列变频调速三相异步电动机。电机功率为1.5 kW,通过型号为E1000系列变频器进行转速调控;(2)扭矩信号耦合器。扭矩信号耦合器两端轴颈通过联轴器分别与电机和旋转轴相联接,测试实验过程中流体对实验模型表面的摩擦扭矩;(3)数据采集系统。自行设计开发的数据采集系统,在 LabVIEW 环境下编写图形用户界面,实现对数据流程的软件控制,采集实验过程中不同实验模型下流体对其表面的摩擦扭矩值,达到对数据采集的自动化及数据监控的实时化;(4)水泵。射流供给动力装置。(5)联想计算机。
减阻测试实验平台结构图如图1所示。其中,密封仓为1个圆形仓体,内腔压力为常压状态,直径×高度为 180 mm×125 mm,距小端面一侧距离为 70 mm处正中顶端处和底端处分别开有直径为6 mm的通孔,便于向密封仓内注入流体及作为射流出水管孔。实验模型旋转速度范围为0~5 000 r/min,连续可调;扭矩信号耦合器量程范围为 0~10 N/m,率响应为100 μs。
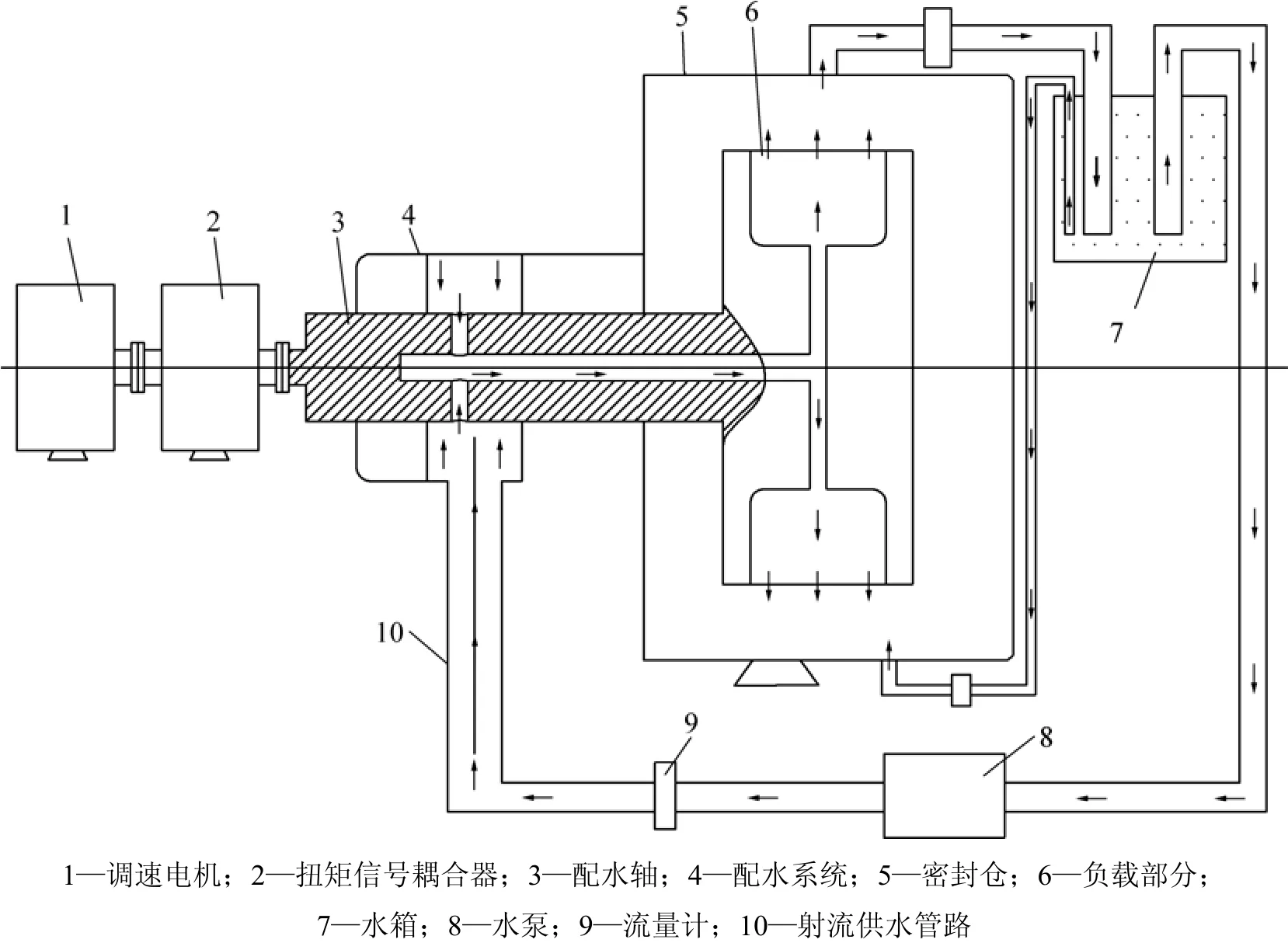
图1 小型射流减阻测试实验平台结构图Fig.1 Schematic of small jet drag reduction testing platform
实验平台电机通过联轴器带动扭矩信号耦合器运行,扭矩信号耦合器通过联轴器带动负载运行;负载主要包括射流供水部分和实验模型部分。本实验为对照实验,其中实验模型为可更换构件,实验过程中,通过扭矩信号耦合器显示出不同射流表面实验模型与对照的光滑表面模型在相同转速、相同实验环境下所受到流体摩擦扭矩,通过摩擦扭矩来量化减阻效果。电机通过变频器进行转速调节,扭矩信号耦合器将信号依次通过变送器、采集卡至计算机中,通过LabVIEW软件对数据进行读取并存储。在软件界面中可以读取系统中扭矩瞬时值和扭矩随时间变化曲线图及扭矩信号耦合器输出端转速变化瞬时值和转速随时间变化曲线图。
1.2 实验模型
考虑到密封仓尺寸、实验模型自身质量及形状对系统影响、材料成本、模型加工及产品质量,最终选择U-PVC管作为实验模型载体。分别截取直径×高度为160 mm×50 mm、壁厚为5 mm的几段圆形管路。实验模型的形位公差为7级精度,表面粗糙度为0.8。射流孔结构加工在实验模型表面上,加工成通孔,沿周向及轴向按照一定规律分布。实验模型表面射流孔加工方法如下:设计专用夹具(夹具由钻模、螺栓及专用压板等组成,实验模型通过螺栓专用压板固定在可倾式工作台上,钻模通过螺纹固定在模型上),通过与可倾式工作台配合使用,高质量地加工出射流孔;定位方式可依据不同实验模型的实际结构以及精度需要而定。射流孔具体排布方式为:在实验模型周向平均分布10个射流孔(a=36°),轴向分布 5排射流孔,每排10个,共计50个射流孔。其中轴向第1排孔、第3排孔和第5排孔相对应的每3个射流孔在同一母线上;第2排孔、第4排孔相对应的每2个射流孔在同一母线上,二者母线与实验模型圆心所成面的二面角θ=18°。第3排孔位于实验模型中间部位,与第1排孔和第5排孔之间距离均为20 mm,第2排孔与第4排孔距较近一侧端面距离均为20 mm,实验模型结构如图2所示。射流孔径D分别取1.2,2.0,3.0和4 mm 4组,共计5组实验模型,其中包括一个表面不带射流孔光滑实验模型。为避免加工过程中U-PVC管因受力不均而产生变形,加工出与U-PVC管内孔相配套的圆形衬套,当在实验模型表面加工射流口时,将圆形衬套安装在 U-PVC管内腔中,达到提高管壁强度的功效。
射流实验过程中,当一次实验完成后,只需要更换实验模型即可,而不需要进行其他部位拆卸,保证了不同实验模型情况下实验状态的一致性,也避免了实验过程中定位误差及装配误差等,并且操作容易所需时间短。实验平台工作时振动小,噪声低,水循环利用,起到环保、节约资源的功效。
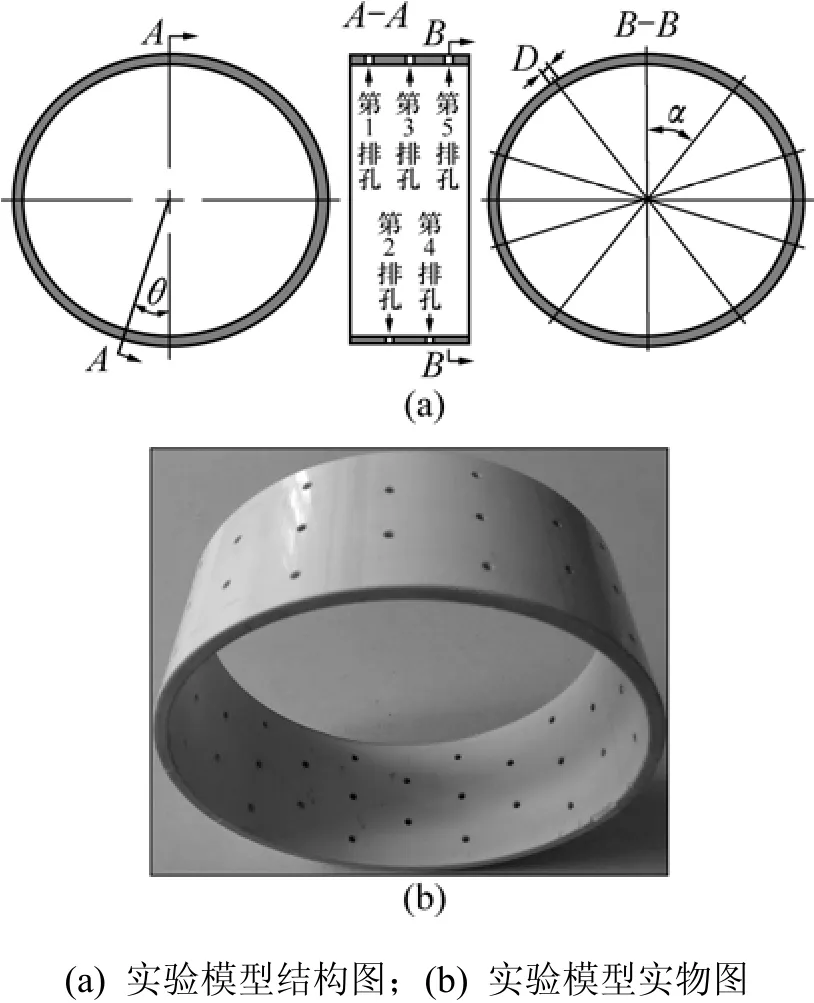
图2 射流表面实验模型结构示意图Fig.2 Structure schematic drawing of experimental model and jet surface
2 测试实验工作原理及评估方法
2.1 工作原理
在密封仓内没有注入水之前,实验平台电机未启动,实验模型表面不受摩擦阻力;启动电机,测得此情况下实验平台系统的摩擦扭矩,用于对数据采集系统采集数据进行修正,保证实验过程中所采集的扭矩即为实验模型所受到流体对其的摩擦扭矩。以上工作校验好后,停止电机运行,通过密封仓底端管路向密封仓内注入水,当顶端管路有均匀水流流出时,表明水已经注满腔体。射流供给采用水泵供给。启动电机,通过变频器调节电机转速,继而调控实验模型旋转转速,实验模型在水中旋转过程中受到水对其表面的摩擦阻力,该摩擦阻力作用于扭矩信号耦合器表现为扭转力矩,这个变形通过扭矩信号耦合器转变为频率信号,频率信号经由数据采集系统,送至计算机中,通过基于 LabVIEW 环境下编写图形用户界面,最终以扭矩的形式显示出测量值及即时变化曲线。同时,扭矩信号耦合器通过码盘采集自身输出轴的转速,将信号一并输计算机中,在数据采集用户界面显示出转速即时值及即时变化曲线。
为了避免测试系统误差,提高流体阻力测试的准确性,实验之前对测试系统进行零点标定。通过进行多次无信号输入状态测试采样之后,对零点误差进行剔除极值后取平均的方法进行统计分析,同时将处理后得到的误差值存储计算机中,在进行正式的实验测试时,实验值减去预先存储在计算机中的每次测量的零点误差后即为真实测量值,通过该方法可以有效消除测试值零点误差。
2.2 评估方法
实验中采集时间为0.05 s,为了得到稳定性较好的实验数据,剔除前500次所采集的数据,从501次起,共取300次。分别计算不同实验模型情况下的300组数据的平均值,对数据进行分析处理。
实验过程中分别对光滑表面实验模型和不同射流孔径的实验模型进行扭矩测试,旋转速度r依次取2 500,2 600,2 700,2 800,2 900,3 000,3 100,3 200,3 300,3 400,3 500和 3 600 r/min,共12组旋转速度。水温为 20 ℃。通过光滑表面实验模型与相同条件下开有不同射流孔径的实验模型的摩擦扭矩进行比对,来评估仿生射流表面的减阻效果,减阻率R计算公式为:
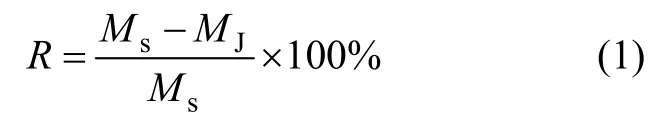
式中:Ms为光滑表面实验模型所受摩擦扭矩,N·m;MJ为射流表面实验模型所受摩擦扭矩,N·m。
旋转过程中由于水的黏性作用而对实验模型产生摩擦阻力,继而产生摩擦扭矩,其中,摩擦阻力f为
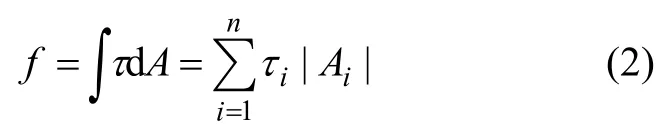
式中,τ表示壁面剪应力,MPa;A表示壁面面积,m2;τi表示壁面离散单元剪应力,MPa;Ai表示壁面离散单元面积,m2。
由式(2)可得摩擦扭矩公式:
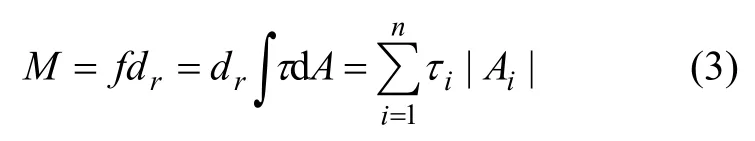
由于实验模型与回转中心间距离为定值,由式(3)可知,通过实验模型表面所受摩擦扭矩来反应减阻率与采用实验模型表面所受阻力来反应减阻率效果一致。
3 实验结果与分析
在旋转速度为2 500~3 600 r/min(间隔为100 r/min)下,依次对光滑表面、射流孔径分别为1.2,2.0,3.0和4.0 mm实验模型下,测试水对其表面的摩擦扭矩,并计算出各射流表面的减阻率,实验结果如表1所示。
图3所示为不同表面结构实验模型的摩擦扭矩特性曲线,图4所示为仿生射流表面实验模型随旋转速度变化曲线。由表1和图3可知,不同表面结构实验模型随旋转速度增大,所受摩擦扭矩变化梯度越来越大,当旋转速度增大至3 000 r/min时,光滑表面实验模型所受的摩擦扭矩明显大于射流表面实验模型所受的摩擦扭矩,其中射流孔径为3 mm的实验模型所受摩擦扭矩最小。由表1和图4可知,旋转速度为3 000 r/min以下时,射流表面出现增阻力现象,随着旋转速度不断增加,增阻现象逐渐减小;当旋转速度达到3 000 r/min时,射流表面出现减阻效果,且随着旋转速度不断增加,减阻率逐渐增大。从图4可以看出:旋转速度在3 000 r/min以上时,射流孔径为3 mm表面结构减阻效果最好、射流孔径为4 mm表面结构减阻率其次、射流孔径1.2 mm表面结构减阻效果最差;旋转速度在3 000 r/min以下时,射流孔径为2 mm表面结构增阻效果变化梯度最大,增阻最为明显;当旋转速度为 3 500 r/min、射流孔径为3 mm时,减阻率最大,为10.8%;当旋转速度为2 500 m/min、射流孔径为2 mm时,增阻效果最大,为11.7%。
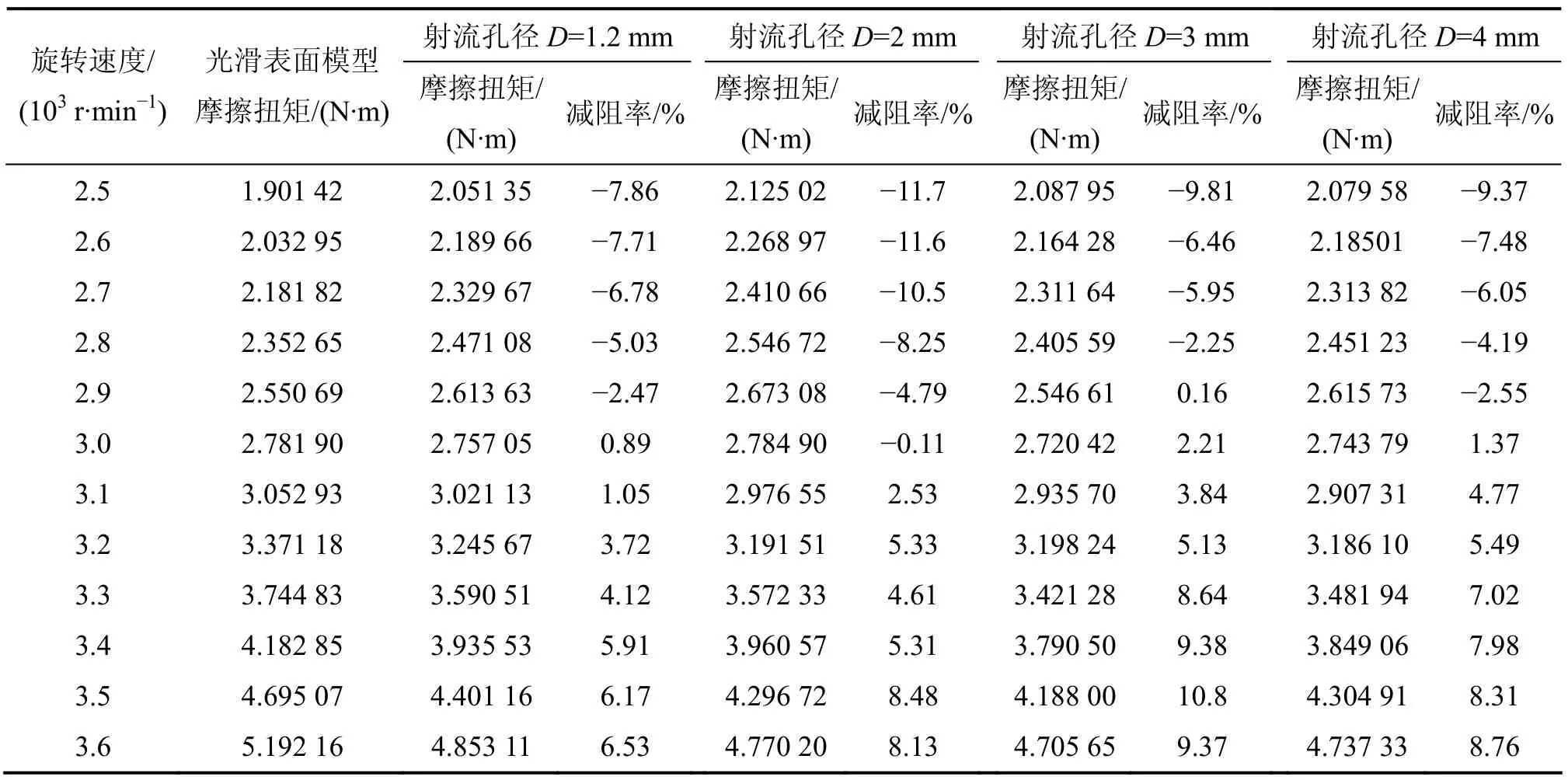
表1 不同表面结构实验模型在不同旋转速度下的实验结果Table 1 Variable rotational speed experiment result of experimental model with variable surface structure
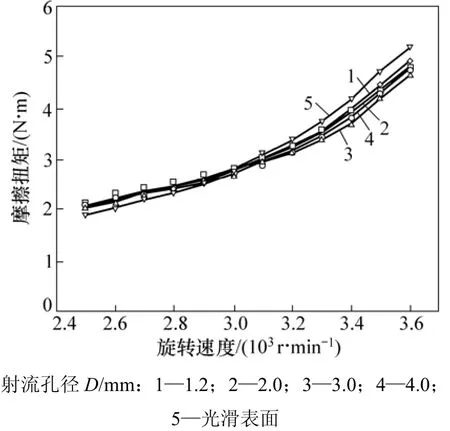
图3 实验模型摩擦扭矩随旋转速度变化特性曲线Fig.3 Friction torque characteristic curves of experimental model vs. rotational speed
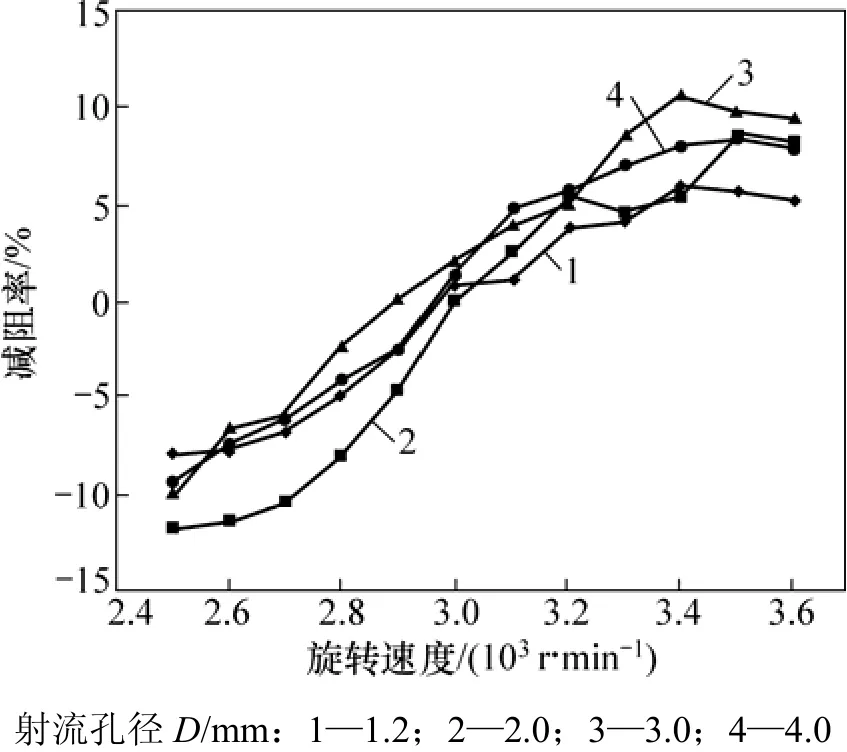
图4 仿生射流表面减阻率随旋转速度变化曲线Fig.4 Drag reduction effect curves of bionic jet surface vs. rotational speed
结合前期对仿生射流表面减阻特性仿真分析结果及本次实验结果可以认为:与模型表面无射流孔的光滑表面所受摩擦阻力相比,射流表面在一定条件下,可以明显降低射流孔沿旋转方向下游流域的摩擦阻力,这与射流过程中产生的漩涡有着密切关系。在射流过程中,射流孔下游近壁面处低速流场厚度增加,即边界层黏性底层增厚,相应速度梯度降低,使得壁面所受剪应力降低,摩擦阻力减小。当实验模型旋转速度增大时,射流速度增大,射流孔下游近壁面处出现漩涡,此时漩涡速度较低,相当于边界层黏性底层继续增厚,壁面所受剪应力降低,表现减阻状态;随着旋转速度逐渐增大,漩涡尺寸和速度逐渐增大,致使射流孔壁面附近产生反向流,反向流与漩涡同步发生变化,反向流对射流孔下游流域产生逆流向的推动作用,致使摩擦阻力下降。因此,随着射流速度逐渐增加,射流孔下游流域漩涡不断发展,影响下游减阻流域范围变大,表现出明显的减阻效果;此外,当旋转速度增加到一定程度时,由于漩涡的作用,使相邻射流孔之间的边界层的速度梯度增大,壁面切应力增大,致使摩擦阻力增加,此时,减阻率变化梯减小。
在实验模型旋转过程中,射流孔在沿旋转方向下游一侧形成漩涡,漩涡的不断发展变化致使射流孔壁面附近产生反向流,反向流速度随漩涡的发展而增大,最终对出口射流产生逆流向的推动作用,导致了摩擦阻力下降,呈现出减阻趋势。但是,漩涡运动的能量一方面来自于自身动力作用,另一方面来自外界流场的作用,近壁面处外界流场在为射流孔下游漩涡运动提供一定能量后其自身速度降低,将无法继续提供足够的能量去推动下一个漩涡运动,只有当外界流场本身获得一定能量后,才能继续完成下一次能量的传递过程,这就需要射流自身提供能量,因此,随着射流速度的增加,减阻率变大。随着旋转速度继续增加,射流表面所受到水的黏性阻力越来越大,漩涡所能提供的减阻变化梯度小于水黏性阻力所产生的增阻变化梯度,实验模型表面流场接近于光滑表面,减阻效果逐渐削弱;当漩涡所能提供的减阻变化梯度完全不能克服黏性阻力所产生的增阻变化梯度时,呈现出增阻状态。根据以上对射流减阻特性分析,可以推测:在射流孔径一定情况下,存在1个合适的旋转速度使射流表面减阻效果达到最佳;在射流孔径不同情况下,射流过程中所形成漩涡大小、结构、速度、运动状态等特性不尽相同;同时,射流孔排布、射流速度等均对射流过程中形成漩涡有影响作用。因此,射流孔径、射流孔排布、外界流场速度、射流速度等相关因素都直接影响着射流表面的减阻特性。
4 结论
(1)仿生射流表面能够改变水对其表面的摩擦阻力,具有一定的减阻效果,减阻率与实验模型转速、射流孔径、射流速度密切相关。
(2)当射流孔径一定、旋转速度在3 000 r/min以上时,减阻率随着实验模型旋转速度的增而增加,最大减阻率为10.8%。
(3)实验模型表面分布垂直射流孔具有较好的减阻效果,下一步需要探索非垂直射流孔情况下射流减阻特性,射流孔排布、射流孔不同形状对减阻效果的影响,以及射流各相关因素之间相互耦合情况对射流表面减阻特性的影响。
[1]李新华, 董守平, 赵志勇. 平板及减阻沟槽表面雷诺应力的实验研究[J]. 实验流体力学, 2006, 20(1): 40-44.LI Xin-hua, DONG Shou-ping, ZHAO Zhi-yong. Experimental study on Reynolds shear stress in turbulent boundary layers over smooth and drag reduction grooved surface[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(1): 40-44.
[2]Koeltzsch K, Dinkelacker A, Grundmann R. Flow over convergent and divergent wall riblets[J]. Experiments in Fluids,2002, 33(2): 346-350.
[3]黄桥高, 潘光, 胡海豹, 等. 脊状表面航行器模型减阻特性的水洞实验研究[J]. 实验流体力学, 2010, 24(3): 50-53.HUANG Qiao-gao, PAN Guang, HU Hai-bao, et al.Investigation about drag reduction characteristic of riblets surface on vehicle model in water tunnel[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(3): 50-53.
[4]张成春, 任露泉, 刘庆平, 等. 旋成体仿生凹坑表面减阻试验研究[J]. 空气动力学学报, 2008, 26(1): 79-84.ZHANG Cheng-chun, REN Lu-quan, LIU Qing-ping, et al.Experimental study on bionic dimpled surfaces of bodies of revolution for drag reduction[J]. Acta Aerodynamica Sinica,2008, 26(1): 79-84.
[5]Viswanath P R. Aircraft viscous drag reduction using riblets[J].Progress in Aerospace Sciences, 2002, 38(6): 571-600.
[6]Han M, Lim H C, Jang Y G, et al. Fabrication of a micro riblet film and drag reduction effects on curved objects[C]//12th International Conference on Solid-State Sensors, Actuators and Microsystems. Boston: IEEE Electron Devices Society, 2003:396-399.
[7]Wang J J, Lan S L, Chen G. Experimental study on the turbulent boundary layer flow over riblets surface[J]. Fluid Dynamics Research, 2000, 27(4): 217-229.
[8]张成春, 任露泉, 王晶. 旋成体仿生凹环表面减阻试验分析及数值模拟[J]. 吉林大学学报: 工学版, 2007, 37(1): 100-105.ZHANG Cheng-chun, REN Lu-quan, WANG Jing. Experiment and numerical simulation on drag reduction for bodies of revolution using bionic scrobiculate ringed surface[J]. Journal of Jilin University: Engineering and Technology Edition, 2007,37(1): 100-105.
[9]刘志华, 董文才, 熊鹰. 雷诺数对沟槽减阻特性影响的数值分析[J]. 海军工程大学学报, 2007, 19(2): 6-11.LIU Zhi-hua, DONG Wen-cai, XIONG Ying. Numerical analysis of the effect of Reynolds number on drag reduction by grooved surface[J]. Journal of Naval University of Engineering, 2007,19(2): 6-11.
[10]Zheng Z C. Effects of flexible walls on radiated sound from a turbulent boundary layer[J]. Journal of Fluids and Structures,2003, 18(1): 93-101.
[11]Pavlov V V. Dolphin skin as a natural anisotropic compliant wall[J]. Bioinspiration and Biomimetics, 2006, 1(2): 31-40.
[12]Huang J C, Johnson M W. Boundary layer receptivity measurements on compliant surfaces[J]. International Journal of Heat and Fluid Flow, 2008, 29(2): 495-503.
[13]Fish F E. The myth and reality of Gray’s paradox: Implication of dolphin drag reduction for technology[J]. Bioinspiration and Biominetics, 2006, 1(2): 17-25.
[14]Li M T, Ren L Q, Lin Q P, et al. The mechanism of drag reduction around bodies of revolution using bionic non-smooth surfaces[J]. Journal of Bionic Engineering, 2007, 4(2): 109-116.
[15]ZHAO Gang, ZHAO Hua-lin, SHU Hai-sheng, et al. Simulation study of bionic jetting direction influence on drag reduction effect[J]. Advances in Nature Science, 2010, 3(2): 17-26.

