需求不确定条件下考虑通用航空的地面等待策略

朱士新

（中国民用航空局空中交通管理局，北京 100021）

通用航空和运输航空是民用航空的两翼。作为民航基础产业的重要组成部分，通用航空在社会发展、经济建设和公共服务等方面具有不可替代的作用。随着国家支持通用航空产业发展政策的陆续出台，中国通用航空将迎来快速发展的时期，日益增多的通用航空飞行会给原本拥挤的空中交通带来额外负担，造成更大延误。因此，从流量管理角度出发，考虑通用航空和公共运输航空的区别，有必要研究制定一套将通用航空纳入流量管理运行的方法。

地面等待策略是由空管部门制定实施的一种交通管理程序：航空器在起飞机场被分配延误并通过地面等待以平衡目的机场的容量和需求，其目的是减小空中等待和提高机场利用率。传统的地面等待策略未考虑通用航空带来的需求不确定影响，对所有航班采用延误统一均分的方法，当有通用航空器加入程序时容易造成空中盘旋等待，加大延误成本。

图1 通用航空机场程序示意图Fig.1 Schematic diagram of general aviation airport program

本文基于美国通用航空机场程序中的预留时隙思想（如图1所示）[1]，通过对通用航空飞行特点的研究和地面等待程序工作流程的调研，提出了考虑通用航空的改进型地面等待模型，可为管制员在实施地面等待时提供更加科学有效的延误及时隙分配决策支持，达到降低延误总成本，提高机场利用率的目的。

1 地面等待模型及其改进

1.1 问题描述

由于信息的不完整和复杂性，无法准确预测的因素和事件称为不确定性。在地面等待策略的制定和实施过程中会面临诸多不确定因素的影响，如天气的变化、航班的调整等。不确定性对机场容量和航班需求都会带来不可预测的扰动。现有对地面等待策略的研究大多把需求当作确定量，即程序中各个时间段内到达航班的数目确定且已知，而忽略了不确定航班对需求的影响。通常，需求不确定性的来源主要有航空器的突现、取消和漂移[2]三种，如图2所示。

图2 不确定航班的来源Fig.2 Sources of demand uncertainty

突现：在程序时间范围内到达但在程序制定时不存在的航空器，通常指通用航空飞行；

取消：航班取消造成到达序列出现程序预计之外的空时隙；

漂移：航空器漂移代表其偏离了指定的到达时间，主要原因是航路拥堵。

地面等待模型应充分考虑需求和容量的关联性：如果实际需求大于设置的到场容量，则于航班之前进行的地面延迟无法充分缩减空中等待。同理，如果实际需求小于设置的到场容量，则可能会使航班进行不必要的地面延迟从而降低机场的利用率[3]。所以，科学高效的地面延迟策略应该同需求的不确定性相互关联，只有当到场需求的设定值与实际的航班到场率比较接近时，才能在机场容量得到充分利用的同时又不会造成太多空中等待。

基于此，本文把单机场地面延迟策略问题看作是单服务台的排队问题，如图3所示，考虑需求随机容量确定的情形，引入通用航空飞行参量和机场空闲容量惩罚系数，借鉴传统容量确定型地面延迟模型建立改进型整数规划模型，旨在通过改进模型的构建和求解，生成一种优化的地面延迟策略，直接输出实现目标函数最小值时各个时段需要进行地面延迟的航班数量，从而使得在整个程序范围内的地面延迟费用和空中等待费用之和最少，同时时隙资源即机场容量能得到充分利用。

图3 到达航班的队列模型（单服务台排队系统）Fig.3 Queue model of arrival flights（single server queuing system）

1.2 模型假定

1）除起飞机场其他区域交通顺畅，航路上无阻塞情况，航班运行正常，无机械故障和人为操作失误；

2）为简化模型，假定目的地机场只有一条跑道，把机场当作单服务台排队系统；

3）本文考虑的是需求不确定下的单机场地面延迟模型，着陆机场的容量是整个空中交通网络的唯一受限元；

4）假定时间区间数T和程序开始时间均已知，且在每个时间段内机场的容许进场率是确定不变的；

5）为了确保应用地面延迟策略能得到最优解，假定计划在程序范围内到场的航班总数小于整个时间区间内目标机场的容量总和，但在某一时段内，降落在机场的航班数目大于该时刻的机场容量；

6）以先来先服务为原则，对航班组进行排序。按顺序确定序位的分配，如果有多个航班组竞争相同序位，该序位分配给优先级最高的航班组（见注）；

7）基于大量历史数据统计，假定突现航空器流服从泊松分布，即到达间隔时间按参数λ呈指数分布[4]。

注 航班优先级（从高到低）：豁免地面等待的航班；已经分配时隙的航班；等待分配时隙的航班。

1.3 模型建立

首先定义模型中的符号、参数变量如下：

T1，…，Ti，…，TN∈T 为 GDP 程序中具有同等期限的离散时间段；Ci为目标机场各时间段内的容量大小（airport acceptance rate，AAR），即可以容纳到达航班的数量；Si为计划在i时段内到场的航班总数；Q为机场到场需求的发生范围，即可选的到场需求样本的总数量；q∈Q为有通用航空加入的一个具体的到场需求样本；pq∈[0，1]为样本q发生的概率，服从泊松分布；Mg为单位时间内航班在起飞机场地面延迟成本大小；Ma为单位时间内航班在到达机场空中等待成本大小；Ms为单位时间内机场空闲容量造成的成本损失大小。

定义问题的决策变量：

Gi为i时段内进行地面延迟的航班数量。

辅助决策变量：

Fq，i为 i时段样本 q 中实际到场的航班总数；Aq，i为i时段样本q中发生空中延迟的航班数量；Xq，i为i时段样本q中通用航空器的到达量，即需求增量；φq，i为i时段样本q中到达机场的空闲容量。

目标函数

约束

其中：Gi、Aq，i、φq，i、Fq，i∈Z+。

目标函数分为3部分：第1部分是地面延迟成本，由决策引起，决策确定则该项费用确定；第2部分是空中等待成本，由通用航空器带来的需求不确定性引发；第3部分作为惩罚系数，是到达机场的空闲容量的损失成本[3]。

约束（1）表示，可能在i时段到达目的机场的航班，包括计划到场航班、通用航空器带来的需求增量和上一时段延后的航班，只有准时降落和进行地面延迟两种情况；约束（2）表示，i时段空中延迟的航班数目等于此时到场航班数目加上前一时段空中延迟的航班数目再减去此时所利用的机场到场容量。

当i=0时并不需要地面延迟和空中等待，所以初始条件G0=A0=0始终成立。求解该整数模型，即可得到实现目标函数最小值时各个时段需要进行地面延迟的航班数量。

2 模型求解及算例仿真

2.1 算法选择和流程

在地面延迟模型的求解中，如果模型中没有考虑需求不确定性的影响，传统的求解方法是启发式方法与专家系统相结合，虽然加快了模型求解速度，但是启发式算法是近似算法，往往无法得到最优解。在引入通用航空相关参量后，求解本文中建立的随机地面延迟整数规划模型，使用这种方法不能满足要求。因此，本文引入一种针对地面等待的随机动态算法，用以解决需求不确定性下地面等待模型的求解问题。

算法的计算步骤如下：

1）在某时刻，获取预计到达时间在此之后的T时间段内的航班列表，Q为在此时间段内可选的到场需求样本的总数量，q为有通用航空加入的一个具体的到场需求样本，pq为样本q发生的概率，服从泊松分布；

2）把程序规划总时间T划分为N个等同的时间区间 T1，…，Ti，…，TN；

3）根据Ti时段内进行地面延迟的航班数量和单位时间内航班在起飞机场地面延迟成本计算Ti时段内地面延误成本DGi；

4）根据Ti时段内样本q中发生空中延迟的航班数量和单位时间内航班在到达机场空中等待成本计算Ti时段内地面延误成本 DAq，i；

5）根据Ti时段内样本q中到达机场的空闲容量和单位时间内机场空闲容量造成的成本损失计算Ti时间段内由于空闲容量造成的惩罚损失ΔPq，i；

6）计算T时段内由于通用航空加入造成的所有损失，实现整个T时间段内的损失最小化；

7）根据 RBS（ration by schedule）优先级把时隙分配给航班，允许航空公司内部替换或取消；

8）更新容量通告，算法结束[5]。主要算法流程如图4所示。

2.2 求解过程

由于国内通用航空飞行有限，数据收集难度较大，本文的数据来源于Metron公司的机场需求清单（aggregated demand list，ADL）存档和数据库，实验选用旧金山机场实施地面等待策略某天8：00～12：00时间段内的数据。在GDP程序下旧金山机场的4条跑道中只有1条能够使用，故符合本文模型假定的单服务台排队系统情形。

具体实验过程如下：

1）根据程序内的航班时刻表和飞行情报，将选取的时间段10等分，分别为：

第一时段：08：00～ 08：24；第二时段：08：24～ 08:48；第三时段：08：48 ～ 09：12；第四时段：09：12 ～ 09：36；第五时段：09：36～10：00；第六时段：10：00～10：24；第七时段：10：24 ～10：48；第八时段：10：48 ～ 11：12；第九时段：11：12 ～ 11：36；第十时段：11：36 ～ 12：00。

2）依据所分时段，参照目标机场的实际情况设定初始状态数据，分别为：

图4 随机动态地面延迟算法流程Fig.4 Dynamic stochastic ground holding algorithm flow

C=[30 40 30 35 36 37 38 40 39 37]：目标机场各时段内的容量大小；

S=[24 33 23 31 30 34 29 33 32 25]：计划在各时段内达到的航班总数；

Q=[24 33 23 31 30 34 29 33 32 25]：机场到场需求的发生范围，即可选的到场需求样本的总数量。

3）描述样本q，画表，统计得出pq，输入数据。

对到场需求的随机性，本文采用样本描述的形式，将机场的突现航空器数量视为到场需求样本空间的离散型随机变量，并假定其分布率已知。具体描述如表1所示。

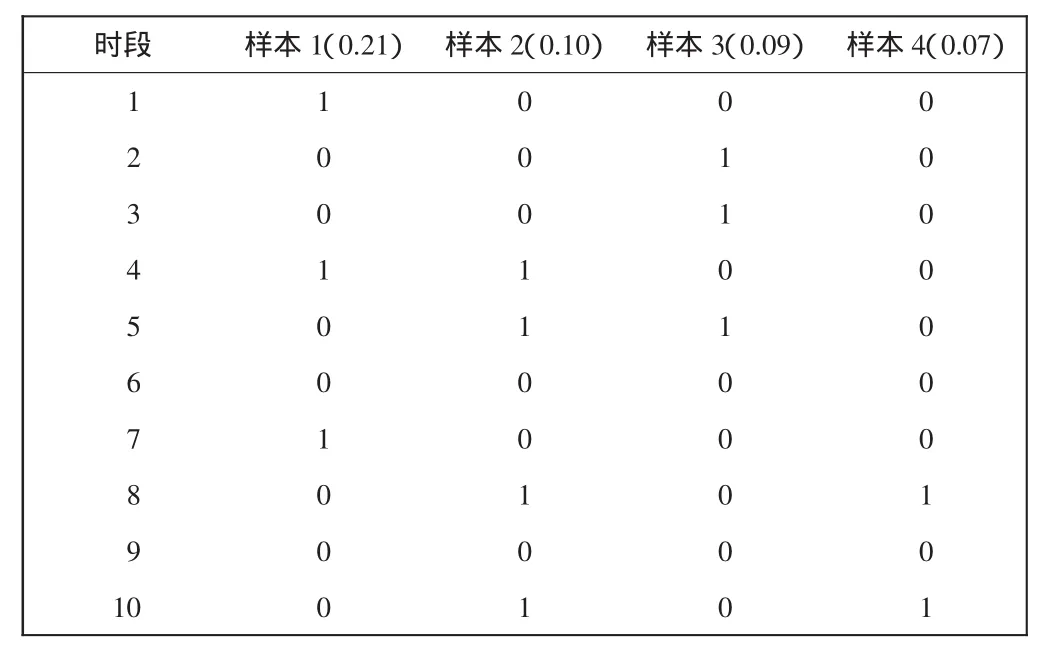
表1 有通用航空加入的到场需求样本描述Tab.1 Description of arrival demand samples considering general aviation

其中，样本q发生的概率服从泊松分布，分别为0.21、0.10、0.09、0.07。

4）定义：Mg=μ：单位时间内航班在地面延迟成本大小（元/h）；

Ma=3.5 μ：单位时间内航班在空中等待成本大小（元/h）；

Ms=0.6 μ：单位时间内机场空闲容量造成的损失大小（元/h）；

其中：Mg为标准参量；μ为有限大的任意实数。

5）在Matlab的新建M文件中构建线性规划模型并构造决策变量的价值向量和约束条件的4×10维系数矩阵和资源向量。

6）求解模型并输出决策变量X的值。

2.3 结果分析

输出的最优解是一个1×158的向量，其中：1～36行表示各时段实际到场的航班总数，37～76行表示各时段发生空中等待的航班数量，77～86行表示各时段进行地面等待的航班数量，87～112行表示各时段通用航空器带来的需求增量，113～158行表示到达机场的空闲容量。

根据矩阵中 Fq、Aq、G、Xq、Φq的排列顺序，选取决策变量G的值，如图5所示，并将决策变量的输出值代回模型进行分析，得到一组供参考的进场率设置值。

图5 优化前计划进场率的设置Fig.5 PAAR setting before optimizing

为表明优化效果，选取传统的单机场确定型地面等待策略，利用Matlab软件对模型进行仿真运算，输出结果如图6所示。优化前后的地面延迟架次、空中等待架次和机场空闲容量（向上取整），如表2所示。

计算结果表明：当有通用航空加入时，相比执行传统地面等待策略的情况，改进后的模型虽然增加了地面延误航班数，但都明显减少了空中等待航班数并提高了机场利用率。而经过模型的优化调整，更多的空中等待转化为地面延迟，进一步减小了延误成本。通过优化前后各项统计数据的比较分析，可以证明本文提出模型和算法的可行性和有效性。

图6 模型输出的优化计划进场率Fig.6 Optimal PAAR by model output

表2 优化前后各项数据统计结果Tab.2 Statistical results of optimization

3 结语

随着低空空域的逐步开放，通用航空将成为导致空中拥挤和航班延误的原因之一，本文针对有通用航空加入的地面等待问题，参考美国的流量管理程序并结合通用航空飞行特点，进行了考虑通用航空的地面等待策略研究。在模型构建中把航班到场需求当作随机量，同时引入对机场空闲容量的惩罚系数，选用随机动态算法进行求解，使输出结果更具公平性和有效性，最后结合算例比较优化前后效果，验证了本文研究成果的可行性。

如何利用本文模型进行深入研究，协调通用航空和运输航空的冲突，合理地配置时隙资源和间隔，力求将流量控制带来的不利影响逐步消除，将总体延误降至最低，这将是下一步研究的重点。

[1]METRON Aviation.General Aviation Airport Programs[EB/OL].[2011-12-20].http://www.metronaviation.com/solutions/traffic-flow-management/concepts/gaap.html

[2]BHOGADI N.Modeling Demand Uncertainties during Ground Delay programs[D].Mary Land：The National Center of Excellence in Aviation Operations Research（NEXTOR），2002.

[3]王来军，史忠科.需求随机型单机场地面等待问题的优化建模研究[J].计算机工程与应用，2004（34）:34-35.

[4] 关 钰.空中交通流量管理中地面等待策略问题的研究[D].成都：四川大学，2006.

[5]AVIJIT MUKHERJEE，MARK HANSEN，SHON GRABBE.Ground Delay Program Planning Under Uncertainty in Airport Capacity[C]//AIAA Guidance，Navigation，and Control Conference.Chicago，Illinois，August 10-13，2009.