混凝土单轴受压时的徐变损伤研究
刘国军,杨永清,郭 凡,李晓斌
(西南交通大学土木工程学院,四川成都 610031)
变形的时效性是混凝土的重要特性,时效性是指变形是时间的函数,变形随着时间的发展而逐渐变化的性质。这种时效性包括两个方面的变形特性[1]:一是硬化水泥浆体长期蠕变产生变形,这部分变形不对混凝土材料造成损伤;二是随着变形发展,材料内部的损伤不断地发展,混凝土内部裂纹不断扩展。混凝土的徐变在应力水平较低时,以水泥浆体的蠕变为主;而当应力较高时,以混凝土材料内部的损伤为主。
对混凝土徐变的研究[2]表明:混凝土持续应力较低时(小于0.4~0.5倍混凝土强度),徐变和应力呈线性关系;混凝土持续应力较大时(大于约0.5倍的混凝土强度),应力和应变之间将不再保持线性关系。
高虎等[3]开展了混凝土双轴压缩徐变试验,测定了多轴混凝土徐变试件的强度,比较了同龄期混凝土的受力强度,研究了混凝土在双轴压缩应力下微观切片的裂缝发展情况,认为低应力水平以下压缩徐变试件强度并不降低,其压缩徐变变形不以试件的损伤为代价。
当持续应力超过0.4~0.5倍的混凝土极限强度后,处于非线性徐变阶段。该阶段混凝土内部的初始微裂缝开始逐渐扩展,并将产生新的微裂缝,故非线性徐变特性和线性徐变有本质的区别,此时的徐变速率将变大。因此,单位应力作用下徐变度函数,与线性徐变明显不同[4]。
对混凝土持续高应力状态下的徐变研究[4-7]发现各种混凝土的长期强度约为瞬时强度的0.75~0.85倍,当长期持续的应力值高于长期强度时,混凝土产生徐变破坏。
1 非线性徐变的机理
在高应力作用下,混凝土非线性徐变的原因是混凝土材料内部裂纹不断扩展[2]。主要特征为:
1)非线性徐变阶段,混凝土既有微裂缝进一步扩展,因而徐变损伤相对于瞬时损伤有所增加,徐变损伤的演变又造成徐变值增加。当持荷应力超过混凝土的长期强度(约为0.8倍的混凝土强度)后,裂缝扩展迅速,徐变损伤的不稳定扩展将造成破坏。
2)徐变损伤分为界面裂缝的损伤和砂浆裂缝的损伤。当应力水平低于长期强度时,砂浆裂缝可忽略不计,此时徐变变形值是收敛的;当应力高于长期强度时,砂浆裂缝不断扩展,导致徐变损伤变形值发散,在短时间内将使材料破坏。
2 徐变损伤应变研究
林南熏等[7]建立了非线性徐变方程,混凝土的非线性徐变εbc采用总应力函数f(σ)计算,其表达式为

式中,R是混凝土的极限强度;φ(t,τ)是徐变度。当σ<R/2时,f(σ)=σ。
混凝土的徐变由可逆徐变b和不可逆徐变c组成,可表示为

林南熏进行了两组高应力下的徐变试验,得出可逆徐变函数fb(σ)和不可逆函数fc(σ)的计算式。测量出各级应力的弹性后效变形,作为可逆徐变变形εb(t,τ),并测量出各级应力的徐变变形 εbc(t,τ),则可得出不可逆徐变为

根据式(3),逐步分解出各级应力的不可逆徐变值。研究结果表明,当应力级不超过混凝土的长期强度时,应力与可逆徐变成线性关系,前苏联专家的研究中也得到了相似的结论[8],因而有

应力与不可逆徐变为非线性关系,采用式(5)逼近

非线性徐变的关系式式(2)可改写为
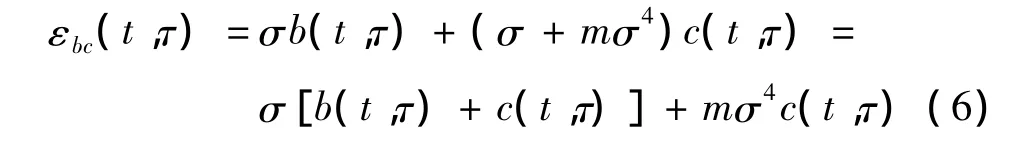
在式(6)中,等号右端第1项为线性徐变,是由于水泥胶凝体的蠕变产生,第2项为非线性徐变,主要是由于混凝土微裂缝的扩展导致。同时可以看出,混凝土在低应力作用时,也存在少量非线性变形[2,7]。
本文将非线性徐变按持续荷载值σ(t0)与混凝土强度fc(t0)的比值分为两种情况,分别对徐变的损伤应变进行计算,t0表示加载龄期。
1)σ(t0)/fc(t0)<0.8,且 σ(t0)/fc(t0)的最小值在0.4~0.6之间时,在荷载的持续作用下徐变值会趋于收敛,最终稳定于极限值。
林南熏将混凝土的不可逆徐变分为线性徐变和非线性徐变两部分。非线性徐变是混凝土内部裂缝开展导致的结果,本文将不可逆变形中的非线性徐变定义为徐变损伤 εcd(t,τ),表示为

2)当σ(t0)/fc(t0)≥0.8时,混凝土高应力荷载作用下,混凝土试件持续一段时间后将因徐变的发散而破坏。一般来说,混凝土试件的长期抗压强度约为0.8fc(t0)。李兆霞[8]通过在持续高压应力下的混凝土徐变破坏试验,研究了混凝土徐变破坏的规律,研究时使用了4组试件,每组2个试件,4组试件分别加载的应力水平为83%,85%,90%和95%。4组试件徐变破坏区域均发生在试件中间部位20 cm的均匀应力区范围内,试验结果见表1。
Bazant等[9]试验研究了在持续高应力状态下的徐变破坏,给出了在徐变状态下的混凝土试件的持续寿命,见表2。
可见,当σ(t0)/fc(t0)≥0.8,混凝土将在荷载作用下发生徐变破坏。此时徐变破坏是因混凝土内部裂纹扩展导致的。

表1 4组试件徐变破坏测试结果[8]
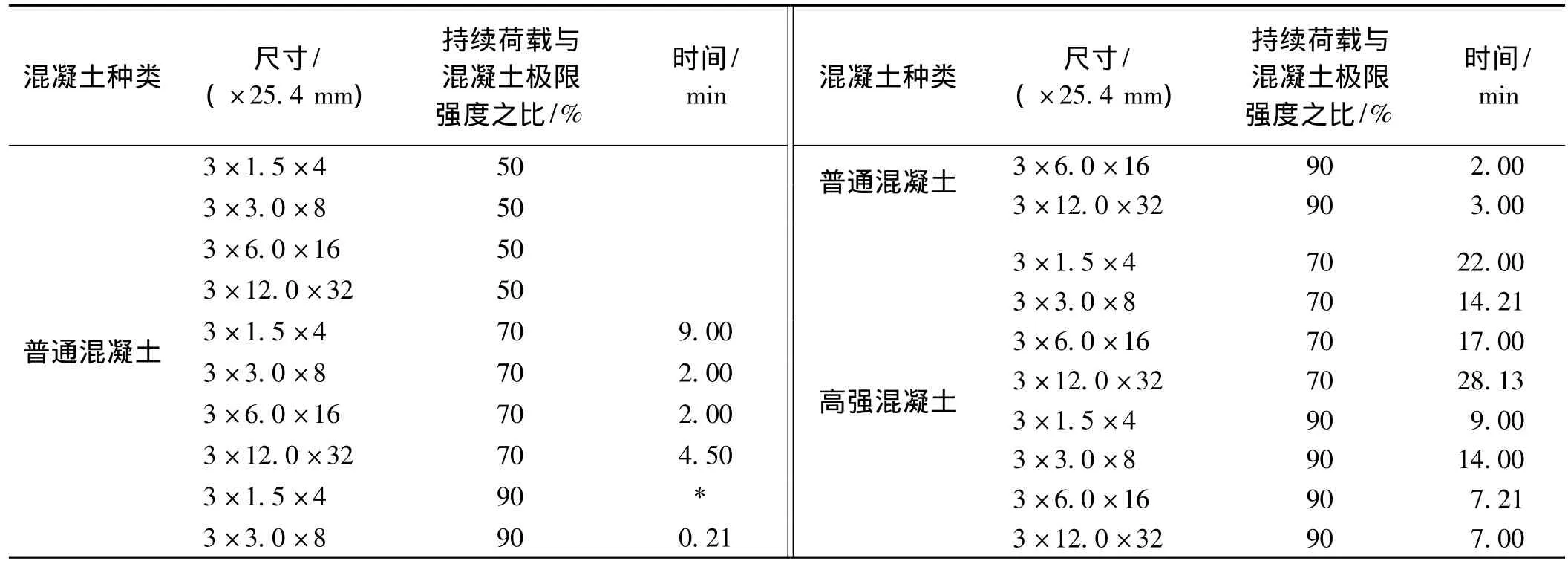
表2 混凝土在高应力持续荷载作用时的寿命[9]
3 徐变损伤的计算和存在的问题
由以上分析得混凝土徐变损伤应变的计算公式为
当σ(t0)/fc(t0)的最大值在0.4~0.6之间时

当σ(t0)/fc(t0)<0.8,且σ(t0)/fc(t0)的最小值在0.4~0.6之间(包括等于)时
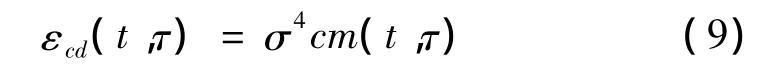
当σ(t0)/fc(t0)≥0.8时

式中,εmax为混凝土在一次加载破坏时的极限应变值。
假设非线性徐变公式中系数mc(t,τ)=1,拟合曲线见图1,横坐标表示持续荷载作用下的应力与混凝土极限强度的比值,即σ(t0)/fc(t0);纵坐标表示混凝土的徐变损伤度,徐变损伤度表示混凝土损伤徐变的应变值εcd(t,τ)与混凝土在一次加载破坏时的极限应变值εmax的比值。
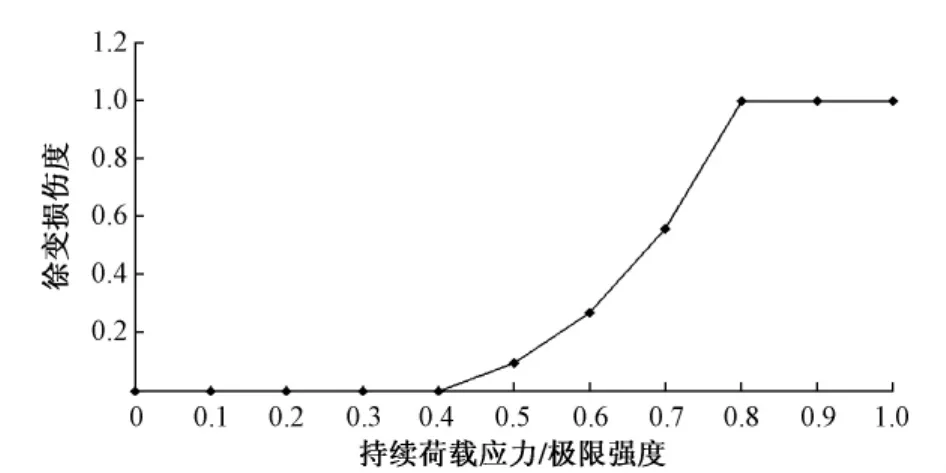
图1 徐变损伤度曲线
徐变损伤度反应了混凝土在非线性徐变时,混凝土内部损伤的发展情况,非线性徐变主因是混凝土内部微裂纹的产生和扩展。
4 结论与建议
1)在应力较低时,混凝土的徐变变形属于线性徐变阶段,以水泥胶凝体的流变为主,不以损伤为代价。该阶段,混凝土内部微裂缝的发展可忽略不计。因此在线性应变阶段,可近似认为混凝土的徐变损伤度为0。
2)在应力较高,处于非线性徐变阶段且应力低于混凝土的长期强度时,混凝土徐变可分为线性徐变和非线性徐变两部分。非线性徐变主要是由于混凝土内部裂纹的扩展导致。此阶段,混凝土的裂缝虽然扩展,但将达到稳定的平衡状态,故该阶段的徐变变形值将最终收敛。
3)在应力大于混凝土的长期强度时,最终混凝土将徐变破坏。该阶段,混凝土的徐变主要是由裂缝的产生和扩展导致的,且裂缝无法达到稳定状态,故此阶段混凝土的变形是发散的,最终导致混凝土破坏。因此在应力大于混凝土的长期强度时,认为混凝土的徐变损伤度为1。
在应力较高,处于非线性徐变且应力低于混凝土长期强度时,损伤徐变量的计算方法仍需要大量的试验研究,本文依据文献[8],并假设非线性徐变系数为1时,给出了简化的徐变损伤度曲线,需要对该曲线进行更深入的研究,例如要研究不同持续应力、不同加载龄期、持续不同时间的混凝土试件的损伤应变规律。
[1]郭少华.混凝土蠕变损伤分析模型[J].西安建筑科技大学学报:自然科学版,1995,27(3):299-303.
[2]李兆霞.混凝土非线性徐变理论的研究[J].河海科技进展,1991,11(2):26-33.
[3]高虎,刘光廷,陆风崎.混凝土双轴压缩徐变试验初步研究[J].清华大学学报:自然科学版,2001,41(11):110-113.
[4]NEVILLE A M,DILGER W H,BROOKS J J.Creep of plain and structural concrete[M].London:Construction Press,1983.
[5]SMADI M M,SLATE F O,NILSON A H.High-medium and low-strength concrete subject to sustained overloads-strains[J].Strengths and Failure Mechanisms,1985(9):657-664.
[6]童智洋.混凝土收缩徐变对连续曲线箱梁桥的受力影响[J].铁道建筑,2010(6):14-15.
[7]林南薰.混凝土非线性徐变理论问题[J].土木工程学报,1983(1):16-23.
[8]李兆霞.高压应力作用下混凝土的徐变和徐变破坏[J].河海大学学报,1988(1):109-112,129.
[9]BAZANT Z P,XIANG Yuying.Crack Growth and Lifetime of Concrete under Long Time Loading[J].Journal of Engineering Mechanics,1997,123(4):350-358.

