S注入法选线局限性研究
李俊,丁凡,王科,王纪斌,徐云龙
(许继电气股份有限公司,河南 许昌 461000)
1 问题的提出
在我国6~35 kV配电网中,大多数电网采用小电流接地方式。电网中若发生单相接地故障,可允许电网继续运行1~2 h,随着电网容量的增大,电容电流也随之增大,电流经过消弧线圈接地方式被广泛使用,但其削弱故障特征却对接地保护装置构成了挑战。
1998年,山东工业大学桑在中等人提出了向电网中注入信号的方法,通过对注入信号进行循迹。此后,许多人都在此基础上进行了深入研究,针对注入信号的形式、频率及信号的接收等问题也提出了一些改进优化的方法(如注入信号编码、降低S注入信号频率、双频率注入法、带有小波滤波算法的窄带通滤波器等)。另外,对于注入信号的监测,一般需要工作人员手持信号接收器沿故障线路探测,这样会拖延时间,可能会导致故障进一步扩大。所以,一些学者提出在架空线路沿线隔一定距离装设信号探测器,基于电网的模型确定故障的区段。
这种主动式信号注入法定位虽然克服了以往多数故障装置利用故障发生后监测特征信号的被动局面,但它的应用也有一定的局限性,严重影响了选线与定位的实现。本文试图用仿真的方法分别讨论过渡电阻、线路长度对选线、定位的影响。给出了具体的仿真曲线,分析了仿真结果后,总结出基于S注入法选线与定位的应用局限。
2 S注入法基本原理
S注入法的基本原理如图1所示。在图1中,信号源接在变电所母线的PT二次侧,通过检测PT开口三角的电压判断是否发生单相接地故障并进行鉴相。在发生故障时,由于PT的某相相当于被闲置,所以,无需添加任何系统设备,电源与系统仅靠电磁联系,没有绝缘的问题。将一定频率的信号注入该相的母线,通过各个分支处及线路中的探测器反馈的接收信号的情况来进行接地故障的选线与定区段。
当发生金属性接地故障时,对地的分布电容对注入信号的分流作用可忽略不计,注入信号的流通路径如图1中单线箭头、虚线所示。
然而实际情况并非这么简单,在发生故障前、后,均可以看出有分布电容的存在,如图1中的C3-1、C3-2,它的大小与线路长度成正比,当线路较长、过渡电阻并没有那么理想时,无论是非故障线路还是故障后线路,它们的分布电容都会对注入的电流信号起分流作用,削弱选线和定位的效果,如图1中的双线箭头、虚线所示。下面的仿真中将会对其情况进行分开讨论。
注入信号选取有一定的原则,首先不能与基本频率及其频率的倍数相同,否则,注入信号将会淹没在基波及其谐波中;其次,不能影响通信及其他信号的正常工作。所以,对注入信号的基本要求可总结为:躲过基波及各次谐波,

式中:fn为某次谐波;fzr为注入信号频率。
3 过渡电阻与线路长度对选线影响的仿真
3.1 过渡电阻对选线影响
用PSCAD搭建的仿真模型如图2所示。其中,传输线选为Bergeron模型,它是基于行波原理的常频率模型,它能准确模拟线路稳态的阻抗或导纳。在图2中,I1~I4分别代表4条出线线路上的电流,4条出线长度设为13,18,21及11 km,分别带不同大小的纯阻性负载。注入电流源电流10 A,初相角为0,频率为220Hz。线路t=0.1 s发生故障,并持续至仿真结束,在t=0.2 s时开始注入信号电流,以便故障干扰减弱后利于观测。
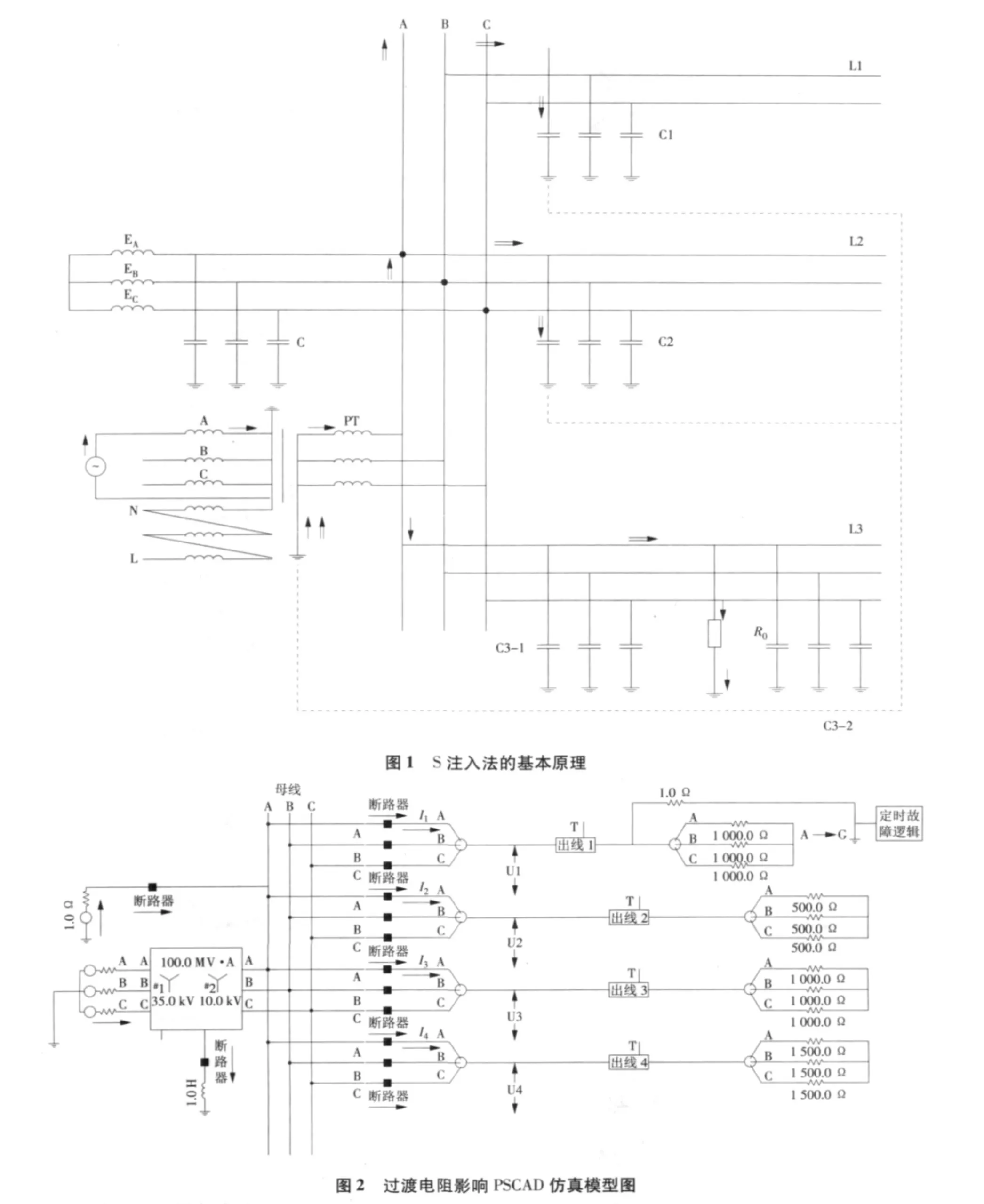
当过渡电阻R0=50Ω时,仿真结果如图3所示。
需要说明的是,图中稳定波形的幅值不能代表实际中的电流大小,这是因为在滤波器的作用下幅值会有畸变,所以,该仿真中注入信号的功率也没有实际中的那么大,但其波形不变,且每个电流所经过的带通滤波器参数相同,即能准确反映出其比例。其中,t=0~0.1 s的振荡是由于电源上升至稳定值造成的,线路在t=0.1 s发生单相接地故障有较大幅值的高频电流存在,至t=0.2 s时,待干扰逐渐变小后,注入频率为220Hz的电流,t=0.2 s后是观察重点。从仿真结果可以看出:故障线路故障相电流明显大于非故障线路电流(约为40倍),选线准确率高。
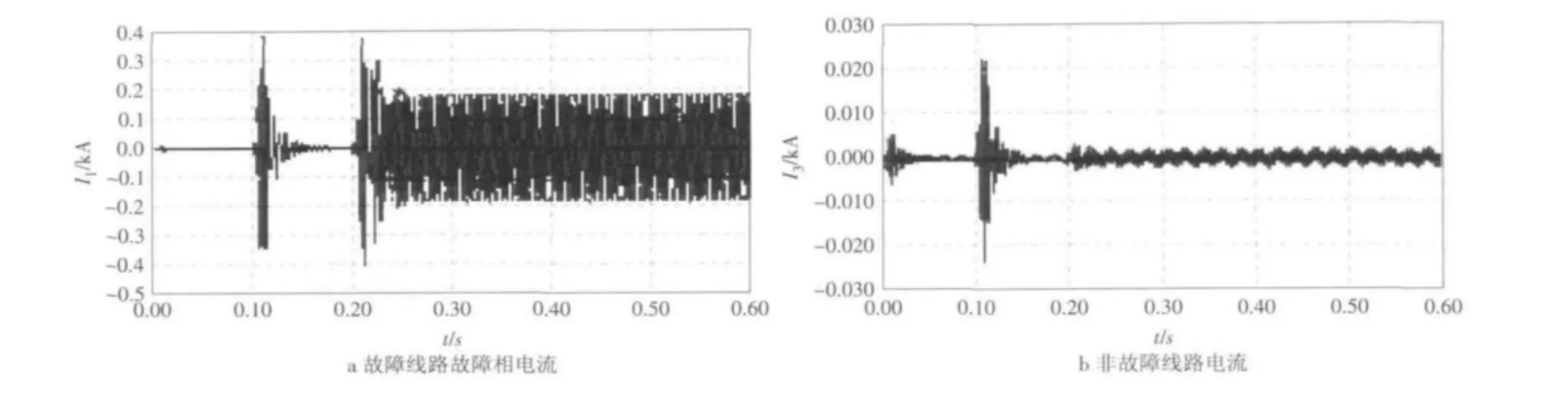
图3 过渡电阻为故障相电流与非故障线路电流对比
当R0=200Ω时,过渡电阻为200Ω故障相电流与非故障线路电流对比如图4所示。
上述仿真结果表明:故障相故障电流急剧减小,但仍是非故障线路电流的20倍左右,也能准确寻出故障线路。
当R0=1 000Ω时,过渡电阻为1 000Ω故障相电流与非故障线路电流对比如图5所示。
故障线路故障相电流为非故障线路的5倍,为同一个数量级,区分的不明显,不易选线。上述问题也说明了在频率为220Hz的注入信号下,当过渡电阻大于1000Ω时,区分度不明显,选线困难,容易造成错判。
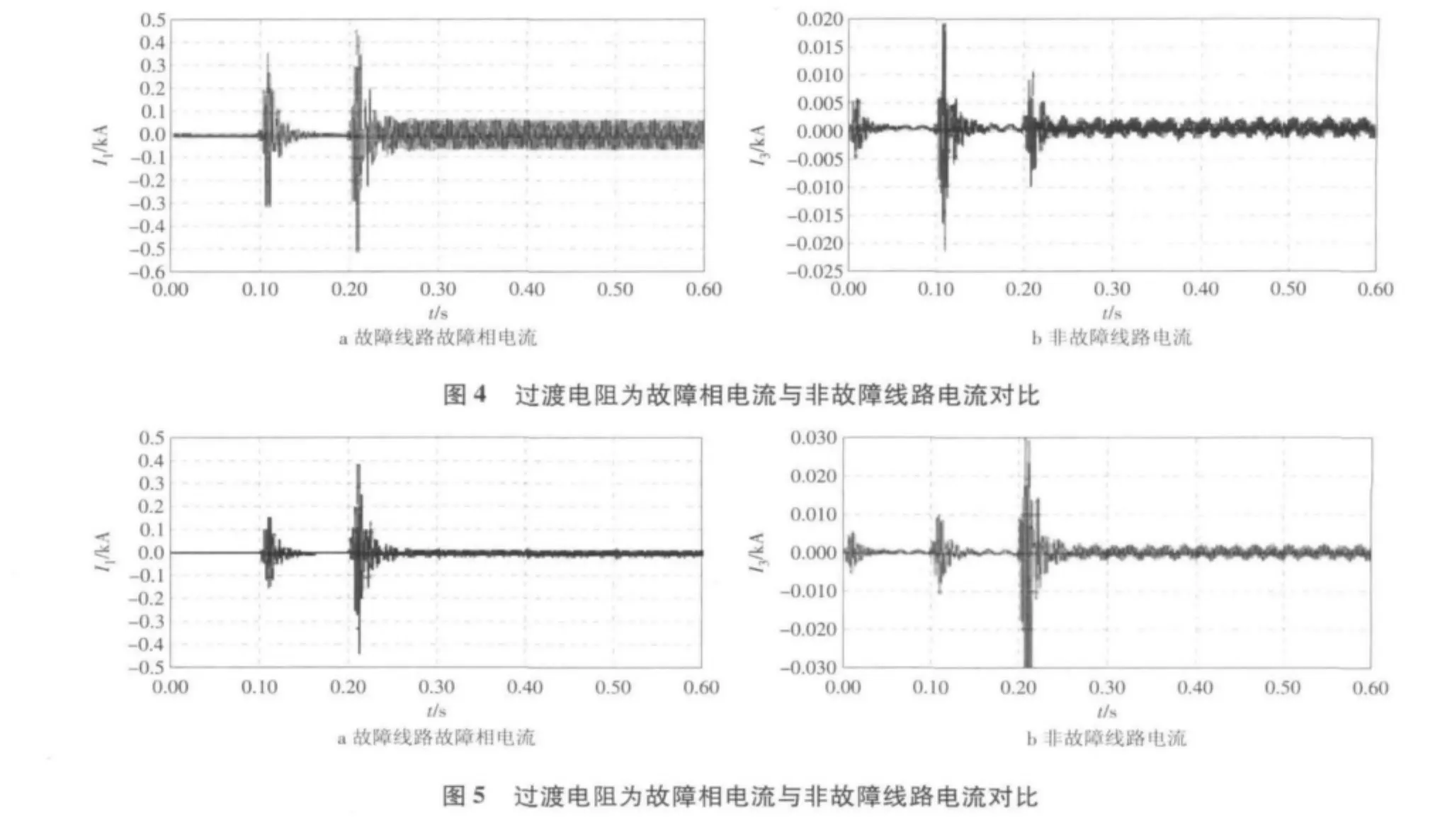
通过修改注入信号的频率,可以得到在不同过渡电阻下故障线路故障相电流与非故障线路电流的比值,将结果记录并拟合出其关系曲线如图6所示。
其中:横坐标代表电阻值;纵坐标代表电流比值;y1,y2,y3,y4,y5,y6,y7,y8和y9分别代表 20,40,60,80,120,180,220,280 和 320Hz。
3.2 线路长度对选线的影响
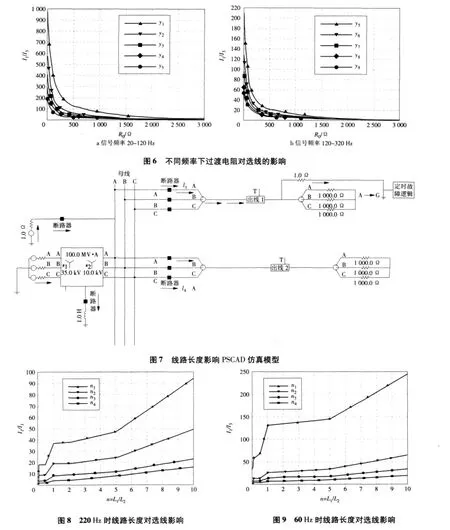
对仿真模型稍作修改,是为了更容易理解,这里只仿真了2条出线的情况,线路长度影响PSCAD仿真模型如图7所示。
上面的模型参数不变,在过渡电阻不变、2条出线长度相对变化的情况下做出仿真,下面仅分别以典型的频率为60Hz和频率为220Hz为注入信号来考虑:设L1为故障线路,L2为非故障线路,用n=L1/L2来定义2条出线长度的比例,通过改变n进行仿真,结果显示如图8所示。60Hz时线路长度对选线影响如图9所示。
其中:横坐标代表n,代表2条线路的相对长度比例;纵坐标代表故障线路故障相与非故障线路的电流比值。图8中的n1,n2,n3,n4分别对应的过渡电阻是100,200,500,1000Ω,图9 中的 n1,n2,n3,n4分别对应的过渡电阻是 100,500,1000,2000 Ω。
仿真结果分析:
(1)对于图6中的低频率部分(20~120Hz),当过渡电阻较小时,故障电流明显大于非故障电流。随着过渡电阻增大急剧减小,当频率较低时,线路容抗XC=1/jωC(式中:XC为线路容抗;ωC为角频)较大,非故障线路对注入信号的分流作用较小,随着过渡电阻的增大,分流作用越加明显,直至无法区分。值得指出的是,线路对地的容抗数量级较大。相关文献指出,频率在60Hz,220Hz,线路长度为20 km的情况下,线路的容抗试验值为3.38kΩ,分流电路支路电流为曲线,式中:I为分流电
R路支路电流;R为分流电路支路电阻。在仿真的过渡电阻范围内,比值恒大于1。
(2)对于图6中高频部分,随着频率的升高,分流作用凸显,表现为曲线随着频率的升高逐渐降低,同时也可以看到,在过渡电阻在500Ω时,60 Hz的电流比为50,而120Hz的电流比仅为10~20,所以,降低频率的方法可有效增大注入法的适用范围。
(3)从图8、图9可以看出,在出线长度比n=0.5~5.0时,仿真结果与前面的结果类似,即2段线路在长度差别的不大且在过渡电阻不大的情况下,各个频率的信号选线结果比较理想;当n<0.5时,即故障发生在较短线路上时,故障线路不易区分,而当n>5时,即故障发生在较长线路上时,故障却容易区分;原因是n较小时非故障线路长,导致总的对地电容的较小,容抗小,特别是经一定过渡电阻接地时,分流的作用很明显,区分度不大,反之,分流作用减弱,区分度增强。仿真结果说明,选线准确性与出线的相对长度有关,其中,若线路差距较大,发生在较长线路上的故障最易选出。
4 线路长度对定位的影响仿真
有关学者对水泥杆塔过渡电阻的试验研究表明,在干燥的冬天,其电阻多为10~20 kΩ,而在潮湿多雨的夏季,其电阻多为3 kΩ;在故障进行定位时,有必要考虑经水泥杆塔接地的定位有效距离问题。
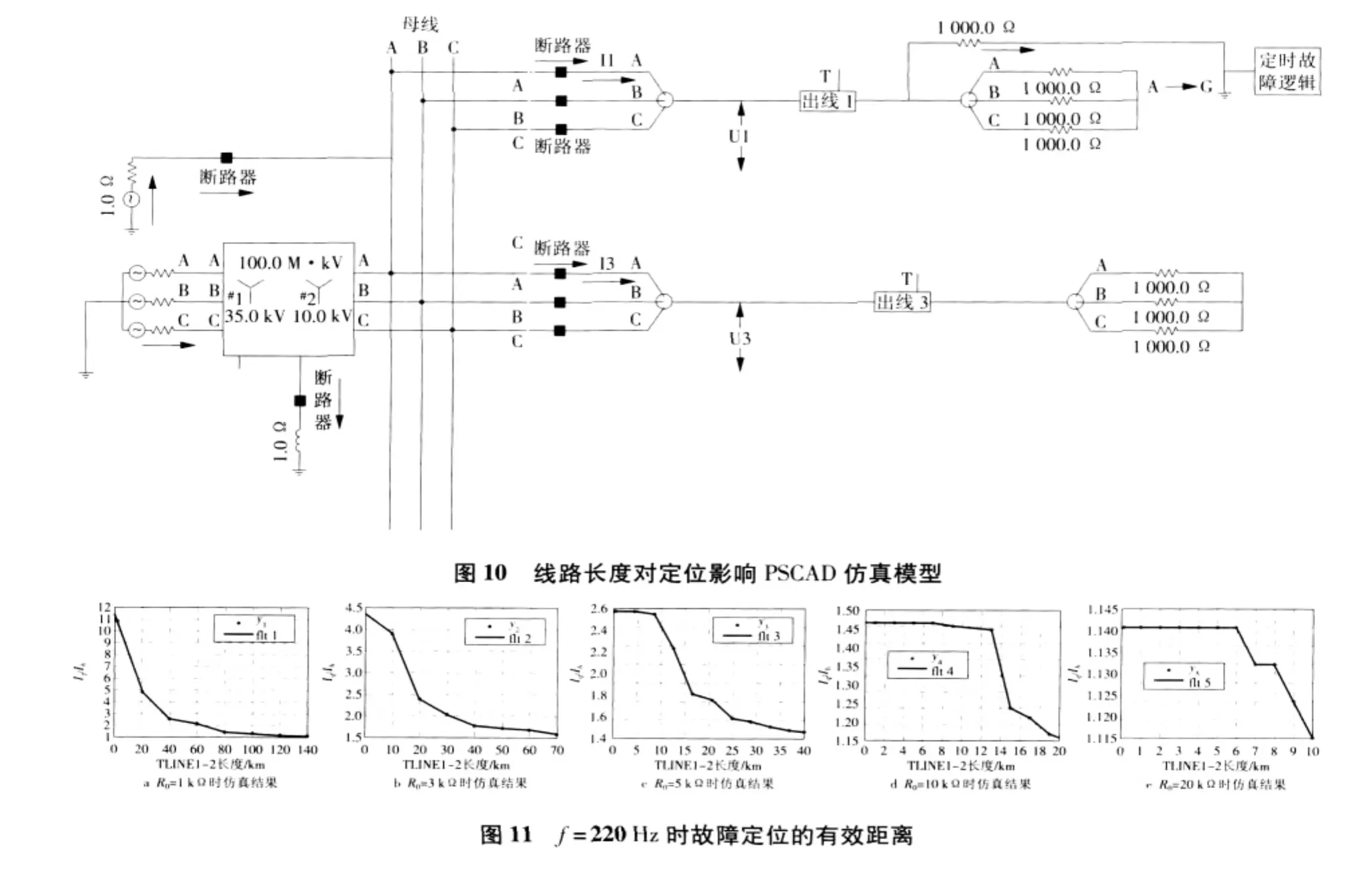
与上述模型均相似,唯一不同的是线路L1被分为2段:TLINE1-1和 TLINE1-2,通过改变TLINE1-2段线路的长度来研究线路长度对故障定位的影响。值得注意的是,作者考虑的是故障点前、后电流的变化,为了方便分析,可设定故障点前线路的长度不变,令TLINE1-1长度保持不变,甚至可将TLINE1-1去掉,即忽略故障前分布电容的影响,使仿真结果更为明确,如图10所示。
下面以典型的220 Hz为例进行仿真,如图11所示。
其中:y1,y2,y3,y4,y5对应的过渡电阻分别为1,3,5,10,20 kΩ。横轴为 TLINE1 -2 的长度,纵轴为故障点前、后电流值之比Iq/Ih(其中:Iq代表故障点前电流;Ih代表故障点后电流)。
仿真分析:
(1)随着线路的增长,容抗减小,逐渐接近过渡电阻,甚至小于过渡电阻,区分效果变差,定位的效果不明显,当故障点前、后电流比值小于2时,可认为电流没有发生突变,定位失效。
(2)故障定位的有效距离随过渡电阻增大而减小。对于20 kΩ的过渡电阻,频率为220Hz信号几乎没有定位能力;对于1 kΩ与3 kΩ的过渡电阻来说,注入信号频率为220Hz,定位的有效长度也都在60 km和30 km以上,这对于10 kV电网来说已经足够了。
5 总结与展望
(1)注入信号循迹法思路新颖,不依靠故障信号的特征,但在实际应用中有其局限性。从上述仿真结果来看,选线的条件要比定位的条件苛刻,对于1 kΩ以上的过渡电阻,采用信号注入选线方法无能为力。而用于定位时,在过渡电阻10 kΩ及以上经水泥杆塔接地的情况,其有效距离十分有限。
(2)在注入不同频率的信号时,不可避免地引入了一些谐波,即使其在电能质量要求范围之内,也会影响到对注入信号的提取,特别是在故障电流信号区分不明显的时候。同时,降低频率的方法虽有效地增加了选线及定位的效果,但其相比于注入频率为220Hz的信号引入的谐波更多,低频率信号注入法也增大了电源制造的难度,增加了成本。本文没有考虑具体电流的大小及谐波对选线和定位的影响,上述仿真条件较实际要理想得多。
(3)针对上面的选线瓶颈,许多学者进行了研究,值得一提的是,利用行波法进行选线是个比较新的研究方向。同时,针对水泥杆塔对故障定位影响,已有学者提出采用注入直流信号的方法来消除分布电容的分流作用,不过其对信号的检测是个难点,还未能应用于实际,但却是个大胆的尝试。
[1]王新超,苏秀苹,张丽丽,等.短暂扰动注入法对于小电
流接地系统线路状态在线监测的探讨[J].电力系统保护与控制,2010(6):141-145.
[2]张慧芬,张帆,潘贞存.基于注入信号法的配电网单相接地故障自动定位算法[J].电力自动化设备,2008(6):39-43.
[3]王慧,胡珂,桑在中.“S注入法”与电压互感器的特殊接线方式[J].继电器,2004(3):26-28.
[4]张慧芬,潘贞存,桑在中.基于注入法的小电流接地系统故障定位新方法[J].电力系统自动化,2004(3):64-66.
[5]马佳,余文辉,车伟扬,等.基于改进的S注入法的新型树状配电网故障检测装置[J].继电器,2002(10):51-54.

