不同拉压模量土工格室有限元模拟

屈成忠 蔺慧南

(东北电力大学建筑工程学院，吉林吉林 132012)

0 引言

土体是一种非常特殊的材料，其受拉和受压后所表现出的力学性能是非常不同的，这就表明它的抗拉和抗压强度相差就会很大，试验证明土体的抗拉强度为其无侧限抗压强度的12%～25%。土工格室正是弥补了土体抗压但是却不抗拉这一缺陷，目前的研究多是将土工格室假设为材料在拉伸、压缩时其弹性模量相等。实际上，土工格室在拉伸、压缩时其弹性模量存在较大差异。因此，采用经典力学对其进行求解，存在一定的误差。所以此次将不同拉压模量理论应用于土工格室的模拟，使结果更吻合材料特性。

1 理论基础

1.1 不同拉压模量理论基本概念和基本假设

国内外的许多学者在对基本概念和假设进行了充分研究的基础上，提出了不同拉压模量这一理论，对于解决单向应力和有限元分析给出了新的研究方向。各种物质都有不同的属性，在荷载的作用下会发生不同的应力和应变曲线，所以讨论拉压模量的不同变化能更准确的对不同材料和属性进行模拟[1]。

1)在实际的模拟中对于具有不同的拉压模量属性的材料其数学模型是很难建立的，为了更好的解决这一问题，受拉和受压的关系用双线性模型来表示，如图1所示。在σ＞0和σ＜0区域中材料的应力和应变关系呈现的是非线性的关系，为了方便程序中的计算故简化为线性关系。

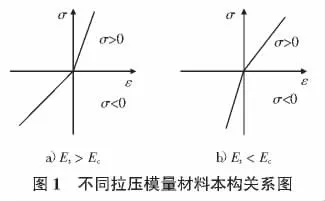
2)模拟的前提是假设物体内部属性连续、材质均匀并且是各向同性的弹性体。要符合介质的内在相关联性并在弹性范围内形变小的规律，定点上的主应力符号不同那么在与之相对的方向上弹性性质也不同。所以根据以上的方面不同拉压模量理论的应力和应变方程也与经典弹性理论是不同的。

3)假设沿各个方向的弹性性质材料的弹性模量和泊松比在σ＞0时，均为Et(材料拉伸时的弹性模量)和γt(材料拉伸时的泊松比);在σ＜0时，各方向均为Ec(材料压缩时的弹性模量)和γc(材料压缩时的泊松比)。

4)考虑经典弹性理论和材料的不同拉压模量，普遍情况要根据主应力符号是否相同来划分点(或区域)，通常情况下符号相同划分为第一类点(或区域);符号不同称为第二类点(或区域)。在第一类点中，不同拉压模量理论和经典弹性理论在公式表达的方面是完全相同的;相对于第二类点来讲，则要将Et，γt和Ec，γc应用于物理方程中。

1.2 土工格室的力学性能

1)土工格室抗剪强度的计算。

传统的模拟中会将土体和土工格室看作是完整的结构体，虽然其完整的强度会远远大于内部填土和外部土体，但是摩擦力是不变的。粘聚力cr在变化的过程中会有所改变，这一过程是随着土工格室对路堤加固作用而不断增加的，由以下公式表达:

其中，Kp为填土所受的压力;Δσ3为土工格室的内壁对填土产生的压力。

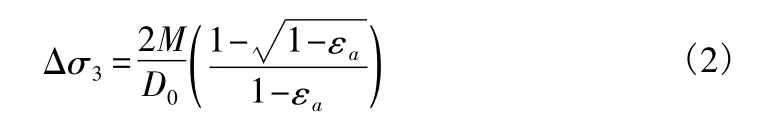
其中，εa为竖向荷载;D0为土工格室的原始格距;M为土工格室在竖向荷载εa下产生的压力，粘聚力cr从式(1)中可得出，设定内摩擦角不变。

2)土工格室弹性模量的计算。

通过三轴压力测试可知土工格室对土体有很强的加筋作用，采用杨氏模型来模拟路堤中土工格室的加筋作用，Madhavi Latha通过下列的方程对模拟系数进行规范。

其中土工格室本身所具有的抗剪性是影响加筋效果的重要参数:

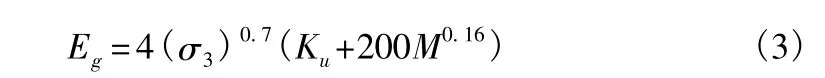
其中，Ku为加筋土体模型的刚度系数;M为土工格室生产过程中的切割系数，kN/m;σ3为土工格室内部填土产生的压力，kPa。

以上式(3)当中的各项参数参照邓肯—张准双曲线模型的各项参数，并且M的值要与土工格室在压力±2.5%的变化下所得结果相同[2]。

2 本构关系与有限元模型的建立

2.1 土体和土工格室的本构关系

土体是一种特殊的材质，内部颗粒是非均质和各相异的一种混合体，性质复杂且无具体的规律性可言，最重要的是应力和应变关系呈现非线性的特征。经常被使用的模型有:线性弹性模型、弹性非线性模型和弹塑性模型等等。土体的材料本身的受拉屈服强度很小，受压屈服强度很大，试验数据表明静水压力和偏应力可以导致土体的塑性体积变化(剪胀)，所以选取ANSYS中广泛应用于岩土模拟并能准确描述材料属性的D-P模型。粘结力、摩擦角和膨胀角(本文膨胀角为0)为D-P模型中主要的参数[3]。

土工格室的受力特点是既能受拉，又能受压，并且土工格室的抗拉强度和弹性模量相对于土体来说是比较大的，在应变较小的情况下拉伸曲线是呈直线状态的，考虑到土工格室与其他土工织物不同的三维立体网状结构，所以其本构关系不是完全弹性而是近似地看作线弹性。压缩模量是通过现场取原状土进行实验室有侧限压缩实验得出的，弹性模量要远大于压缩模量。地勘报告中，一般给出的是土的压缩模量Es，而一般不会给出弹性模量E。通过实验土工格室与内部填土的压缩模量也可求。数值计算中，有两种取法:

1)按弹性理论推出的弹性模量与压缩模量的关系E=Es[1－2v2/(1－v)]，可以计算出所需要的弹性模量;

2)根据经验取E=2.0Es～5.0Es，反复试算确定弹性模量;两种方法各有优点，第一种可以很方便的算出弹性模量，但与实际情况的弹性模量有一定的差别;第二种需要试算多次才能找到所需要的弹性模量，但比较符合实际情况。

2.2 有限元模型的建立

以往的研究将土工织物模拟成抗拉强度高，但是抗压强度却很小的单元，所以通常会选用刚度很小的薄膜单元进行模拟，最普遍的就是采用受拉的Shell63薄膜单元，但是土工格室除了本身的力学性能外还要考虑内部填土的受拉和受压作用，不能简单的模拟，其本身的高度也起到了一定的抗压作用。土体的材料选取拥有8节点的三维实体单元Solid45，路堤和地基的土体用Drucker-Prager准则进行约束。由于格室内填料设为经过充分的压实所以接触是充分的，可不考虑土工格室与土体产生相对滑移。但这并不能完全的模拟土工格室与土体的形变，因为土工格室自身所具有的高度，加上内部填土的作用，所以应将土工格室看作有高度的实体，利用接触单元将这部分相连接。研究对象为一个铺设土工格室的路基断面。取1/2模型。路堤尺寸为顶面长和宽为6 m，路堤高度4 m，下部长和宽分别为10 m，6 m;路堤基底长、宽和高分别为30 m，6 m和12 m;路堤的剖面图和有限元模型见图2和图3，土工格室与土体的各项材料属性和参数如表1所示[4]。

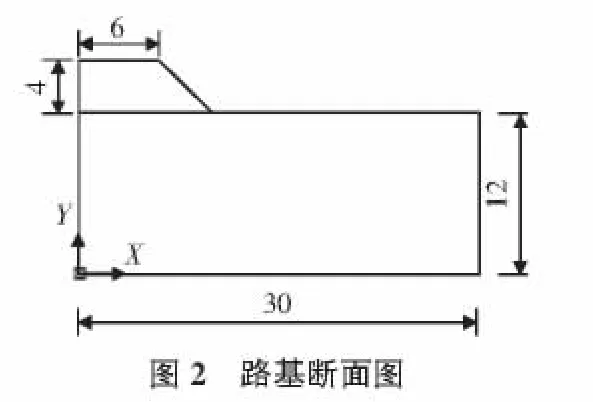
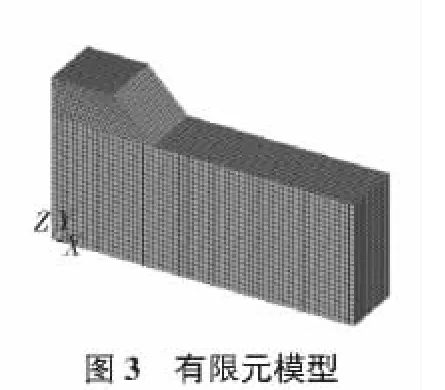
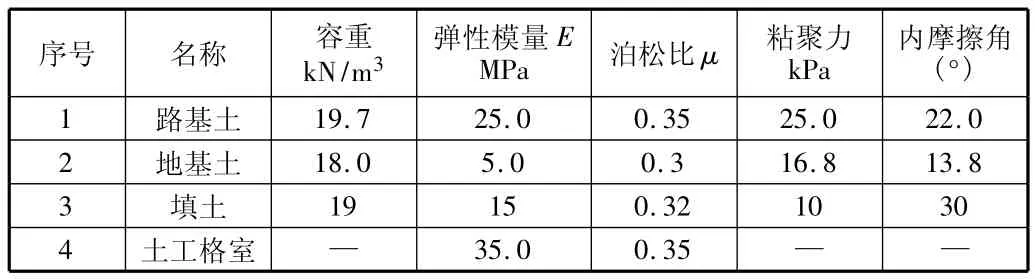
表1 土体及土工格室主要材料参数

3 计算结果分析

在选取的路堤中铺设一层土工格室，并且采用不同的方法模拟沉降、侧向位移和应力变化，具体结果见表2。

表2 铺设一层土工格室后的路堤各项参数变化

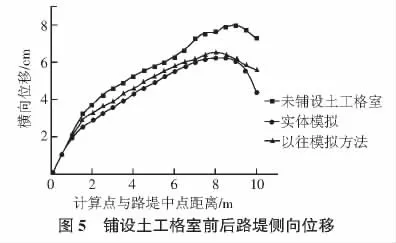
通过图4可知在路堤中铺设一层土工格室后其中点的沉降量与用以往的模拟方法相比减少了2.65%;采用实体模拟沉降量减少了38.27%。从图5可知路堤最大侧向位移发生在距离路堤中点9 m处，两种方法分别减少了22.81%和22.55%，差别并不显著。

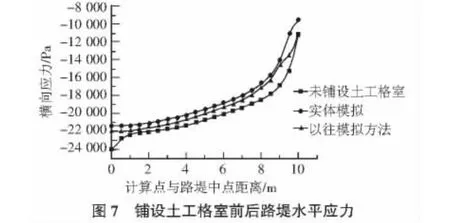
路堤的竖向应力和横向应力最大变化在路堤的中点，由图6可知以往的模拟方法和实体模拟竖向应力分别减少为25.21%和33.88%，如图7所示横向应力分别减少8.58%和10.78%。

4 结语

1)根据经典弹性理论，当假设某一物体的属性是连续并且均匀的、各向同性的、完全弹性的，位移和形变是微小的，无初始应力。所以在模拟土工格室与土体的变化时，要考虑不同的拉压模量。

2)通过以上的模拟结果可以充分表明土工格室在抑制路堤的沉降和侧向位移具有显著效果，并且能使上部荷载均匀的向下扩散，提高地基承载力。

3)在土工格室进行模拟时，实体模拟对于沉降和竖向应力影响较大，对于横向位移和横向应力两种方法基本结果相同。

[1]蔡来生，俞焕然.拉压模量不同弹性物质的本构[J].西安科技大学学报，2009，1(1):17-21.

[2]G.Madhavi Latha，K.Rajagopal.Parametric finite element analyses of geocell supported embankments[J].Can.Geotech，2007，44(10):917-927.

[3]张海新，孟昭辉，黄明利.土工格栅改善新旧路面特性的数值模拟[J].基础与结构工程，2010，1(28):124-128.

[4]余 洁，刘云贺，秦 浩.土工织物加筋软土路堤的位移影响分析[J].水利与建筑工程学报，2009，7(2):22-25.