低成本无人机姿态测量系统研究
杨淑洁,曾庆双,伊国兴
(哈尔滨工业大学空间控制与惯性技术研究中心,黑龙江哈尔滨 150001)
0 引言
四旋翼微小飞行器的能量和带载荷能力有限,要求姿态测量系统体积小、质量轻、功耗低。随着MEMS惯性传感器和嵌入式系统的发展,使得研制满足这种要求的姿态测量系统成为可能[1]。但由于MEMS陀螺的噪声和零漂相对于传统的高精度传感器要大很多,单独使用无法满足控制系统的精度要求。本文采用磁场、重力场测量的观测量修正陀螺姿态解算的误差,利用扩展Kalman滤波技术,对不同类型传感器的数据进行数据融合,得到无人机动态的姿态信息。该算法综合了陀螺的短时精度高、加速度/磁强计系统静态精度高的优点,实现低代价较高精度的姿态确定系统。设计的姿态测量精度要求:横滚角与俯仰角的静态输出误差小于1°;航向角的静态输出误差小于2°;航向角的动态输出误差小于3°。
1 捷联惯导系统中载体姿态的确定
捷联惯导系统中,陀螺和加表直接固联在运载体上,设有载体的机体轴确定的坐标系为b,惯导系统采用的导航坐标系为n,b系和n系都是直角坐标系,载体的姿态则是b系和n系直接的方位关系。姿态信息的捷联解算在n系中完成,因此,首先要将固联在载体上的传感器测得的姿态参考向量转换为n系下,这个转换由b系到n系的坐标变换矩阵完成,就是捷联矩阵,根据矩阵中的元素可以求取载体的姿态角[2]。
求取姿态角之前要定义机体坐标系和导航坐标系。本文的导航坐标系定义为东北天坐标系,原点选在无人机重心;机体坐标系原点选在无人机重心,xb沿机体横轴指向右,yb沿机体纵轴指向前,zb沿机体的竖轴指向上,满足右手定则。ψ,θ,φ分别为无人机的航向角,俯仰角和横滚角,则由载体坐标系到导航坐标系转换的姿态矩阵[3]为

在捷联惯性导航系统中常用四元数法完成姿态解算。四元数法算法简单、易于操作,而且可以避免欧拉角的奇异问题,是较实用的工程方法。设Q=q0+q1i+q2j+q3k为n系到b系的旋转四元数,则姿态矩阵与姿态四元数的关系为


2 无人机姿态更新算法
由上文的分析可以看出:表征n系到b系的旋转四元数Q包含了所有的姿态信息,由Q计算出姿态矩阵Cnb,从而确定载体的3个姿态角,因此,姿态解算实质上是计算四元数Q。
根据捷联惯导系统的四元数理论

求解式(3)的微分方程即是对四元数Q进行更新。求解微分方程需要Q的初始值,开机后系统需要静止几秒钟,利用重力场和磁场进行初始对准。
本文的姿态解算系统有2种工作模式。当载体静止或匀速运动的时候,利用扩展Kalman滤波算法来求取姿态信息和更新姿态矩阵[4],同时每周期检测载体的运动状态,当系统检测到载体在进行加速或减速运动时,就在上周期加速度计解算值的基础上,利用陀螺继续解算,如果系统恢复匀速,就重新利用扩展Kalman滤波算法解算。测量系统的框图见图1。
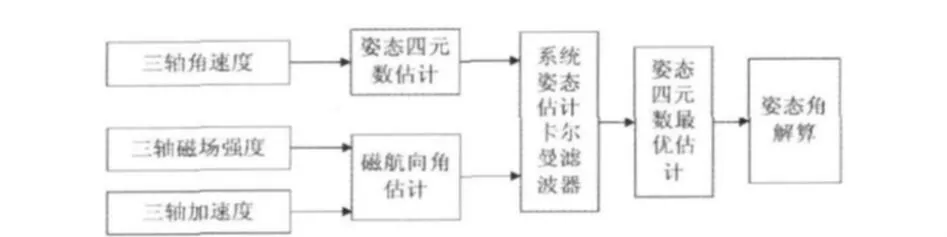
图1 测量系统框图Fig 1 Block diagram of measuring system
判断载体是否处于匀速运动状态,利用加速度计三轴分量与重力加速度的关系来判定。在静止或匀速运动的情况下,加速度计测得的值的平方和应该等于重力加速度的平方值

但在实际系统中由于加速度计的精度和噪声问题,在判断时不可能严格满足式(5),而需要设置一个门限值σ,只要加速度计三轴测得的值的平方和与重力加速度平方值的差小于该门限值,则可视为满足式(5)。
2.1 陀螺动态姿态解算
本文中使用的MEMS陀螺误差较大,并不能敏感到地球的旋转角速度,在算法设计中仅将陀螺仪的输出误差看成常值零偏与白噪声之和,不考虑地球自转。常值零偏在数据初始化时补偿,式(3)中的直接由MEMS陀螺测量输出去除零偏后获得
此处采用四阶龙格库塔法直接求解微分方程˙Q=ΩbQ
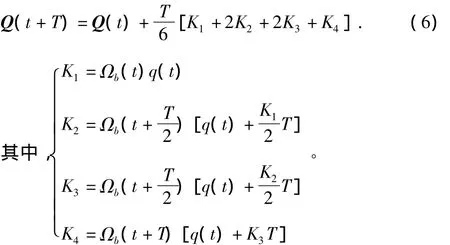
2.2 扩展Kalman滤波姿态解算
采用扩展Kalman滤波器进行多传感器信息融合,就是利用无时间累加误差的重力场和磁场观测量修正陀螺给出的姿态角[5]。
当载体在导航坐标系中静止时,并忽略磁偏角,重力场和磁场在导航坐标系中的投影分别是an=[0 0g]'和mn=[mx0my0mz0]'为已知常量,其中,g为重力加速度。当载体处于任意姿态时,重力场和磁场在集团坐标系中的投影为ab=[axayaz]'和mb=[mxmymz]。
首先构造出一种适合本系统使用的Kalman滤波器模型,采集陀螺仪的数据通过四元数算法得到一组姿态角,将四元数的4个参数做为状态变量

由式(3)得

由式(8)建立Kalman滤波的状态方程

W(t)=[δxδyδz]'近似为零均值高斯白噪声过程,其协方差矩阵Q(t)为非负定常值对角阵。
将方程(9)线性近似离散化,同时忽略高阶小量得到

其中


接着建立观测方程,取观测量为


其中,θ1与φ1为通过一步预测后得到的俯仰角与横滚角。
根据坐标变换关系得到
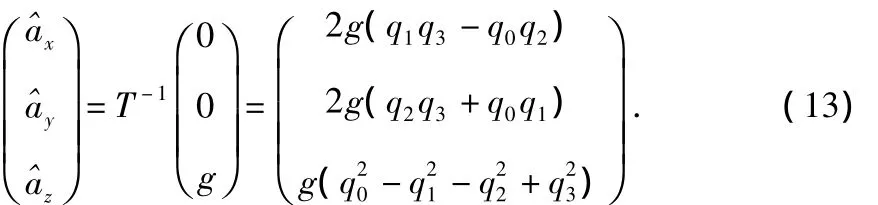
得到观测方程为

其中,V为量测噪声。
线性近似离散化后得到

忽略高阶小量,得到系统量测矩阵H(k)

通过上述的分析,已经得到针对本系统的状态方程与观测方程。根据扩展 Kalman滤波递推方程[7],建立Kalman滤波的时间传播方程。
状态一步预测

均方误差一步预测

状态估计

测量修正方程

3 仿真和实验结果
本文讨论的姿态测量系统的硬件组成包括:MIMU(包括三轴MEMS陀螺和三轴MEMS加速度计)、三轴磁强计和导航计算机,利用MIMU和磁强计感知无人机的运动,传感器信号送至导航计算机,进入姿态解算工作程序。为了验证姿态解算算法的有效性,本文进行了3个实验。在利用实验室现有的三轴转台实验时,由于磁强计易受金属台体的磁场影响,在转台上进行实验时,采用转台的姿态角信号进行信息融合,横滚角和俯仰角保持为零,只能利用偏航角进行比较。
图2的结果是将姿态测量系统置于零位,未采用扩展Kalman滤波器,只利用MEMS陀螺输出计算出的3个姿态角,经过80 s的测试,由于陀螺漂移的存在,可以看出:3个姿态角是发散的。图3的结果是将横滚角和俯仰角保持为0°,将偏航角转至3.5°,并处于静止状态测试60s,3 个姿态角保持在初始值,3个姿态角的误差均小于0.35°。图4的结果是将横滚角和俯仰角保持为0°,将转台偏航角设置为0.25 Hz的正弦信号,扩展Kalman滤波器解算出的偏航角能够很好地跟随转台信号,动态误差小于3°,满足设计要求。
4 结论
本文介绍了一种适合微小型无人机使用的姿态测量系统,将MIMU和磁强计的传感器信号采用扩展Kalman滤波进行信息融合,很好地抑制了MEMS陀螺的漂移。实验表明:3个姿态角的静态误差小于0.5°,航向角的动态误差小于3°,静态、动态精度都能满足无人机对姿态精度的要求。该系统具有成本低、质量轻、体积小的优点。
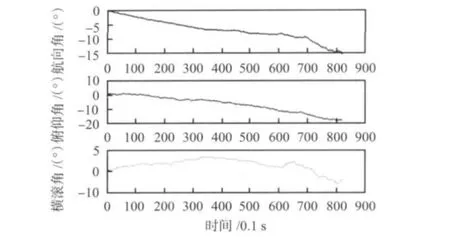
图2 陀螺姿态解算Fig 2 Gyro attitude solution

图3 Kalman滤波静态姿态角输出Fig 3 Attitude angle static output with Kalman filter

图4 Kalman滤波动态姿态角输出Fig 4 Attitude angle dynamic output with Kalman filter
[1]朱 荣.周兆英.基于MENS的姿态测量系统[J].测控技术,2002,21(10):6 -8.
[2]陈 哲.捷联惯导系统原理[M].北京:宇航出版社,1996:82-85.
[3]秦永元.惯性导航[M].北京:科学出版社,2006:297.
[4]黄丽斌,周百令.低成本MINS/GPS组合导航中卡尔曼滤波算法的综合应用研究[J].中国惯性技术学报,2005,13(5):16-19.
[5]Gao Z Y,Niu X J,Guo M F.Quaternion-based Kalman filter for micro-machined strapdown attitude heading reference system[J].Chinese Journal of Aeronautics,2002,15(3):171 -175.
[6]Caruso M J.Applications of magnetoresistive sensors in navigation system[J].Transactions of SAE,1997,106(1):1092 -1098.
[7]秦永元,张洪钱,汪叔华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社,1998:283-286.

