MEMS传感器随机误差分析*

于丽杰，高宗余

（北京联合大学自动化学院，北京 100101）

0 引言

惯性导航系统（INS）能够高速地输出加速度和角速度。然而其精度会随着时间而退化，主要是由于不同的误差源，如，传感器噪声、漂移、偏差及刻度因子等的不稳定造成。这些误差随着在惯导校正算法中数据积分的积累，将会引起航向误差。因此，对传感器误差的建模与估计变得异常重要。本文主要讨论随机误差建模，采用功率谱密度（PSD）与Allan方差对MEMS-INS随机过程进行分析。

Allan方差技术最初是为了研究精密仪器的频率稳定性而在19世纪60年代发展产生的［1］，它有助于识别存在于测量仪器中的误差种类与大小。由于惯性传感器与这类仪器的类似性，这一方法已经应用于惯性传感器的随机误差特性分析中［2］。

与其他的随机误差分析方法相比，如，自相关分析法需要长时间采集精密仪器静态数据，之后在一定条件下才能获得所需结果［3］，采集时间甚至超过仪器寿命，Allan方差法可直接实时进行计算，计算简单，应用范围较大。

本文应用Allan方差法对MEMS传感器进行特性描述。首先对数据采用Allan方差法获得其特性曲线，此后通过对曲线分析以获得存在于数据集中的随机误差的种类和大小，最后对随机误差进行识别、建模、计算出其系数。

1方法

1.1 功率谱密度

功率谱密度（PSD）的主要特点在于描述时间序列的频谱特性，是一种分析数据和表示数据特性的方法，同时对随机误差模型的建立有重要作用。通过对一系列样本的自相关函数估值进行傅立叶变换可计算其相应的PSD。PSD和信号的自相关函数是通过傅立叶变换进行转换，如下式所示

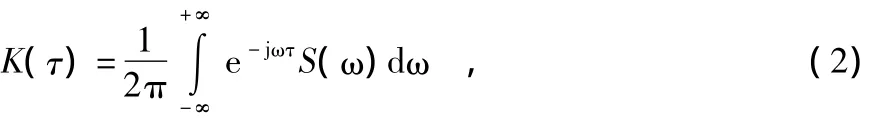
式中S（ω）为PSD，K（τ）为自相关函数。

1.2 Allan方差

在Allan方差数据分析中，假设数据的不确定性是由误差特性给出。每个误差源协方差的大小是由数据估值得来。Allan方差的详细描述和怎样应用于时频分析见参考文献［2，4］。这里做简要描述。假设在时间段τ0内采集N个样本点构成数据点集，分别建立时间段为τ0，2τ0，…，nτ0，的数据点集，n＜（N－1）/2。假设 MEMS传感器瞬时输出为Ω（t），其相应的积分是角度（对陀螺输出来说），如下式

由于在相关定义中［1］只是应用了角微分，故积分的下限没有标出。传感器的角以离散的方式t=kτ0，k=1，2，…，N给出，用更简单的方式表示为

两个时间间隔之间的平均角速率为

Allan方差为

上面的表达式称之为Allan方差重叠法，能更好地适用于每个陀螺和加速度计。

1.3 PSD与Allan方差之间的关系

下式为PSD与Allan方差之间关系表达式

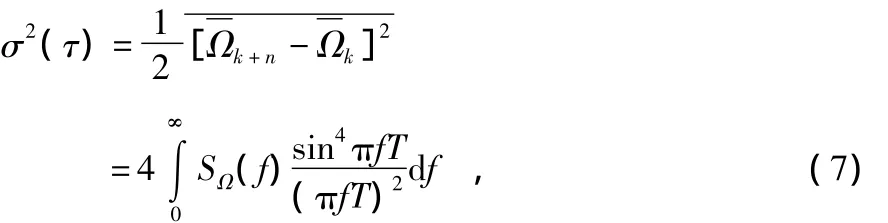
式中SΩ（f）为Ω（t）的PSD。式（7）通过Allan方差方程描述了随机噪声PSD的重要特性。并且说明在通过一个传递函数为sin4x/x2的滤波器时Allan方差与陀螺数据输出中的总的误差率呈正比。这一传递函数主要用于对点集进行操作。式（7）也说明滤波器的带通是由τ来确定，因此，通过设定不同的τ值能够确定不同的随机过程。这里采用重对数图来描述σ［4］。

1.4 Allan方差应用于误差特性描述

Allan方差最主要的特性是能够根据时频域上不同噪声在Allan方差图上的斜率对噪声进行分类。根据Allan方差的定义和结果在惯性传感器中共有七类噪声项，如图1所示。具体到MEMS传感器中共有5类基本的噪声项，分别是角随机游走、速率随机游走、偏差不稳定性、量化噪声和速率斜坡。由于相关噪声和正弦噪声对传感器特性影响很小，因此，对其忽略。通常，随机误差依赖于设备类型、数据获得环境及数据形式产生。如果噪声是相对对立的，则每个Allan方差是各个噪声源的平方和，即

开方后为

其中，An可通过最小均方误差检测得到。

一个典型的Allan方差分析结果如图1所示。然而，由于曲线的类似性，一些误差无法通过特性曲线辨识，比如:闪烁噪声就与量化噪声有同样的曲线图，这主要是Allan方差法受限所致。因此，这类误差需要通过改良的Allan方差法来进行分类［5］。

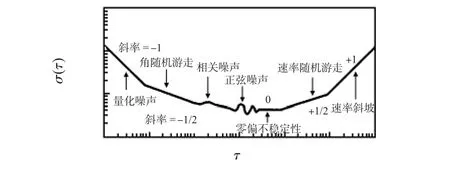
图1 Allan方差类型图Fig 1 Allan variance type map

2 实验仿真

本文中实验平台为MEMS-INS/GPS组合，其主要器件为ADIS16350和GPS系统，本实验主要对ADS16350中的三轴陀螺和三轴加速度计进行实验，其中，ADIS16350传感器特性参数参看文献［6］。

这里以量化噪声为例进行推导。量化噪声主要由传感器输出特性的离散化造成，量化噪声在振幅离散化过程中是固有的，它是通过数字化编码引入模拟信号，是模拟输入到数字输出取整而产生。根据文献［1］这一过程的PSD为

即

上式代入式（7）积分并开方得

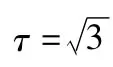
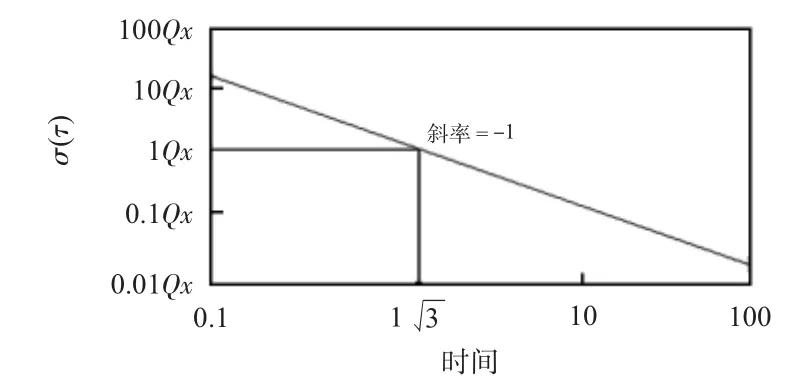
图2 Allan方差系数（以斜率为－1为曲线表示）Fig 2 Allan variance coefficient（result with slopes of－1）

由于篇幅所限，这里不对偏差不稳定性、随机游走及速率斜坡进行具体推导。根据公式（5）首先对加速度和角速度进行积分得到速度和角度。根据上述Allan方差法得到不同时段相应的平均加速度和角速率。最后通过σ（τ）-τ的重对数图来表示陀螺和加速度计的随机噪声的实验结果，分别如图3和图4所示。这里先对图3中陀螺x轴量化噪声系数计算给出具体说明，如图5所示（此实验结果陀螺x轴在4 h所测数据）。

图3 MEMS陀螺Allan方差结果Fig 3 MEMS Gyro Allan variance results

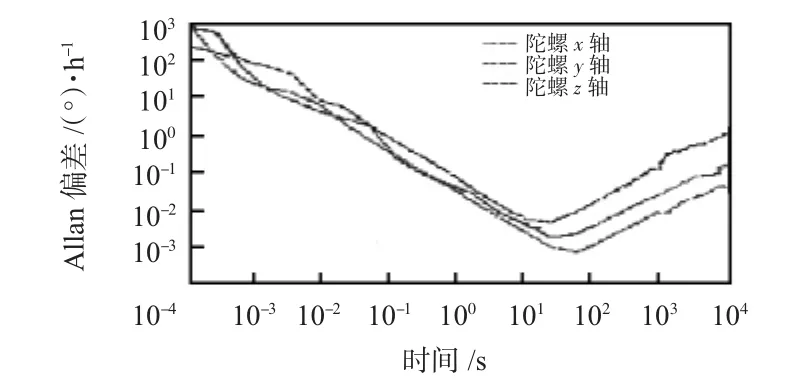
图4 MEMS加速度Allan方差结果Fig 4 MEMS Accelerometer Allan variance results

图5 x轴陀螺Allan方差结果Fig 5 x-axis gyro Allan variance result

表1 陀螺辨识误差系数Tab 1 Gyro identification error coefficients

表2 加速度计的辨识误差系数Tab 2 Accelerometer identification error coefficients

3 结论

利用Allan方差分析法对MEMS传感器输出数据进行分析，能够有效地分离各主要随机误差源，可精确地确定各项误差系数的大小。应用Allan方差分析法对实测数据研究表明:该方法有效辨识出MEMS传感器各项误差系数，从而对MEMS传感器的性能做出较为客观的评价，并且可与滤波算法相结合更好地为微惯性系统性能改善提供好的方法。

此外，这里的实验中注意到数据采集时间越长其计算越精确，但随着时间的增长其数据不稳定性也越高，这主要是MEMS传感器随着数据输出时间的延长其温度发生变化，导致输出数据不稳定所致。

［1］Allan D W.Statistics of atomic frequency standards［C］//Proceedings of the IEEE International Symposium，New York，USA，1966:221－230.

［2］Ko R.Standard specification format guide and test procedure for single-axis interferometric fiber optic gyros［S］.IEEE Std，Canada，1972:952 －977.

［3］Hou H.Modeling inertial sensors errors using AV［D］.Calgary，Canada:Univ of Calgary，2004:182 －188.

［4］Wang J H，Gao Y.An intelligent MEMS IMU-based land vehicle navigation system enhanced by dynamics knowledge［C］//Proc of US ION 61st Ann Meeting，2005:27 －29.

［5］Mu Y J，Ko Jaepyung.An inexpensive and accurate absolute position sensor for driving assistance［J］.IEEE Transactions on Instrumentation and Measurement，2008，57（4）:864 －873.

［6］Papoulis A.Probability，random variables，and stochastic process［M］3rd ed.McGraw-Hill，1977:212 －224.

［7］Lee G W.UAV flight test of GPS attitude determination system［C］//International Symposium on GNSS/GPS，Camb，2004:138－151.