基于相机标定的非对称裁剪检测算法

孟宪哲 牛少彰* 吴小媚 李叶舟

①(北京邮电大学计算机学院 北京 100876)

②(北京邮电大学理学院 北京 100876)

1 引言

随着数码相机的普及以及数字图像处理软件的傻瓜化，针对数字图像的篡改行为日渐增多，这使得数字图像面临着严重的信任危机。数字图像的篡改易于实现，同时难以分辨，又可能引起严重的负面影响，因此针对数字图像篡改的取证技术应运而生。目前，数字图像篡改取证技术的研究主要集中在对图像真实性的取证方面，目前比较完善的取证技术有针对图像复制-粘贴篡改[1]，模糊[2]等具体篡改操作的检测技术体系，以及针对图像的光源[3]特征，重采样[4]特征，彩色图像插值[5]特征，JPEG图像压缩[6]特征等统计特性的检测技术体系。目前，国际上处于领先的研究团队正在推动基于数字图像“弹道”的图像来源认证[7]、图像拍摄时间推断[8]，基于图像文件格式的篡改鉴定[9]等方向的研究。然而数字图像作为信息的载体，真实性只是衡量信息可靠程度的属性之一，数字图像的完整性也应该受到足够的重视。信息的真实性是以完整性为前提的，对图像的断章取义，不会影响截取部分图像的真实性，但是这种以点代面，以偏概全的手段同样是对信息的破坏，甚至在特定的情况下，能使图像传达相反的信息。

对图像裁剪篡改是对图像完整性的最直接破坏手段，通过我们收集的文献来看，目前的取证方法中也有算法能够间接地指证图像中的裁剪篡改，例如现有针对多重 JPEG压缩的检测技术[6]，当检测到图像经过了多次JPEG压缩并且多次JPEG压缩的 DCT变换分块不重叠时，也可以说明图像经历了多次JPEG压缩，由于存在JPEG压缩分块不对齐的情况，可以间接证明图像经历过裁剪篡改，但是该方法仅对多次JPEG压缩的DCT分块不重叠时有效，并且受制于图像保存的质量因子，当末次压缩的质量因子高于首次压缩时，检测算法也会失效；又例如基于相机噪声模式的相机来源认证技术[7]，当检测图像和与之对应的相机噪声模式不匹配，并且部分相机特征点(如像素坏点)缺失的情况下，也可以说明图像经历了裁剪篡改，但是该方法仅适用于已知与图像对应的相机模型的情况，并且要求有一定量的图像用于训练。这些算法虽然在特定的条件下能够从侧面指证图像经历了裁剪操作，但是使用范围比较有限，也无法还原裁剪行为，所以，这些算法不能称之为有效地裁剪篡改检测算法。

本文提出的算法是基于计算机视觉的检测技术，数字成像设备采集到的图像，要满足计算机视觉特征，我们认为截取的图像中的内容没有经过篡改，因此保留了相机的成像规律，由截取的图像估计得到的相机参数将与理论值存在一定的差异，这一差异就可以用做图像经历裁剪的依据，我们通过借助不同平面上的规则图形来估计图像的主点坐标，当主点坐标偏离图像中心时，图像就可能经历了裁剪篡改。

在第2节，我们将简单介绍相机成像模型；在第3节，将介绍应用相机标定方法对图像进行裁剪检测的思想；在第4节，通过实验确定方法的参数和阈值；第5节为结束语。

2 背景知识

一般的数码相机是以CCD传感器为感光元件的，因此都属于有限摄像机模型的范畴[10]。有限摄像机模型的一个基础模型就是针孔模型，针孔模型可以看作一个从3维欧式空间到2维欧式空间的映射：物体首先从一个任意的3维的世界坐标系通过一次外部刚体变换转换到以相机为原点的3维相机坐标系，再经过一次投影变换。物体从3维相机坐标系变换到2维图像坐标系并形成图像，变换过程如式(1)所示。

其中x代表2维图像坐标系中的点；λ代表变换的刻度；K代表3×3阶的投影矩阵，K也叫做相机内部参数，(u,v)是相机主点坐标(对于正常图像，主点坐标就是图像中心的坐标)，α和β分别是相机在图像坐标轴u和v方向上的刻度参数，γ是描述相机CCD与对应图像坐标的歪斜程度的参数；XC代表3维相机坐标系中的点；R代表3×4阶的刚体变换矩阵，R也叫做相机外部参数；XW代表3维世界坐标系中的点。

为了方便计算，在进行对应点选取时，往往选取3维世界坐标系中位于同一平面的点，这样模型可以进一步简化，相机的外部参数矩阵R可以降为3×3阶，并且有

其中H为3 × 3阶的单应矩阵，是后续计算中一个重要过渡矩阵。

3 裁剪检测

由于目前主流的数字图像采集攻击都属于有限摄像机模型的范畴，所以数字图像中的物体满足计算机视觉特征。主点是相机内部参数的重要组成，也是计算机视觉特征中的一个重要元素，主点的物理意义就是相机主视线与透视面的交点，在一幅正常的图像中，主点的位置应该与图像的中心重合。

本文提出的算法就是借鉴主点坐标与图像中心的关系，实现对图像进行裁剪检测的。如图1所示，图像裁剪前后主点坐标与标定物之间的相对关系保持不变，一幅完整图像的主点坐标在图像的中心区域附近，而裁剪过的图像主点则可能偏离图像的中心区域。

图1 图像裁剪与主点关系

目前估计主点坐标一般是借助相机标定的方法，文献[11]提出了基于象棋棋盘的相机标定技术之后，相机标定的方法趋于固定，通过测量图像中的标定物的坐标及其实际尺寸(或者模型尺寸)，根据式(2)来估计单应矩阵H，再借助内部参数矩阵K的形式约束条件以及外部参数矩阵R的正交性约束条件，就能估计主点坐标。

文献[12]将相机标定的方法引入了图像取证，并结合图像取证的特点，对相机标定进行了改进，提出了通过估计主点坐标来实现图像中的拼接篡改的检测，其相机标定的基本思路与文献[11]中的方法类似，其改进在于：

对图像中的标定物体(如人眼、文字等)的建模，通过借助图像中已建模的标定物，摆脱了相机标定必须对标定物进行实际尺寸测量的限制，另外文献[12]采用了期望最大(EM)迭代的方法，降低了因为图像中的点选取不准造成的误差；

对相机的建模和简化，通过简化相机内部参数矩阵，实现通过单幅图像对主点坐标的估计，虽然假设条件过于理想，但是这一尝试更加适合图像取证。

3.1改进的主点坐标估计方法

文献[11]中提到的相机标定方法虽然能够精确地估计相机内部参数，但是需要图像中包含标定板(象棋棋盘等)，同时还需要多幅不同角度拍摄的图像，这对于图像取证显然是无法实现的，因此需要采用类似文献[12]中的方法，对主点估计方法进行简化。

观察式(1)可以发现，内部参数矩阵中一共有5个待定参数，对于目前的主流相机而言，其中α和β的取值相等，并且γ取值可以视为0，那么原先K中的5个参数就减少到3个，因此K可以表示为

令H=[h1,h2,h3],R=[r1,r2,t]，那么式(2)可以表示为

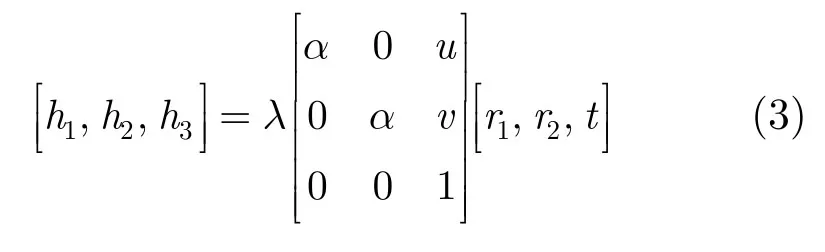
根据文献[11]可知，由于外部旋转矩阵为刚体变

当标定物确定之后，可以借助文献[11]中的方法，得到单应矩阵H的估计，所以式(4)，式(5)就转化为a,u,v为未知数的三元二次方程，由此看出每一组单应矩阵都对应两个约束条件，对于三元二次方程组，仅有两个约束条件是无法对方程组求解的。

文献[12]提出的方法假定K中仅主点坐标未知，使待定参数降为2个，这样做虽然能够得到主点位置，但是方法假设相机的焦距/传感器尺寸信息已知，这就决定了方法仅针对特定的相机，限制了方法的适用范围。经典相机标定方法在解决该问题时是通过拍摄多组照片来完成的，但是在图像取证时，由于很难获得同相机拍摄的其他照片，所以要求通过一幅图像完成主点坐标的估计，为解决约束条件过少的问题，实现通过单幅图像估计主点坐标[13,14]，本文借鉴单幅图像的标定方法[13]，从一幅图像中选取多组不共面的标定物，通过同幅图像中的多组标定物实现对主点坐标的估计。

通过前面叙述可知，选定一组标定物后，可以得到一个对应的单应矩阵，并能根据式(4)，式(5)产生两个关于a,u,v的约束条件。当在同一幅图像中选取另外一组标定物时，也可以得到两个约束条件，若两组约束条件线性无关，就能实现对主点坐标的估计。事实上容易证明，当选取的第2组标定物与第1组标定物不共面时，两组约束条件线性无关。

根据成像规律可知，成像过程的第1步就是将物体从世界坐标系变换到相机坐标系，这一过程是一个刚体变换，这一变换反应在成像过程中就是式(1)中的相机外部矩阵R，当两组标定物不共面时，记两组标定物对应的变换矩阵分别为R(1),R(2)，则一定有R(1),R(2)不相关[11]，令R(1)=Rx R(2),Rx为一刚体旋转矩阵。

记H(1),H(2)为由图像中两组标定物得到的单应矩阵，再根据式(2)H=λKR，可知：H(1)=λ(1)·KR(1),H(2)=λ(2)KR(2)，则H(1)=κRxH(2)，其中κ为缩放因子，由于R(1),R(2)不相关，则H(1),H(2)不相关。

由于H(1),H(2)不相关，所以这4个约束条件是不相关的，通过这4个约束条件就能得到主点坐标的估计。

3.2 改进的标定物的选取规则

文献[12]中提出了对人眼进行建模的方法，实现了不测量标定物的前提下对图像进行标定，这一改进对数字图像取证是非常必要的。虽然文献[12]的方法不再需要对标定物进行实际测量，但是其方法仅针对人像，实验证明该方法仅对正面人像，并且瞳孔暴露较大情况才能适用，这些限制使得基于相机标定的取证方法使用范围受到了限制。

在估计主点坐标的过程中，测量标定物的实际尺寸是为了与标定物在图像中的坐标进行匹配，从而估计单应矩阵H，得到单应矩阵之后，再按照相机外部参数矩阵中的正交关系和相等关系建立一组方程组，通过观察这两个关系以及式(4)和式(5)，我们发现，单应矩阵中蕴含的标定物到图像的变换尺度被抵消了，由于本文仅出于图像完整性鉴定要求，目的仅在于主点坐标的估计，不涉及图像的3维重建等工作，所以在进行主点估计时，标定物的变换尺度可以不用估计，这就意味着在选定标定物之后，不需要对标定物的实际尺寸进行测量，只需要使用相对坐标即可。

由于在标定过程中只需要使用相对坐标，因此在标定物选取时，我们可以选择规则图形。在本文中，规则图形是指形状已知，且各边比例已知的简单几何图形(如矩形、圆[15])，形状固定的商品标示，企业标志以及文字[16]等。图2(a)所示图像中包含有一个中国邮政的标志，我们可以互联网搜索得到图2(b)中所示中国邮政标志的电子版本，并以此为参照物，类比对实际物体进行测量，我们只需要对参照物进行测量，将归一化的坐标作为实际物体坐标，这样得到的单应矩阵与实际的单应矩阵只相差一个常数量级，在选取图像中对应的点，建立坐标对后就能够用常见的相机标定方法计算托量纲的单应矩阵，该托量纲的单应矩阵与实际的单应矩阵仅存在一个倍数的差别。

图2 图像中的规则图形

通过对相机标定算法进行改进，我们能够通过单幅图像实现对主点坐标的估计，该方法对图像的要求也降低为图像中包含两个或两个以上规则标定物，改进后的标定物选取方法更加适合图像鉴定工作。

4 实验结果

我们用一台尼康D5100相机拍摄了一组(200张)包含规则图形的训练图像，拍摄的图像包含了室内、室外等多种场景，每幅图像中均包含两个以上形状规则的图形。分别对训练图像使用本文的算法，就能得到本文算法对训练图像的主点坐标估计结果，我们将坐标进行归一化处理后，可以得到图3中的结果。

图 3(a)中所示情况为文献[12]中提出的算法在无附加条件下，通过人眼得到的主点坐标分布情况；图 3(b)中所示的为本文算法通过两个规则标定物得到的主点估计分布。两幅图像都以 0.2为半径，圈定了主点分布的集中区域，通过对比可以看出，由本文提出的算法估计得到的主点坐标更加有效。

为了验证本文算法在不同裁剪比例下的检测精度，我们选取了实验样本中的50幅进行测试，测试中对图像进行临边裁剪，以保持图像的长宽比例，裁剪比例控制在5%到50%(裁剪比例即裁剪掉的像素的比例)，另外为了验证检测的有效性，我们引入一组与裁剪后图像大小相近的正常图像作对比，使用本文算法对样本进行检测，得到了表1所示结果。

通过表1可以看出，当阈值为图像宽度的0.05倍时，当裁剪比例超过15%时，本文算法对裁剪的灵敏度非常高，但伴随的误检率也处在一个相对高的水平，当裁剪比例达到50%时，仍有10%的误检率，算法在0.05阈值时，检测率较高但误检率也较高，检测效果不理想；当阈值为图像宽度的0.10倍时，本文算法对裁剪比例超过20%的裁剪具有较好的检测率，同时本文算法的误检率也降低到4%，所以算法在0.10阈值时具有比较理想的检测效果；当阈值为图像宽度的0.15和0.20时，本文算法对裁剪的灵敏度变得较差，当检测比例分别超过25%和30%时，算法才能有效的对裁剪进行检测，虽然在这两种阈值下误检率都为0，但是检测灵敏度无法满足实际需求，所以不适合实际检测要求。综上，我们选取0.10作为本算法的检测阈值。

图4(a), 4(b)所示为测试图像中的两幅，图4(c)是对图4(a)的裁剪，除正常裁剪之外，图4(c)

图3 主点分布图

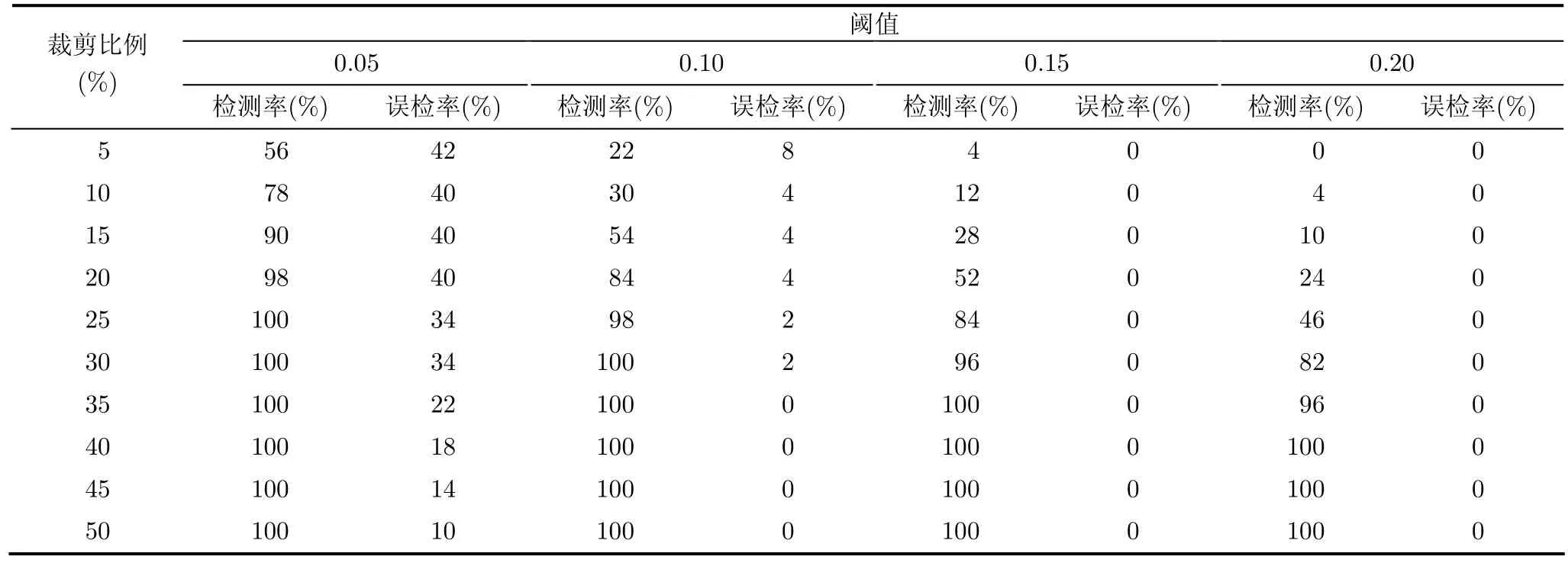
表1 不同阈值下的检测结果

图4 完整性检测示例图像

还对图像进行了轻度的旋转；图4(d)则是将图4(b)中图像一侧拍摄者关心的内容删除，并改变了图像的比例。图4(c), 4(d)中圆点所示位置即使用本文提出的算法计算所得图像主点坐标的位置，可以看出两者都已偏离中心位置，图4(d)的主点更是偏离到图像之外，依据本文算法，两者都被判定为经历了裁剪篡改。

5 结束语

本文提出了一种基于计算机视觉的非对称裁剪检测方法，方法借助相机标定思想，计算图像主点坐标。以往基于相机标定的取证方法需要对真实物体进行建模，同时还对相机有一定的要求，我们通过改进标定模型，在不对相机进行多余假设的条件下，实现了通过单幅图像进行鉴定，另外标定物的选择也不在局限于可建模和测量的物体，标定条件扩展至规则图形，使本文的算法使用范围更加广泛。实验表明，算法对于超过20%的非对称裁剪、图像的截取、以及附带轻微旋转的裁剪具有非常理想的检测效率。在实验过程中我们发现，当图像的裁剪为对称裁剪，即保留部分为原图像中央部分时，本文提出的算法则不能有效地进行检测，另外，当图像经历JPEG压缩并严重影响图像质量时，本文的算法将不再适用，这些都是我们后续的研究方向。

[1]Amerini I, Ballan L, Caldelli R,et al.. A SIFT-based forensic method for copy-move attack detection and transformation recovery[J].IEEE Transactions on Information Forensics and Security, 2011, 6(3): 1099-1110.

[2]Chen Y and Wang Y. Exposing digital forgeries by detecting traces of smoothing [C]. The 9th International Conference for Young Computer Scientists, Hunan, China, 2008: 1440-1445.

[3]Kee E and Farid H. Exposing digital forgeries from 3-D lighting environments[C]. Workshop on Information Forensics and Security, Seattle, WA, 2010: 1-6.

[4]Popescu A C and Farid H. Exposing digital forgeries by detecting traces of re-sampling[J].IEEE Transactions on Signal Processing, 2005, 53(2): 758-767.

[5]Popescu A C and Farid H. Exposing digital forgeries in color filter array interpolated images [J].IEEE Transactions on Signal Process, 2005, 53(10): 3948-3959.

[6]Huang F, Huang J, and Yun Q. Detecting double JPEG compression with the same quantization matrix[J].IEEE Transactions on Information Forensics and Security, 2010,5(4): 848-856.

[7]Fridrich J and Goljan M. Identifying images corrected for lens distortion using sensor fingerprints [C]. Proceedings of SPIE,Electronic Imaging, Media Watermarking, Security, and Forensics XIV, San Francisco, CA, January 2012: 22-26.

[8]Fridrich J and Goljan M. Determining approximate age of digital images using sensor defects[C]. Proceedings of SPIE,Electronic Imaging, Media Watermarking, Security, and Forensics XIII, San Francisco, CA, January 2011: 23-26.

[9]Kee E, Johnson M K, and Farid H. Digital image authentication from JPEG headers[J].IEEE Transactions on Information Forensics and Security, 2011, 6(3): 1066-1075.

[10]Hartley R, Zisserman A, Torr P H S,et al.. Multiple View Geometry in Computer Vision[M]. Robotica, Cambridge Univ Press, 2005: 153-176.

[11]Zhang Z. A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

[12]Johnson M and Farid H. Detecting photographic composites of people[C]. 6th International Workshop on Digital Watermarking, Guangzhou, China, 2007(5041): 19-33.

[13]Huo J, Yang W, and Yang M. A self-calibration technique based on the geometry property of the vanish point[J].Acta Optica Sinca, 2010, 30(2): 465-472.

[14]Liu G, Wang W, Yuan J,et al.. A novel camera calibration method of variable focal length based on single-view[C].International Symposium on Electronic Commerce and Security, Xi’an, China, 2009(2): 125-128.

[15]Hu J, Li Y, Niu S,et al.. Exposing digital image forgeries by detecting inconsistencies in principal point [C]. IEEE the International Conference on Computer Science and Service System, Nanjing, China June 27-29, 2011.

[16]吴小媚, 李叶舟, 牛少彰, 等. 基于相机标定的文字变造篡改鉴定[J]. 北京邮电大学学报, 2012, (已录用，待发表).