正交几何椭圆拟合与代数拟合及椭圆定义的迭代拟合的比较分析

张彦军

0 引言

数字图像处理，又称为计算机图像处理，是指将图像信号转换成数字信号，并利用计算机对其进行处理的过程。也即图像与图像之间的数学变换，对图像信息进行加工以满足人的视觉心理或者应用需求的行为。

目前，天文学上用于拟合星像边缘获得其几何中心位置的方法并不多，常用的有代数拟合方法[1]和椭圆定义的迭代拟合方法[2]。它们都具备其独特之处，如代数方法，其执行效率很高，但当天文图像边缘检测离散点偏离的比较大（例如大气抖动、小区域的饱和等），其精确度就不够理想。相比之下，椭圆定义的迭代拟合方法就具有很高的精度。因此，本课题的研究目的、意义就是应用边缘提取算法对天文图像的边缘进行提取和处理的同时，考虑到一般拟合算法的缺陷（例如，可能剔除一些正常的边缘点），充分地应用正交的概念及最小二乘（LS）原理和方法的优点，对椭圆进行正交几何拟合，并对这些方法的拟合结果进行比较分析。理论上来说，正交概念可以提高其判断边缘点的标准，对边缘点处理都是公平的，没有进行强制加权，所以正交几何椭圆拟合可以适当的弥补其它拟合算法的缺陷。

1 椭圆拟合相关算法

1.1 代数拟合方法

在文献[1]中对代数拟合方法有详细地描述。假设一般形式的椭圆方程为:

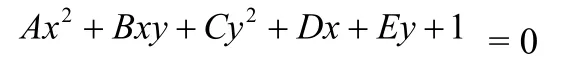
这里, 常数项已经归一化为 1。显然, 直接应用上述方程对边缘检测后的离散点进行最小二乘原理，就可以得到方程中的各系数。也即，对应于求目标函数

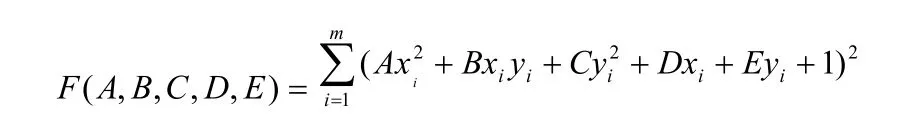
求最小值来确定各系数。再由极值原理，欲使 F 为最小，必有：

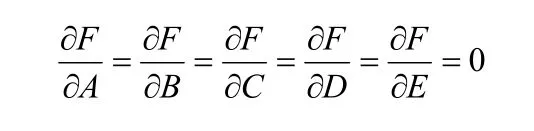
由此可得以下正规方程组,进而应用求解线性方程组的算法（如全主元高斯消去法），就可以得出方程系数A、B、C、D、E的值，从而可导出椭圆各估计参量：椭圆几何中心xcyc,椭圆长轴的倾角θ，椭圆半长轴a和半短轴b.1.2椭圆定义的迭代拟合文献[2]对椭圆定义的迭代拟合方法进行了阐述。在代数拟合方法的基础上，假设椭圆上任一边缘点为P(x,y)，椭圆两焦点位置为F1(x1,y1)和F2(x2,y2)，焦距为 2c.而我们知道，理想椭圆上的点到两焦点距离之和为常数(2a)，实际中，由于不可避免的误差影响，理论上，对所有椭圆边缘的离散点进行最小二乘拟合就可求得椭圆的5个待求参量的估计。

我们可以将代数拟合方法中求得的结果作为初始值,则观测方程应用于所有边缘的离散点进行最小二乘拟合,并逐步迭代可最终获得所有待求参数 （x1,y1;x2,y2;a）。在迭代过程中我们可采用如下准则：

(1) 每次椭圆拟合后剔除残差v的绝对值(σ为每一次迭代拟合后单位权标准误差)的边缘离散点。

(2) 如果相邻两次迭代拟合时每一椭圆焦点位置的偏差绝对值均不大于0. 001 像素,则迭代过程终止。

实际中, 我们可以发现，上述迭代通常只需 3～5次即可收敛。最后, 我们可以得到椭圆中心的测量位置

2 正交几何椭圆拟合算法的原理及其思想

我们已经详细介绍了几种椭圆拟合方法，如代数拟合方法与椭圆定义的迭代拟合方法，但它们都相应地存在一些缺陷，如：代数拟合方法的精度不够理想。而对于椭圆定义的迭代拟合方法，其边缘点可能被不情愿地进行了加权，致使在迭代的过程中，剔除了一些正常的边缘点，从而影响到椭圆中心定位的精度。针对以上问题，将阐述一种严格的、健壮的椭圆几何拟合无参算法 正交几何拟合算法。此算法是基于通过给定点到符合其几何特征的相关点的坐标描述，此时，从给定点到几何特征拟合点之间的连线是最短的。理论上，正交几何拟合方法，充分应用正交的概念和最小二乘原理，克服了以上各方法的缺点，从而期望得到更好的精度与执行效率。

对于正交几何拟合方法，在Ahn等人的文献[3]中有详细描述，在此，对其主要内容做个集中说明。在椭圆的几何拟合中，椭圆的拟合相关点只是通过正交关联条件表示出。当给定点的几何特征相关点显式或隐式得知时，都可以得出在这些点的Jacob矩阵，且可以应用非线性最小二乘迭代方法解之。

2.1 非线性最小二乘拟合

假定待测量a（a1, ...,aq）和观测量X（X1,...Xp）(p≥q)的关系如下：

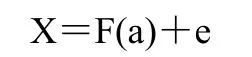
其中，F表示为a的非线性可连续微分的观测函数向量，e表示为零平均值误差向量。X对a的非线性最小二乘估计就必须最小化其性能因子，表示如下：

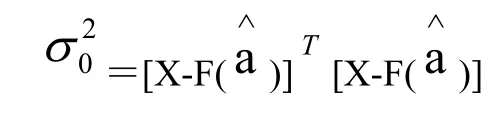
2.2 椭圆的正交几何拟合

对于椭圆，在一个平面上，可以用以下5个参数唯一的表示 它：中心坐标Xc,Yc， 半轴长a,b(a≥b), 和倾角α(-π/2 < α≤π/2)。

由于椭圆存在一旋转角α，在此方法中引入了一个临时坐标系xy，其坐标系旋转角也为α。对于椭圆拟合，引入临时坐标系与正交相'关条件一样，都是为了得到给定点在原来椭圆上相关点Xi的Jacob矩阵。

引入坐标系xy和坐标系XY之间的变换关系表示为：

3 正交几何椭圆拟合、代数拟合及椭圆定义的迭代拟合实例分析比较

在文献[3]中对正交几何拟合算法进行了评估，对于给定的同一组初始值，Gander等人的算法[4]需要经过71次迭代后，精度可以达到 1.1×10-6，而正交几何拟合方法仅需要21次。并且由于圆几何拟合的结果可以作为正并几何拟合的初始值，但不能作为Gander算法的合理初始值。这些充分地说明了正交几何拟合方法的健壮性与稳定性。下面通过将此方法与天文图像定位现有拟合方法（代数拟合方法与椭圆定义的迭代拟合方法）做分析比较，以此来说明此方法的可行性与实用性。为方便起见，取定椭圆上均匀分布的12个点，并假设各参数的预设值为：

其12个点在椭圆上的分布图，如图1所示：

为了能更全面的比较与分析，我们将分以下7种情况进行考虑：

取定椭圆上全部12个点。(如图1)

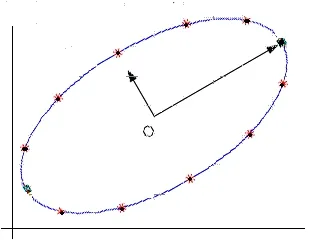
图1 均匀分布12点椭圆

取定椭圆上半部分7个点。(如图2a)

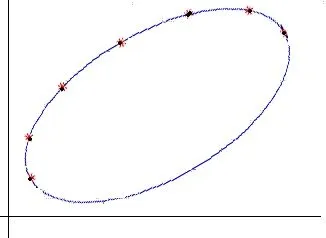
图2a

取定椭圆下半部分7个点。(如图2b)

图2b

取定椭圆左半部分7个点。(如图2c)

图2c

取定椭圆右半部分7个点。(如图2d)

图2d

取定椭圆x轴左右两边附近3点共6个点。(如图2e)

图2e

取定椭圆y轴上下两边附近3点共6个点。(如图2f)

图2f

当取定的是椭圆上点，而未加任何噪声时（也即没有任何偏差的情况），通过实验可以知道，不管是代数拟合方法，椭圆定义的迭代拟合方法，还是正交几何拟合方法，以上各种方法的误差都精确为0，这也符合了理论上的推导。

为了便于比较，下一步就为它们增加噪声，在此选定正态分布的随机噪声。其均差μ=0，方差σ=1.5，且设定噪声范围为（-0.5～0.5）。正态分布的随机噪声可参考文献[6]。

当给这些观测点分别增加随机噪声后，可得到以上 7种情况的实验结果数据表：

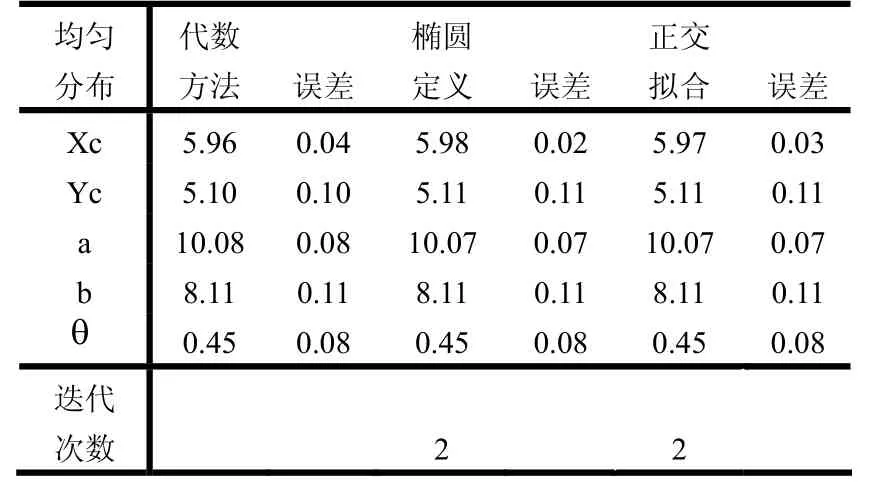
表1 椭圆上均匀分布的12个点

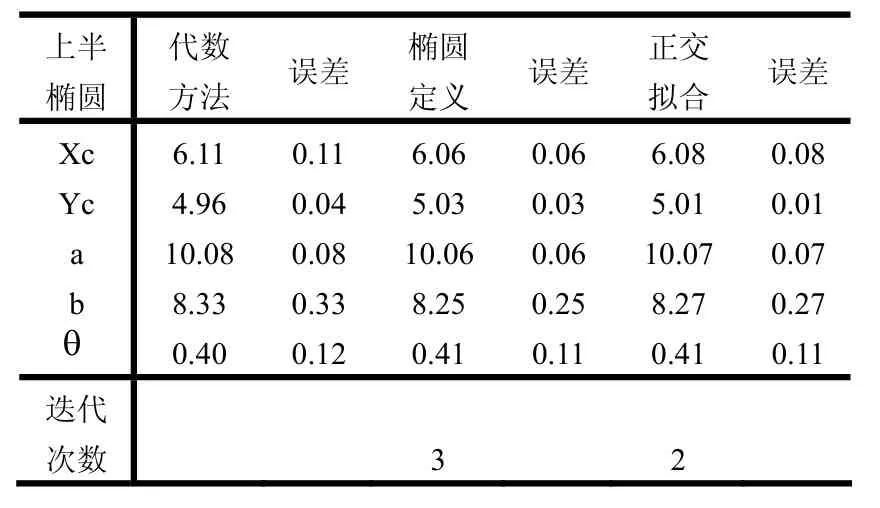
表2 椭圆上半部分的7个点

表3 椭圆下半部分的7个点

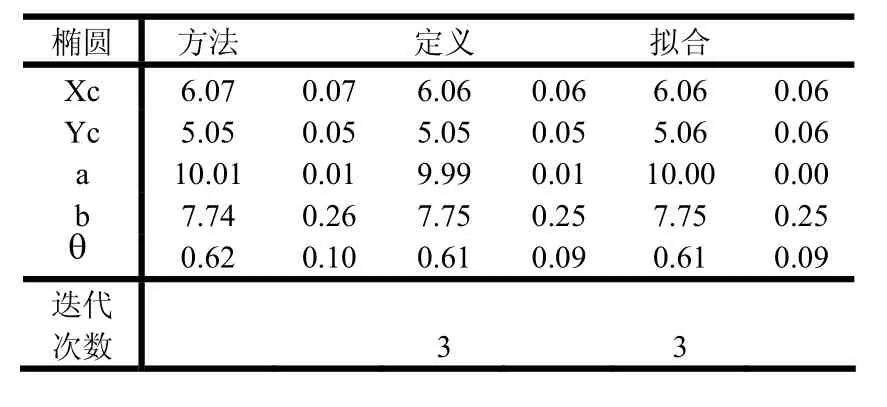
椭圆 方法 定义 拟合Xc 6.07 0.07 6.06 0.06 6.06 0.06 Yc 5.05 0.05 5.05 0.05 5.06 0.06 a 10.01 0.01 9.99 0.01 10.00 0.00 θ 0.62 0.10 0.61 0.09 0.61 0.09 b 7.74 0.26 7.75 0.25 7.75 0.25迭代次数 3 3

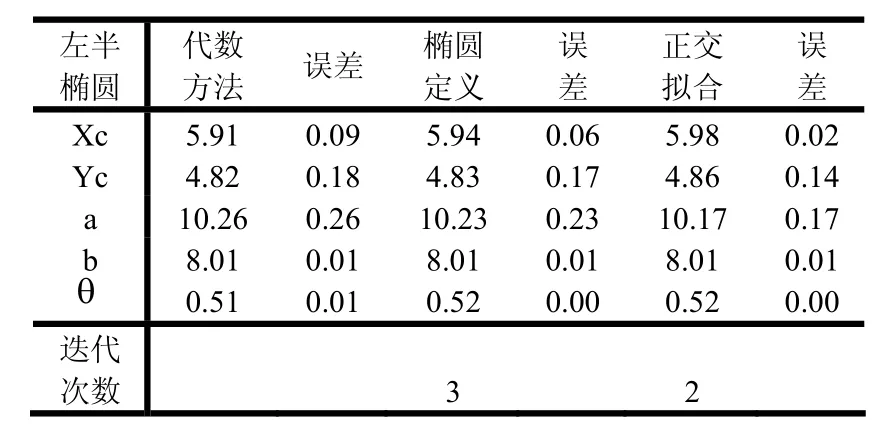
表4 椭圆左半部分的7个点

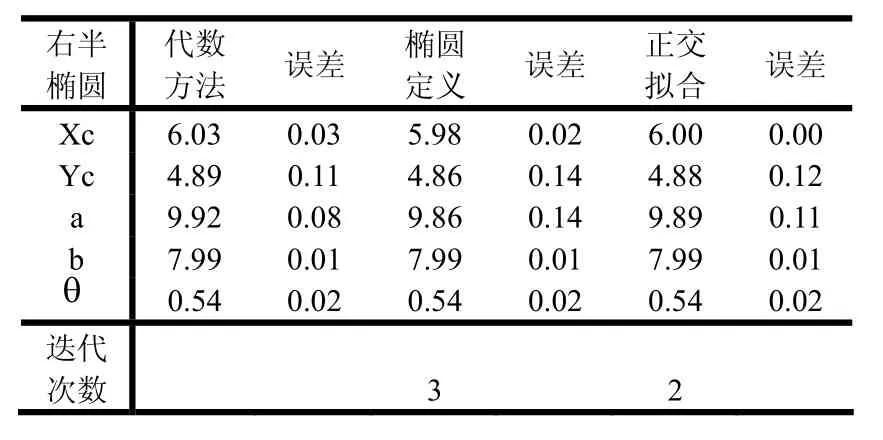
表5 椭圆右半部分的7个点

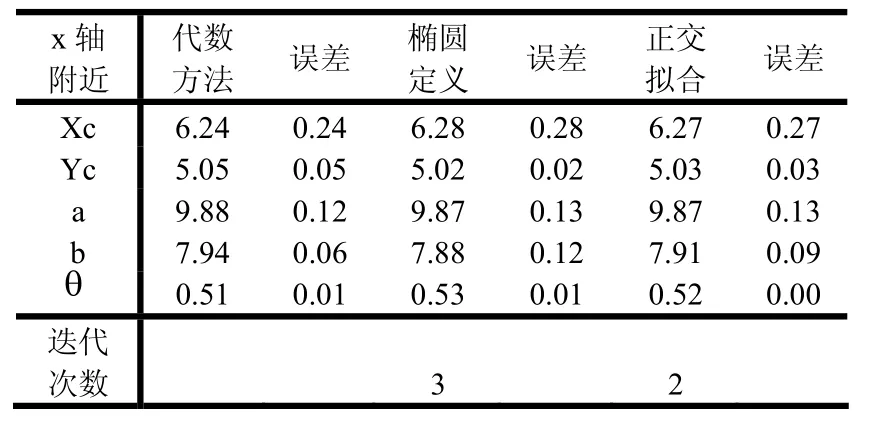
表6 椭圆x轴左右两边附近3点共6个点

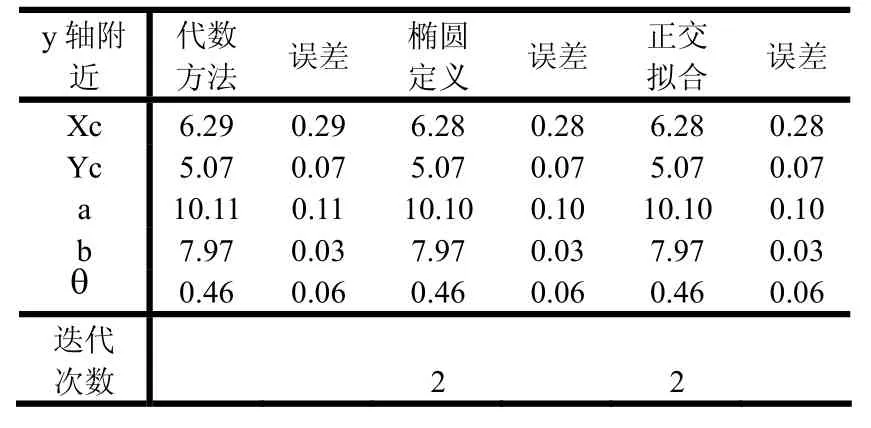
表7 椭圆y轴左右两边附近3点共6个点

其中，由于椭圆定义的迭代拟合和正交几何拟合方法，都是在代数拟合方法基础上进行处理的，将代数拟合的结果作为其迭代的初始值，因此，它们只需要经过不到3次的迭代就可以达到所要求的精度（即相邻两次迭代拟合时每一椭圆焦点位置的偏差绝对值均不大于0.001像素）。通过对上面数据表的比较，可以发现，代数拟合方法、椭圆定义的迭代拟合方法、正交几何拟合方法对椭圆拟合的精度都较好，误差也并不是很大。究其原因，可能是由于所选观测点是均匀分布的，且增加的噪声也是均匀的。但相对来说，正交几何拟合方法的结果更好些，其迭代次数也要少些。因此，可以增加观测点个数、增大随机噪声及增大观测点分布的随机性。取观测点个数n=20，各参数的预设值为a=10，b=8，xc=6，yc=5，θ=π/10≈0.31415，同时增大随机噪声范围为（-2.5～2.5），考虑第6种情况对以上3种方法进行比较。可以得到以下的数据，如表8所示：

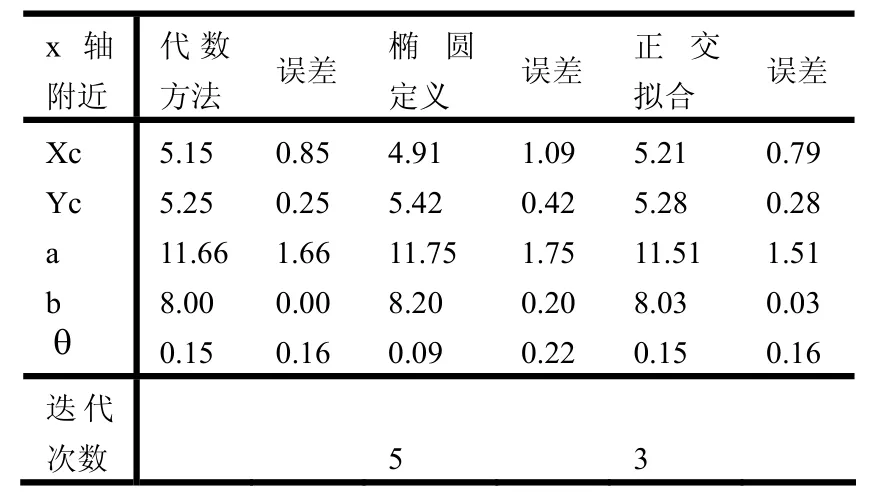
表8 椭圆x轴左右两边附近5点共10个点

从上表中可以发现，相比椭圆定义的迭代拟合，正交几何拟合要理想得多，其迭代次数也更少。而对于代数方法，其结果似乎更理想，但代数方法的思想是一次性定位各参数，从理论上，如果偏差达到一定域值时，其精度肯定是达不到的。当再一次把噪声增大些，如（-5～5）或者更大时，椭圆定义的迭代拟合有时会出现发散的情况，而正交几何拟合方法则不会。因此正交几何拟合方法是非常健壮与稳定的，也是可行的。

5 总结

在一幅天文图像中，存在着大量的信息数据，需要从图像中获取出这些信息数据，并对它们进行处理，因此就要求具有很高的执行效率和精度。所以，就可以放心的将正交几何拟合方法应用到天文图像中去。

[1]Stone R.C., Digital centering algorithms for the sun,moon, and planets,[j]AJ. , 1990, Vol99, No1: 424-430.

[2]彭青玉, 木星土星边缘的椭圆拟合,[j]云南天文台台刊, 2003, No4: 43-48.

[3]Ahn S.J., Rauh W., Warnecke H., et al. Least-square orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola.[j]Pattern Recognition, 2001,Vol34: 2283-2303.

[4]Gander W., Golub G.H., Strebel R., Least-squares fitting of circles and ellipses,[j]BIT, 1994, No34: 558-578.

[5]H., Orthogonal distance fitting by circles and ellipses with given area, Computing.[j]Stat., 1997, No12:343-354.

[6]张圣华编著, 《C语言数值算法》,[M]北京，海洋出版社, 1993-8.