基于差分算法的贴装顺序优化问题求解

朱光宇，罗 哲，陈志锦

（福州大学 机械工程及自动化学院，福建 福州 350002）

当今电子元器件的封装技术迅速向小型化、微型化、片式化、高性能方向发展［1］，而传统通过人工插件组装的方式在印刷电路板（Printed Circuit Board，PCB）上安装元器件的方法已经远远不能适应于当今的要求.由于表面贴装技术（SMT）的先进性，已被广泛使用于工业生产中，而其中的拱架型多头贴片机又由于其适用元器件的范围最广且最具柔性而得到广泛应用［2－4］.拱架型多头贴片机的高效运行已经成为制约该类设备发展的关键所在，而其高效运行又可归结为一种典型的表面贴装工艺优化问题，主要包括供料器位置分配优化、元器件取料顺序优化、元器件贴放顺序优化［5－6］3个子问题，而这些问题均属于NP（Nondeterministic Polynomial）问题，具有高维数、离散和非线性的特点.

众多学者针对表面贴装工艺优化问题开展研究，主要是利用多种智能型优化算法来解决拱架型多头贴片机贴装的优化问题［7－8］，如遗传算法（GA）［9－10］、粒子群算法［11］等.文献［12］在给定元器件取料顺序和贴放顺序的前提下，利用遗传算法解决了供料器分配的优化问题.文献［3］提出了一种以正负数为符号的染色体编码方式的遗传算法对供料器位置分配进行了优化，实验表明该算法取得了有效的优化结果.文献［11］在分析了表面贴装过程调度问题特征的基础上，提出了一种离散粒子群优化算法对供料器位置和取料顺序进行了优化.文献［13］提出了一种以作者名字第一个字母命名的基因遗传算法（LBM-GA）来优化供料器位置分配和元件的取料顺序.文献［14］用神经网络算法来求解元器件贴放顺序的优化问题.此外，元器件贴装顺序优化问题的求解方法还有模拟退火算法［15］等.

虽然文献［3］和文献［12］应用遗传算法或改进的遗传算法在解决贴片机贴装的优化问题中取得了较为满意的结果，但无法摆脱遗传算法本身所具有过早收敛的局限性［16］.鉴于这种情况，本文提出了应用差分算法来解决拱架型多头贴片机取料、贴放的优化问题.差分算法（Differential Evolution，DE）的主要应用领域为函数优化、组合优化、神经网络训练［17］及其他进化算法常用的应用领域.文献［18］和文献［19］应用DE算法在求解旅行商问题、布局优化、图形划分问题等具有NP难度的问题上获得了成功.因此，将DE算法应用于SMT的贴装顺序优化问题具有十分广阔的前景.本文针对上述情况，以贴片机取料、贴放时间为研究对象，建立了以取料、贴放总时间为优化目标的数学模型，对DE进行改造，使其适应于表面贴装工艺优化问题，并进一步改进差分算法，建立带迁徙操作的差分算法（Differential Evolution with Migration，MDE）.通过实验选择DE算分的参数，将DE，MDE，GA算法进行比较.

1 PCB取、贴顺序描述及数学模型

1.1 问题描述

拱架型多头贴片机主要由放置PCB的工作台、供料槽、供料器、贴片头、吸嘴等组成，其结构如图1所示.贴片机表面贴装优化中的贴片工艺过程如下［20］：首先，装有元器件的各供料器摆放在贴片机供料槽的不同位置，PCB通过输送带被输送到贴片机并固定下来，贴片头上的吸嘴依次或同时在取料点吸取供料器中的元器件，通过视觉检测后，贴片头移到PCB上的相应位置，依次贴放这些元器件，然后返回取料点再次取料.这样一次取料、贴放操作过程称为一个取、贴循环，如此循环取、贴，直到所有元器件取、贴完毕.通过上述贴片工艺可知，影响贴装效率的主要因素便是贴装元器件的取料、贴放顺序，因此合理地安排贴装元器件的取料、贴放循环顺序，便能够减少贴装过程的总体时间，进而提高贴装效率.

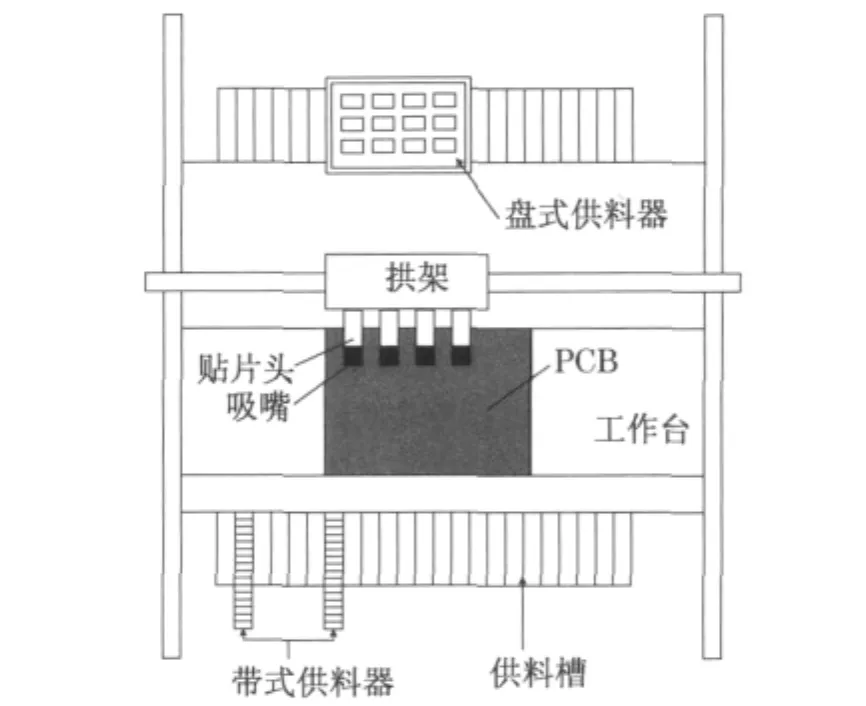
图1 拱架式多头贴片机结构示意图Fig.1 Example of gantry surface mounting machine

1.2 模型建立

通过分析可以看出PCB贴片工艺的优化是一个非常复杂的问题，而且也会增加模型的求解难度.因此，为建立一个合适的数学模型，必须简化一些不必要的环节.本文假设①贴片头的运动为均匀运动；②贴片头每次取料、视觉检查及贴放所耗费的时间为恒定值；③每种元件只对应一种吸嘴.设t1为贴片头每次上下运动完成取料或贴放所耗费的时间；t2（i）为第i次循环中吸嘴更换所需的时间；t3（i）为第i次循环中贴片头在供料器上完成这轮取料移动所用的时间；t4（i）为第i次循环中贴片头从某一取料点移动到PCB，并完成这轮元件贴放过程中移动所用的时间；tij为贴片头从取、贴循环i最后一个贴放点移动到取、贴循环j第一个取料点移动所用的时间；xi，j用于判断取贴循环i，j是否相邻（相邻取1，否者取0）；n为PCB总的元器件数；L为取、贴循环的总次数.则元器件贴装顺序用时间来表示的目标函数及约束条件如下：

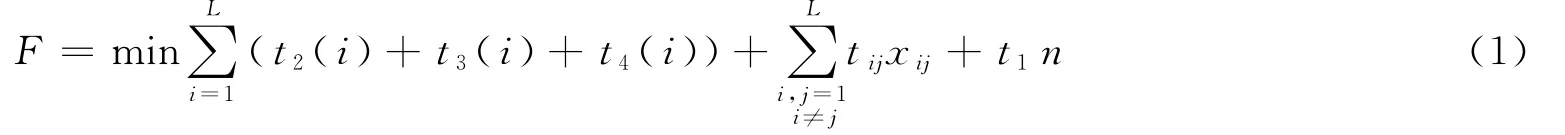
其中：

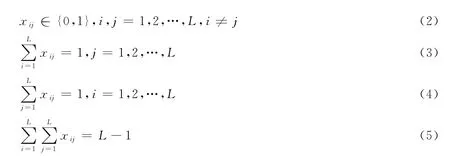
式（2）—（5）保证每个取、贴循环有且仅有一次.

2 DE算法在贴片机取、贴顺序优化中的应用

2.1 解的表现形式

在表面贴装优化中，元器件的取料、贴放顺序是离散的，本文利用元器件编号的顺序编码来表达取、贴顺序，即解的表现形式是取料、贴放顺序的整数编码，每个码位值是PCB上一个元器件的整数编码.

首先对PCB上所有的元器件进行编码，假设一块PCB上共有n个m类型的元件，贴片机有f个供料槽｛s1，s2，…，sf｝，对n个元件依次进行编码：｛1，2，…，n｝，用｛c1，c2，…，cm｝分别表示m种类型的元件，则元件、类型、供料槽的对应关系为：｛1，2，…，n｝→｛c1，c2，…，cm｝→｛s1，s2，…，sf｝，其中m≤f≤n，即每种类型元件（也即装载这种元件的供料器）安放在某个或某几个供料槽上，那么只要知道了要贴装的元件代码i（i∈（1，2，…，n）），通过这种对应关系就可以知道元件的类型以及它所在的供料槽.

例如用拱架型4头贴片机贴装12个元件，有关系如下：

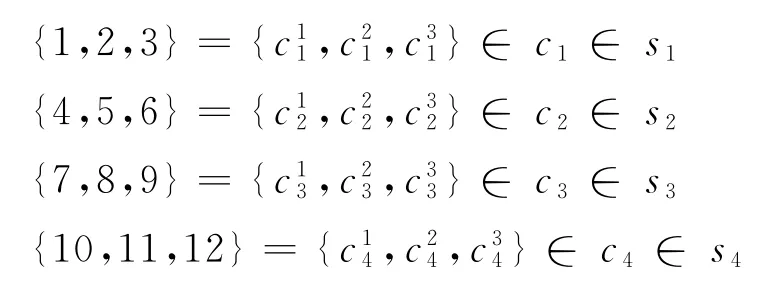
2.2 带迁徙操作的DE算法

DE算法的关键步骤是变异操作，而变异操作是基于群体的差异向量信息来修正各个体的值，随着进化代数的增加，各个体之间的差异化信息在逐渐缩小，导致后期收敛速度变慢，甚至有时会陷入局部最优解.因此，本文在原有DE算法的基础上提出MDE算法，即在算法搜索过程中引入迁徙操作，在保持个体优良性的同时增大了种群的多样性.

迁徙操作的主要思想是：当迭代次数达到总迭代次数τ的1/4时，保留当下目标函数值较好的前半部分群体，作为种群1，然后重新开始迭代，当迭代次数达到总迭代次数τ的1/2时，保留当下目标函数值较好的前半部分群体，作为种群2，综合种群1和种群2，继续迭代下去，直到达到总迭代次数τ，其目的是增加种群多样性，以此来跳出局部最优解，从而得到了更优解.

2.3 算法流程及实现方式

在算法运行前需设定的参数为：种群规模数N，缩放因子η，交叉概率C及进化过程的总迭代次数τ，面向贴装优化问题的MDE算法流程如下：

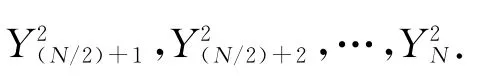
（8）迁徙进化进程3.利用种群3，重复（1）至（4），直至种群3的迭代次数t＝τ时算法终止.

（9）检测算法终止条件t＝τ.若满足终止条件，则转入（10），否则转入（2）.

3 实验分析

本文使用MATLAB软件实现算法，实验以有4个贴片头的拱架型贴片机为试验对象，贴片机槽位总数为80，贴装循环中贴片头的移动速度为v＝1 000mm·s－1，测试的对象为A，B两块PCB，其中A板面积为137mm×91mm，B板面积为230mm×152mm，A板包含6类元件：15个电阻（R）类、11个连接器（U）类、4个集成电路（IC）类、10个三极管（RL）类、5个可控硅（IR）类、15个电容（C）类元件，分配贴片头1取、贴R类，贴片头2取、贴U，IC类，贴片头3取、贴RL，IR类，贴片头4取、贴C类元器件.B板包含7类元件：29个RL类、19个IR类、36个C类、19个IC类、11个电感器（IV）类、12个U类、42个二极管（OR）类元件，分配贴片头1取、贴RL，IR类，贴片头2取、贴RL，C类，贴片头3取、贴IC，IV，U类，贴片头4取、贴OR类元器件，使得各贴片头的负载尽量均衡.

3.1 算法参数对算法的影响

DE算法包含3个参数，本文采用在3个参数中保持2个参数不变、改变另一个参数的情况下对A，B板进行实验，以确定较佳的算法参数.实验中，A，B板的N，η，C作为不变参数时分别设为50，0.5，0.5和75，0.5，0.5，所用的实验迭代次数均为400次，每次实验独立运行20次，实验分为3个过程：①η，C保持不变，参数N分别取25，50，75，100，125，150；②η，N保持不变，参数C分别取0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9；③C，N保持不变，参数η分别取0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9.A，B板按照上述过程20次优化结果平均最优值依次如图2所示.

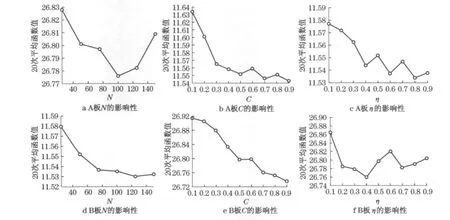
图2 实验A，B板时算法参数对性能的影响Fig.2 Influence of algorithm parameter to performance for testing A and B board.

实验结果表明：①种群N的选择跟优化对象的规模相关，一般来说元器件数量大的优化问题，种群相应增大，能够得到较好的优化结果，但种群大到一定程度后优化结果反而会随种群的增大而减少；②交叉参数C的选择不宜过小，大于0.4的值较好；③缩放因子η选择在0.4～0.8的范围内较好.

3.2 DE，MDE，GA算法的比较

分别将DE，MDE，GA算法采用相同随机初始值，对A，B板的贴装工艺进行优化，各运行20次优化实验，记录下3种算法每次的最优贴装时间并求平均值.DE，MDE算法中，C＝0.7，η＝0.8，最大迭代步数τ＝600；GA算法中，C＝0.5，变异概率为0.08，最大迭代步数τ＝600，实验结果如图3、表1所示.

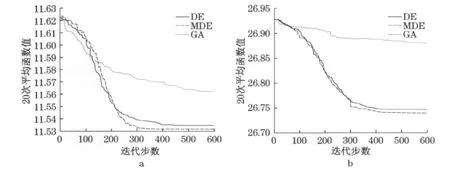
图3 A，B板三种算法20次平均最优值的迭代过程Fig.3 Iteration process of optimal value to 20times′ means for three algorithm of A and B board

表1 三种算法计算结果比较Tab.1 Comparation of results for three algorithm

从图3中可以看出DE，MDE算法的收敛速度明显较GA算法快，在迭代到300步时，由于迁徙操作的使用，MDE平均最优值出现阶跃下降，表明迁徙操作能够显著地使DE算法跳出局部最优解.同时，从表1可知，针对两个不同实验对象，DE，MDE的平均最优值、最佳最优值要好于GA算法的结果.MDE的平均最优值要好于DE的结果，表明迁徙操作使算法有更多机会收敛到最优解.本文所采用的DE算法较GA算法的优化结果要好，优化质量要高，且随着PCB元件数量越多优化结果越好，但由于实验的PCB元器件之间的间距较小，且板面本身面积较小，因此提高的比率较少.

4 结语

本文探讨利用DE算法及其改进后的带迁徙操作的DE算法对贴片机贴装工艺进行优化，解决了拱架型多头贴片机的元器件取、贴优化问题.通过实验表明，DE算法、MDE算法能够有效地解决拱架型多头贴片机元器件的取料、贴放优化问题，优化结果较GA算法明显好.本文所建立的DE算法流程能够满足贴片机取料、贴放顺序优化的需求，而且对其他离散优化问题具有借鉴意义.

［1］王英章.高精高速微孔PCB数控钻床关键技术的研究与应用［D］.重庆：重庆大学，2005.

WANG Yingzhang.Study and application of some key techniques of high accuracy and high speed PCB NC drilling machine［D］.Chongqing：Chongqing University，2005.

［2］AYOBM，KENDALL G.A survey of surface mount device placement machine optimization：machine classification［J］.European Journal of Operational Research，2008，186（3）：893－914.

［3］LI Shaoyuan，HU Chaofang，TIAN Fuhou.Enhancing optimal feeder assignment of the multi-head surface mounting machine using genetic algorithms［J］.Applied Soft Computing，2008，8（1）：522－529.

［4］ELLISS K P，VITES F J，KOBZA J E.Optimizing the performance of a surface mount placement machine［J］.Transactions on Electronice Packaging Manufacturing，2002，24（3）：160－170.

［5］SUNA D S，LEEA T E，KIM K H.Component allocation and feeder arrangement for a dual-gantry multi-head surface mounting placement tool［J］.Production Economics，2005，95：245－264.

［6］ALTINKEMER K，KAZAZ B，KOKSALAN M，et al.Optimization of printed circuit board manufacturing：integrated modeling and algorithms［J］.European Journal of Operational Research，2002，124（2）：409－421.

［7］KUMAR R，SENIOR，LUO Z H.Optimizing the operation sequence of a chip placement machine using TSP model［J］.IEEE Transactions on Electronics Packaging Manufacturing，2003，26（1）：14－21.

［8］KENDALL M A G.Real-time scheduling for multi headed art placement machine［C］∥Proceedings of the IEEE International Symposium on Assembly and Task Planning.Piscataway，New Jersey：IEEE，2003：128－133.

［9］EILLIAM H，PING J I.Component scheduling for chip shooter machines：a hybrid genetic algorithm approach［J］.Computers ＆Operations Research，2003，30（14）：2175－2189.

［10］OONG N S，KHOO L P.Sequence placement planning high-speed PCB assembly machine［J］.Integrated Manufacturing Systems，2002，13（1）：35－46.

［11］伍楷舜，郝井华，刘民，等.表面贴装过程调度问题的粒子群优化算法［J］.控制工程，2007，14（2）：132－139.

WU Kaishun，HAO Jinghua，LIU Min，et al.Particle swarm optimization algorithm for scheduling problem of surface mounting process［J］.Control Engineering of China，2007，14（2）：132－139.

［12］田福厚，李少远.贴片机喂料器分配的优化及其遗传算法求解［J］.控制与决策，2005，20（8）：955－960.

TIAN Fuhou，LI Shaoyuan.Optimization of feeder assignment using genetic algorithms in surface mounting machine［J］.Control and Decision，2005，20（8）：955－960.

［13］TECK S L，SATISH T S B，DEBORAH M，et al.A genetic algorithm for sequential part assignment for PCB assembly［J］.Computer ＆Industrial Engineering，2001，40：293－307.

［14］SU Y Y，SRIHARI K.Placement sequence identification using neural networks in surface mount PCE assembly［J］.International Journal of Advance Manufacturing Technology，1996，11（4）：285－290.

［15］TIPAK T M，NELSON P C，ASWANI A J.Optimization of revolver head SMT machine using adaptive simulated annealing（ASA）［C］∥Twenty-Sixth IEEE/CPMT International，Electronics Manufacturing Technology Symposium.Santa Clara，CA：IEEE Service，2000：214－220.

［16］刘智明，贺新，周激流，等.基于排序的改进自适应遗传算法［J］.信息与控制，2001，33（1）：6－8.

LIU Zhiming，HE Xin，ZHOU Jiliu，et al.Study on improved adaptive genetic algorithm based on ranking［J］.Information and Control，2001，33（1）：6－8.

［17］王雪松，程玉虎.一种基于时间差分算法的神经网络预测控制系统［J］.信息与控制，2001，33（5）：531－535.

WANG Xuesong，CHENG Yuhu.A neural network-based predictive control system with temporal differences method［J］.Information and Control，2004，33（5）：531－535.

［18］CHANGC S，DU D.Further improvement of optimization method for mass transit signaling B lock-layout design using differential evolution［J］.IEEE Proceedings on Electric Power Applications，1999，146（5）：559－569.

［19］STORN R，PRICE K.Differential evolution——a simple and efficient adaptive scheme for global optimization over continuous spaces［R］.Berkeley：University of California，1995.

［20］朱光宇.模因内三角概率选择混合蛙跳算法［J］.计算机集成制造系统，2009，15（10）：1979－1985.

ZHU Guangyu.Meme triangular probability distribution shuffled frog-leaping algorithm［J］.Computer Integrated Manufacturing Systems，2009，15（10）：1979－1985.